Champ magnétique et forces de Laplace

Induction 1 Champ magnétique et forces de
Laplace
Lycée Polyvalent de Montbéliard - Physique-Chimie - TSI 1 - 2016-2017
Contenu du programme officiel :
Notions et contenus Capacités exigibles
Champ magnétique :
Sources de champ magnétique ; cartes de champ ma-
gnétique.
- Exploiter une représentation graphique d’un champ vectoriel, identifier les
zones de champ uniforme, de champ faible, et l’emplacement des sources.
- Identifier l’allure des cartes de champs magnétiques pour un aimant droit,
une spire circulaire et une bobine longue.
- Décrire un dispositif permettant de réaliser un champ magnétique quasi
uniforme.
- Citer des ordres de grandeur de champs magnétiques : au voisinage d’ai-
mants, dans une machine électrique, dans un appareil d’IRM, dans le cas
du champ magnétique terrestre.
Lien entre le champ magnétique et l’intensité du cou-
rant.
- Évaluer l’ordre de grandeur d’un champ magnétique à partir d’expressions
fournies.
Moment magnétique. - Définir le moment magnétique associé à une boucle de courant plane.
- Par analogie avec une boucle de courant, associer à un aimant un moment
magnétique.
Forces de Laplace :
Résultante et puissance des forces de Laplace s’exerçant
sur une barre conductrice en translation rectiligne sur
deux rails parallèles (rails de Laplace) dans un champ
magnétique extérieur uniforme, stationnaire et ortho-
gonal à la barre.
- Différencier le champ magnétique extérieur subi du champ magnétique
propre créé par le courant filiforme.
- Établir et connaître l’expression de la résultante des forces de Laplace
dans le cas d’une barre conductrice placée dans un champ magnétique
extérieur uniforme et stationnaire.
- Évaluer la puissance des forces de Laplace.
Couple et puissance des actions mécaniques de Laplace
dans le cas d’une spire rectangulaire, parcourue par un
courant, en rotation autour d’un axe de symétrie de la
spire passant par les deux milieux de cotés opposés et
placée dans un champ magnétique extérieur uniforme
et stationnaire orthogonal à l’axe.
- Établir et connaître l’expression du moment du couple subi en fonction
du champ magnétique extérieur et du moment magnétique de la spire
rectangulaire.
Action d’un champ magnétique extérieur uniforme sur
un aimant.
Positions d’équilibre et stabilité.
-Mettre en œuvre un dispositif expérimental pour étudier l’ac-
tion d’un champ magnétique uniforme sur une boussole.
Création d’un mouvement circulaire - Mettre en mouvement de rotation une aiguille aimantée grâce
au champ magnétique créé par plusieurs bobines.
En gras les points devant faire l’objet d’une approche expérimentale.
Table des matières
1 Le champ magnétique 2
1.1 Introduction au magnétisme. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Les cartes de champs magnétique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.3 Les courants électriques et le champ magnétique . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.4 Les moments magnétiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
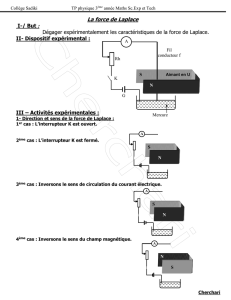
2 La force de Laplace 6
2.1 Mise en évidence expérimentale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.2 Résultante de la force de Laplace. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.3 Puissance de la force de Laplace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3 Couple des actions mécaniques de Laplace 8
3.1 Présentation............................................... 8
3.2 Calcul de la force de Laplace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3.3 Calcul du moment du couple de Laplace. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4 Action d’un champ magnétique sur un aimant 9
4.1 Champ magnétique extérieur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4.2 Champ magnétique tournant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Maxime Champion - www.mchampion.fr 1/10

Induction 1 : Champ magnétique et forces de Laplace Maxime Champion
1 Le champ magnétique
1.1 Introduction au magnétisme
Dès l’antiquité, les hommes remarquent qu’un minerai naturel, appelé « magnétite » (essentiellement de
l’oxyde de fer), a la propriété d’attirer de petits morceaux de fer. Cette interaction est appelée magnétisme,
les solides capables d’attraction magnétique étant appelés aimants.
ILes aimants
Expérience 1 : Interactions entre des aimants, interaction entre un aimant et de la limaille
de fer.
On constate que les aimants, quelle que soit leur forme et leur taille, sont polarisés. C’est-à-dire qu’il
possède un pôle Nord et un pôle Sud. Si un aimant est brisé, chacun des éclats aura à nouveau deux pôles.
On observe que
le pôle Nord d’un aimant et le pôle Sud d’un autre aimant s’attirent ;
les deux pôles de même polarité de deux aimants se repoussent.
Plus particulièrement, si on dispose de la limaille de fer, c’est-à-dire de minuscule bout de fil de fer,
autour d’un aimant, ils se disposent selon une géométrie particulière (figure 1a). Les copeaux de fer semblent
former une ligne continu allant d’un pôle à un autre. Si on remplace la limaille par un ensemble de petits
aimants (des boussoles), on remarque de plus que ceux-ci s’orientent dans la même direction le long d’une
ligne (figure 1b).
(a) Alignement de la limaille de fer autour d’un aimant. (b) Organisation de boussoles autour d’un aimant.
Fig. 1 – Photographie de l’alignement de limaille de fer et de boussoles autour d’un aimant.
Définition. Les lignes formées par la limaille sont appelées lignes de champ. Ces lignes sont orientées
par l’orientation des boussoles. On définit, pour le moment, le champ magnétique comme une grandeur
vectorielle tangente aux lignes de champ. Il se note #” Bet son unité est le Tesla (T).
IEffets magnétiques d’un courant électrique
Expérience 2 : Effet d’un courant parcourant un circuit sur un aimant
On remarque que l’orientation de l’aimant change en présence d’un circuit électrique parcouru par
un courant. Cela signifie que la présence d’un courant provoque l’apparition d’un champ magnétique. Au
même titre que les aimants, les circuits électriques parcourus par un courant sont des sources de champ
magnétique.
IOrdres de grandeurs de champs magnétiques
Champ... Ordre de grandeur
Bmagnétique terrestre ≈5×10−5T
Bcréé une bobine de 1000 spires parcourue par un courant de 1 A ≈10 mT
Bcréé par un aimant ≈0.1à1 T
Bdans un moteur électrique ≈0.5 T
Bcréé par un électroaimant ≈1à10 T
Bcréé par un appareil IRM ≈5 T
2/10

Induction 1 : Champ magnétique et forces de Laplace Maxime Champion
1.2 Les cartes de champs magnétique
Une carte de champ magnétique est une représentation schématique de la disposition de la photo-
graphie de la figure 1. Les différentes topographie du champ sont manipulables sur cette page internet
(animation [1]).
IQuelques cartes à reconnaître
Les trois cartes de champs suivantes de la figure 2 sont à reconnaître.
S N
(a) Carte de champ magnétique d’un aimant droit. Le champ est orienté du nord vers le sud.
i > 0
(b) Carte de champ magnétique créé par une boucle de courant. Le champ est orienté selon la
règle de la main droite (les doigts suivent le sens du courant et le pouce indique la direction du
champ magnétique).
i > 0
(c) Carte de champ magnétique créé par un solénoïde (c’est-à-dire un ensemble de spires les unes
contre les autres, autrement dit une bobine ou inductance). Le champ est orienté selon la règle de
la main droite.
Fig. 2 – Trois cartes de champs magnétique à reconnaître.
3/10

Induction 1 : Champ magnétique et forces de Laplace Maxime Champion
ILes propriétés des lignes de champ magnétiques
Propriété.
Les lignes de champs sont dirigé du pôle Nord vers le pôle Sud des aimants.
Si deux lignes de champ se coupent en un point, alors le champ est nul en ce point.
Si les lignes de champ sont parallèles entre elles et régulièrement espacées alors le champ est uniforme.
Les lignes de champ sont toujours des courbes fermées (dans un aimant, les lignes de champ se bouclent
à l’intérieur de l’aimant).
Les boucles de champ enroulent les courants électriques en respectant la règle de la main droite.
Lorsque les lignes de champ se resserrent, la norme de Baugmente. Les zones où le champ est le plus
intense se trouvent au voisinage de la source du champ magnétique.
Remarque : Les lignes de champs vont du pôle Nord vers le pôle Sud et les boussoles s’orientent
le long des lignes de champs. Cela est compatible avec la situation de la Terre, car les pôles
magnétiques et géographiques sont inversés.
Application 1 : Sur la carte de champ ci-dessous, identifier la direction des courants, les zones de
champs forts et les zones de champ faible.
IDeux dispositifs pour créer des champs magnétiques uniformes
On rappelle que le champ magnétique est uniforme, autrement dit qu’il ne dépend pas de la position,
si les lignes de champs sont parallèles. C’est le cas, entre autre, pour certaines zones de trois dispositifs :
à l’intérieur d’un solénoïde (figure 2c) ;
entre les deux branches de l’aimant en U (figure 3a) ;
4/10

Induction 1 : Champ magnétique et forces de Laplace Maxime Champion
entre deux bobines de Helmholtz (figure 3b). Il s’agit simplement de deux bobines fines mises en regard
l’une de l’autre avec le courant les parcourant dans le même sens.
(a) Entre les deux branches d’un aimant en U. (b) Entre les bobines de Helmholtz.
Fig. 3 – Dispositifs pour créer des champs uniforme.
1.3 Les courants électriques et le champ magnétique
Propriété. Toutes les charges électriques en mouvement rayonnent un champ magnétique. En particulier,
les électrons en mouvement dans un courant électriques sont responsables de l’apparition d’un champ
magnétique.
Les expressions mathématiques du champ magnétique en fonction de la forme des circuits électriques
seront étudiées pour certains cas en deuxième année. On retiendra que, dimensionnellement parlant, on a
B∝µ0I
L
avec Ile courant électrique responsable du champ magnétique, Lune distance typique du problème et
µ0= 4π×10−7H/mla perméabilité magnétique du vide.
Application 2 : Le champ magnétique uniforme à l’intérieur d’un solénoïde de N= 1000 spires,
de longueur L= 10 cm et parcouru par un courant i= 0.1 A est donné par B=µ0N
Li. Que vaut le
champ magnétique en Tesla ?
1.4 Les moments magnétiques
IMoment magnétique d’une boucle de courant
Définition. On considère une spire de rayon Rparcourue par un courant i. Cette boucle forme une surface
S. La normale à la surface est notée #” n. Il s’agit d’un vecteur unitaire, normal à la surface formée par la
boucle de courant et orienté dans le sens de la main droite (défini à partir du sens du courant). On définit
le vecteur surface #” S=S#” n.
Le moment magnétique
# ”
Mde la spire plane (en A·m2) est :
# ”
M=i#” S=iπR2#” n . (1.1)
Vecteur surface #” S=S#” nsurface S=π R2
Boucle de courant
i
5/10