ELCINQ_03 Loi des noeuds en termes de potentiels en alternatif et

G.P. Questions de cours électrocinétique
Loi des nœuds en termes de potentiels en sinusoïdal et généralisation:
Retrouver les expressions des admittances complexes en sinusoïdal .
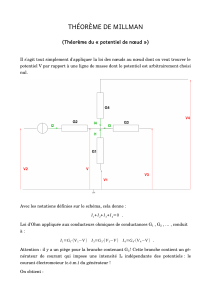
En appliquant la méthode proposée (cf. théorème de Millman) au circuit suivant, écrire les
équations permettant d'obtenir
v
et
v '
.
Généraliser la méthode pour déterminer
vt
et
v ' t
en régime variable quelconque.
Réponse:
Admittances:
En convention récepteur:
pour une résistance:
u=R i
u=R i
i=1
Ru
donc
Y=G=1
R
pour une bobine idéale:
u=Ld i
d t
u=j L i
i=u
j L 
donc
Y=1
j L 
pour un condensateur idéal:
i=Cd u
d t
v' v
R
I max cos(ωt)
R
C
C
R
E max cos(ωt)
R
L
L

G.P. Questions de cours électrocinétique
i=j C u
donc
Y=j C 
Loi des nœuds en termes de potentiels en sinusoïdal:
La somme des intensités arrivant à un nœud est nulle.
1) nœud de potentiel
v '
:
t 1
R1
jC 
0– v '  jC 0– v '  1
Rv – v ' =0
2) nœud de potentiel
v
:
1
Rv ' – v 1 jL0– v  1 RjL 0– v 1 REmax exp jt– v =0
(pour le dernier terme, je fais comme si l'ordre du générateur
de tension et de la résistance étaient inversés dans la branche)
D'où les deux équations à deux inconnues
v
et
v '
.
Généralisation:
Ce circuit à deux nœuds et une masse, où l'on cherche des potentiels est intéressant à résoudre par
la même méthode.
On doit provisoirement introduire deux « nœuds virtuels » supplémentaires (voir suite)
1) nœud de potentiel
v ' t
:
tCd
dt v '1t−v ' tCd dt 0−v ' t 1 Rvt– v ' t=0
équation (1)
2) « nœud » de potentiel
v1't
:
1
R0−v1'tCd dt v ' t−v1't=0
équation (2)
v'(t) v(t)
R
η(t)
R
C
C
R
e(t)
R
L
L
v1'(t) v1(t)

G.P. Questions de cours électrocinétique
3) nœud de potentiel
vt
:
1
Rv ' t– v tiLiLR1 Ret– v t=0
avec
iL
et
iLR
, orientés vers ce nœud, donnés
par:
0−vt=LdiL
dt
v1t−vt=LdiLR
dt
On doit donc dériver l'équation de départ pour éliminer les intensités
iL
et
iLR
:
1
R
d
dt v ' t– v t 1 L0−vt 1 Lv1t−vt 1 R
d
dt et– v t=0
équation (3)
4) « nœud »de potentiel
v1t
:
1
R0−v1t−iLR=0
On doit dériver l'équation de départ:
1
R
d
dt 0−v1t 1 Lvt−v1t=0
équation (4)
Il faudrait alors dans le cadre de cette méthode systématique résoudre le système des quatre
équations différentielles du premier ordre (voir cours de maths).
En partant de l'étude en sinusoïdal, en faisant passer tous les
p=j
au numérateur puis en les
transformant en
pd
dt
on obtenait directement un système de deux équations différentielles du
second ordre.