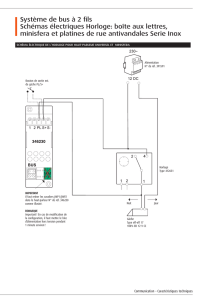
Le temps dépend du référentiel d`étude.

1
TERMINALE S
TEMPS ET RELATIVITE
RESTREINTE
A) Invariance de la vitesse de la lumière dans le vide.
1) Énoncés des postulats.
►Postulat 1 :
Les lois de la physique s’expriment de la même façon dans tous les
référentiels galiléens.
►Postulat 2 : Postulat d’invariance de la vitesse de la lumière
La célérité de la lumière dans le vide est une CONSTANTE UNIVERSELLE.
La vitesse de la lumière c est CONSTANTE dans tous les référentiels galiléens.
Elle ne dépend pas de la vitesse de la source, ni de celle de celle de l’observateur.
Remarque :
La lumière se propage avec la même célérité c =299792458 m.s-1 soit environ
3,00× 10 8 m.s−1 dans le vide, quel que soit le référentiel d'étude.
►Conséquences :
- Il existe une vitesse limite, égale à la célérité c de la lumière dans le vide.
- Cette vitesse limite ne peut être dépassée par aucun et signal et aucune
particule.
2) La relativité restreinte.
a)- Notion d’évènement :
Un évènement est un phénomène objectif observable, c’est un fait se
produisant à un endroit donné.
Pour repérer un évènement, il faut choisir un référentiel et lui attribuer des
coordonnées spatio-temporelle (x, y, z, t).
Exemple d’évènement : un éclair, une explosion, l’aiguille d’une horloge qui
coïncide avec l’indication du cadran, impulsion lumineuse, …
b)- Temps et durée
Le temps est une grandeur mesurée par une horloge. ( chronomètre , montre)
►Cas de la physique classique (Newton).
- Le temps est absolu. Il est le même dans tout le référentiel et quelques
soient les conditions extérieures.
►Cas de la relativité restreinte (Einstein).
- Le temps dépend du référentiel d’étude.

2
- Le temps ne s’écoule pas de la même façon pour tout observateur.
- La durée séparant deux évènements dépend du référentiel d’étude.
La relativité restreinte se manifeste lorsqu’il y a mouvement relatif à des
vitesses proches de la vitesse de la lumière dans le vide C.
On considère que le référentiel A se déplace à la vitesse par rapport au
référentiel B. Une horloge en mouvement et une horloge fixe ne mesurent pas
les mêmes durées entre les évènements 1et 2.
Dans le référentiel A :
Schéma :
Dans le référentiel B, l’observateur B est immobile ( sol) et voit le référentiel A (et
l’horloge) se déplacer à la vitesse
Schéma :

3
À l’aller, le signal arrive sur le miroir au bout de la durée 1 et met la durée 2
pour le retour.
Pendant la durée 1, l’ensemble s’est déplacé de la distance (v . 1)
En utilisant Pythagore, on peut écrire que :
(c . 1)2 = d2 + (v . 1)2
De même pour le retour, on écrit :
(c . 2)2 = d2 + (v . 2)2
On tire de ces expressions :
En conséquence :
Les durées sont telles que ΔtB ≠ ΔtA
- On peut calculer le rapport ΔtB / ΔtA
On appelle  le coefficient de Lorentz le coefficient  ≥ 1
On remarque que : ΔtB ≥ ΔtA
Le temps s’écoule plus vite dans le référentiel A qui est en mouvement et plus
lentement dans le référentiel B.
c)- Notion de temps propre ou durée propre
La durée propre ΔT0, est la durée séparant deux évènements mesurée par une
horloge fixe ayant lieu au même point dans un référentiel galiléen (R).
Cette durée propre ΔT0 est mesurée par une horloge fixe, proche des deux
évènements dans le référentiel (R).
On utilise les termes de « temps propre » ou « durée propre » (on préfère le
terme « durée propre »).

4
d)- Temps mesuré ou durée mesurée.( temps ou durée impropre)
La durée mesurée ΔT’ est la durée séparant deux évènements mesurée par une
horloge ayant lieu en deux points distincts dans un référentiel galiléen (R’) en
mouvement par rapport au référentiel galiléen (R).
f)- Relativité du temps.
Les durées ΔT’ et ΔT0 sont liées par la relation de dilatation temporelle :
ΔT’ = . ΔT0
Le coefficient γ (gamma), sans unité, est donné par la relation :
γ : grandeur sans unité, γ ≥ 1
v : valeur de la vitesse relative d’une horloge par rapport à
l’autre, unité : m / s
c : valeur de la vitesse de la lumière dans le vide : unité : m / s.
Remarques :
- Deux horloges en mouvement relatif ne mesurent pas la même durée entre
deux évènements ΔT’ ≥ ΔT0
- C’est le phénomène de dilatation des durées.
- Une horloge qui se déplace par rapport à un observateur bat plus lentement
qu’une horloge immobile par rapport à l’observateur.
g)- Application :
On considère une sonde spatiale se déplaçant à la vitesse v = 1,0 x 105 m / s
par rapport à un référentiel terrestre supposé galiléen.
- Quel est l’écart relatif entre la durée propre et la durée mesurée
dans le référentiel terrestre.
- Réponse :
- ΔT’ ≥ ΔT0

5
- Lorsque la vitesse v << c, la dilatation de temps est imperceptible.
1) Vérification expérimentale de l’invariance
Cette expérience consiste à mesurer, à l’aide de leur temps de vol sur des distances
d’environ 80 mètres, la vitesse de photons produit par la désintégration d’une particule
appelé méson 𝜋0
Dans cette expérience, une particule le méson 𝝅0, animée d’une vitesse égal à
0,9975c, se désintègre en deux photons 𝜸 qui partent dans des sens opposés à la
même vitesse c par rapport au méson 𝜋0 (référentiel R’ en translation uniforme).
Dans le référentiel du laboratoire, le photon émis dans le sens du mouvement du méson
𝜋0 devrait avoir une vitesse de …………….,
celui émis dans le sens opposé devrait avoir une vitesse pratiquement nulle
(……………..).
L’expérience montre que les deux photons atteignent au bout de la même durée Δt les
détecteurs.
La vitesse expérimentale de chaque photon est donc ……………. ; l’expérience a donné
une vitesse égale à c pour chacun des photons.
Application.
1)- La localisation par GPS.
a)- Les satellites de localisation GPS.
Le GPS (Global Position Système) comprend un ensemble de 24 satellites.
Chaque satellite embarque une horloge atomique de haute précision et évolue sur
une orbite circulaire autour de la Terre.
Il émet régulièrement un signal électromagnétique indiquant la date d’émission et sa
position par rapport à la Terre.
Le GPS situé dans une voiture (par exemple) détecte la date d’arrivée du signal.
-Avec ces deux informations, date d’arrivée et date d’émission, le récepteur calcule la
durée de propagation du signal et en déduit la distance qui le sépare du satellite.
Détecteur
Dét
ect
eur
Méson 𝛑𝟎
Photon 2
𝐏𝟐
⃗
⃗
⃗
⃗
𝐏𝟏
⃗
⃗
⃗
⃗
Pméson
P
méson
𝐏𝟐
⃗
⃗
⃗
⃗
Détecteur