ne pas confondre vitesse et precipitation

NE PAS CONFONDRE VITESSE ET PRECIPITATION
-----------------------------------------------------------------------
Cette expression est celle d’un vieux proverbe français très populaire et très connu, qui
suggère que, sous prétexte de vouloir accélérer un mouvement déjà assez rapide, on
court le risque de tout gâcher.
Ce proverbe plein de bon-sens fait donc le distingo entre la vitesse d’un objet et le
renforcement instantané de cette vitesse, donc l’accélération, dont on veut faire béné-
ficier l’objet.
On se doute alors que, si l’on veut transcrire cette situation en termes mathématiques,
Il va falloir exprimer différemment les termes de vitesse et d’accélération.
La vitesse est l’expression du mouvement d’un objet dans un référentiel….de référence !
Ainsi, la carafe posée sur la table semble totalement immobile par rapport à celle-ci. Mais
elle se déplace à la vitesse de 1666 km/h si le référentiel devient la Terre ; à 30 km/sec
dans le mouvement terrestre autour du Soleil ; à 250 km/sec dans le mouvement galacti-
que du Soleil. Je vous fais grâce de la constante de Hubble…
C’est la raison pour laquelle Galilée a parlé le premier de Relativité, à juste raison donc.
En termes mathématiques, la vitesse est exprimée depuis Képler par une formule :
V² = GMo / R ,
où, historiquement, outre le carré de la vitesse d’une planète autour du Soleil de masse Mo,
on retenait la distance R entre la planète et le Soleil et bien sûr la constante gravitationnelle G.
Donc, pour une série de planètes situées à R1 , R2 , R3 etc…on pouvait écrire :
V1² = GMo / R1 ; V2² = GMo / R2 ; V3² = GMo / R3 ; etc…
Ou encore : R1 V1² = R2 V2² = R3 V3² = GMo.
Certains ont appelé, de manière courante mais abusive, GMo une « constante ».
(1)

L’idée était de tenir compte du fait que, dans les lois de Képler, la référence est le Soleil, dont
la masse est pratiquement constante, l’accroissement de masse globale de Mercure jusqu’à
Pluton étant négligeable par comparaison. Les planètes sont même comparées à des
« particules ».
Nous voyons alors que la formule de l’égalité des produits distance-vitesse² égale à GMo
implique que GMo est constant, et doit le demeurer. En conséquence, on ne peut admettre
la moindre addition SIGNIFICATIVE de masse à GMo sans rompre l’égalité. Autrement dit :
pas question d’ajouter de la matière noire entre le Soleil et sa dernière planète !!
Nous verrons plus tard que la situation est totalement différente dans la Voie Lactée.
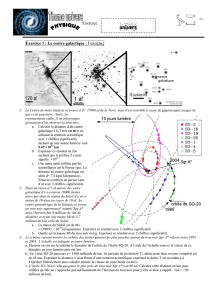
La formule de Képler donne sur un graphique avec la vitesse² en ordonnées et la distance en
abcisses, une magnifique hyperbole de type y = GMo / x, valable dans le système solaire.
C’est donc cette hyperbole que les astronomes attendaient en mesurant les vitesses stellaires
dans les galaxies spirales dont la Voie Lactée, appliquant à celles-ci la troisième loi de Képler.
Quelle ne fut pas leur surprise de constater que la courbe était strictement plate !!
Or, au lieu de se remettre en question et de se demander s’ils n’avaient pas commis une erreur
quelque part, ils ont déclaré que la seule manière d’expliquer cette courbe était d’ajouter de la
matière, invisible mais active au plan gravitationnel, qu’ils ont appelée « matière noire »
D’où vient l’erreur ?
La formule de la vitesse V² n’a pas été utilisée dans les calculs, mais celle de la force de
Newton.
Or, si la vitesse s’exprime en GMo / R, la force de Newton tient compte de l’accélération, soit
la dérivée de la vitesses. Cette accélération s’écrit :
V² / R = GMo / R² = γ ( g pour l’accélération terrestre ).
D’où la formule de Newton : F = GMMo / R² peut s’écrire F = M. GMo / R² = M. γ
(2)

Soit la seconde loi de Newton : on dit qu’une force F s’exerce sur un objet M lorsqu ‘elle a une
influence, soit sur sa vitesse, soit sur sa direction grâce à son accélération γ.
Or, l’égalité mesurée l’a été sur les vitesses et non les forces. La formule à utiliser est donc :
V² = GM / R , avec : R = point où la mesure sera effectuée.
M = masse intervenant au point de mesure R.
V² est aussi appelé potentiel gravitationnel de GM en R.
Ainsi, le long d’un rayon galactique de 50.000 AL, on situe des points de mesure R1 ,R2 ,R3….
Si on appelle les masses situées entre le centre galactique et le point de mesure M1 ,M2 ,M3
etc… on écrira l’égalité des vitesses :
V² = GM1 / R1 = GM2 / R2 = GM3 / R3 etc…
Ainsi, si par exemple R2 = 2 R1 et R3 = 3 R1 alors :
GM2 = 2 GM1 et GM3 = 3 GM1 : la masse galactique est également répartie sur l’axe de son
rayon . Rien à voir avec la masse unique, centrale du Soleil !!!
Si on trace le schéma de cette galaxie, on obtient l’image typique d’une galaxie spirale vue par
la tranche.
En prenant pour valeurs de référence la vitesse terrestre VT² = (30 km)² / sec²
Mo la masse du Soleil et RT la distance Terre-Soleil ( 150.106 km = 150.109 m ), d’une part ;
MG(S) la masse galactique à la position du Soleil (3 / 5 de la masse galactique totale) et
RG(S) la position du Soleil ( 3 / 5 du Rayon soit 30.000 AL)
V² comme vitesse commune à toutes les étoiles = (250 km)² / sec² , d’autre part ; On a :
30² = GMo / RT et 250² = GMG(S) / RG(S)
Ce qui donne MG(S) = 141.109 Mo ; et pour la totalité de la Voie Lactée :
MG = 141.109 Mo x 5 / 3 = 235.109 Mo…sans une trace de matière noire !!!
L’erreur de confondre vitesse et accélération (ou force) a été involontairement contournée par
(3)

Milgrom qui, en prétendant que la loi de force de Newton se modifiait à grande échelle en
prenant l’allure GM / R, n’a fait que rectifier le tir, mais comme Monsieur Jourdain : sans le
savoir.
La manière classique de résolution du problème peut être soutenue par une extrapolation : je
veux parler des trous noirs.
La fameuse formule de Scharzschild donne la taille du rayon RS mesuré à l’horizon du trou noir,
soit le point où la vitesse de libération est égale à celle de la lumière :
RS = GM / C² ; soit : C² = GM / RS.
Nous voyons donc immédiatement que GM et RS sont dans une équation de type y = a x ( qui
est une droite ) qui s’écrit GM = C² RS , où :
-y est représenté par GM.
-a est représenté par la constante C² ( c’est la pente de la droite )
-x est représenté par RS
On peut donc écrire, pour des trous noirs de masses croissantes M1 , M2 et M3 :
C² = GM1 / RS1 = GM2 / RS2 = GM3 / RS3
Or, les trous noirs ne sont que des cas particuliers de la gravitation, mais qui obéissent aux lois
au même titre qu’une étoile . En remplaçant C² par la vitesse galactique V², on voit que la
matière dans les galaxies spirales est en rapport avec la position de l’étoile considérée sur le
rayon : la masse galactique augmente proportionnellement à la distance au centre galactique.
En construisant la figure, on obtient une magnifique galaxie spirale de profil.
Ainsi, nous voyons qu’une galaxie spirale se contente de sa forme et de sa masse pour expli-
quer la constatation de l’égalité des vitesses des étoiles qui la composent.
Pour tout complément d’information, se référer au site :
http//www.fractaledelunivers.net.
(4)

Structure de galaxie spirale de profil obtenue par égalité des vitesses stellaires.
La droite GM = C²Rs est un cas particulier de GM = V²R. Elle a le mérite de montrer la relation
linéaire entre GM et R quand la vitesse est constante, ce qui est le cas des trous noirs.
Vo² est la vitesse à la surface du soleil Mo ; V1² et V2² sont les vitesses aux distances R1 et R2
(3° loi de Képler) La vitesse stellaire constante dans la galaxie signe la proportionnalité
Masse-Rayon dont le rapport reste constant, égal à V² = ( 250km )² / sec²
( 5 )