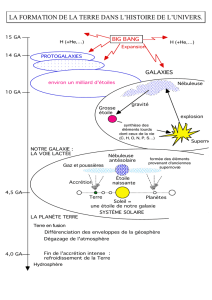
univers

Exercice
Exercice I : Le centre galactique : Γαλαξίας
1- Le Centre de notre Galaxie se trouve à d= 27800 al de la Terre, mais il est invisible à cause de gigantesques nuages de
gaz et de poussière . Seuls, les
rayonnements radio, X ou infrarouges
permettent d’en observer la structure.
a. Calculer la distance d du centre
galactique à la Terre en m et en
utilisant la notation scientifique
avec 3 chiffres significatifs
sachant qu’une année lumière vaut
9.47 ×1012 km
b. Exprimer ce résultat en Zm
sachant que le préfixe Z (zeta)
signifie ×1021
c. Une autre unité utilisée par les
scientifiques est le Parsec (pc). La
distance au centre galactique est
alors d= 7.6 kpc( kiloparsecs).
Trouver combien un parsec vaut
d’al avec 2 chiffres significatifs
2- Dans un rayon d’1 al autour du centre
galactique il y a environ 10000 étoiles
alors que dans la région du Soleil il y en a
moins de 10 dans un rayon de 10 al. Au
centre géométrique de la Galaxie se trouve
un trou noir supermassif nommé Sgr A*
dont l’horizon fait 6 millions de km de
diamètre et ayant une masse Mt de 3.7
millions de fois celle du Soleil.
a. La masse du Soleil est de Ms
=1,98892 × 1030 kilogrammes. Exprimer ce résultat avec 2 chiffres significatifs
b. Quelle est la masse Mt du trou noir en kg. Exprimer ce résultat avec 2 chiffres significatifs.
3- Le schéma suivant montre les orbites des étoiles géantes les plus proches autour du trou noir Sgr A* relevés entre 1995
et 2004. L’échelle est indiquée en jours-lumière.
a. Mesurer en cm sur le schéma le diamètre de l’orbite de l’étoile SO-20. A l’aide de l’échelle trouver la valeur de ce
diamètre en jour lumière puis en km
b. En 1 tour SO-20 parcours x= 1400 milliards de km. Sa période de révolution T ( durée pour faire un tour complet) est
de 43 ans. Exprimer la distance x sous forme d’une notation scientifique, exprimer la durée T en secondes (s) .
Exprimer littéralement puis calculer ensuite la vitesse de cette étoile en km/s
c. L’étoile SO-16 est celle qui passe le plus près du trou noir Sgr A* soit 90 ua. Calculer cette distance en km pour
vérifier qu’elle ne s’approche pas suffisamment de l’horizon du trou noir pour y être avalée. ( rappel : 1ua = 150
millions de km).
univers

EXERCICE II VOIR LOIN
1- Pourquoi voit-on le passé quand on
regarde les étoiles
2- Le soleil se trouve à 150 millions de km.
Combien de temps met sa lumière pour
parvenir jusqu’à nous. Même question
pour la lune située à 400 000 km.
3- La galaxie d’Andromède est un des
objets les plus lointains que l’on peut
voir à l’œil nu sous forme d’une tache
floue. Elle se trouve à 2.5 Mal (millions
d’années-lumière) combien de temps
met sa lumière pour parvenir jusqu’à
nous. A quelle distance se trouve-t-elle
en km ?
4- Le soleil se trouve à 27800 al du centre galactique. A l’aide du schéma
ci-dessous trouver le diamètre de la Galaxie
5- La nébuleuse d'Orion se trouve à 1,70 x 1016 km de la Terre.
a. A quelle distance, en année de lumière, la nébuleuse d'Orion
M42 se trouve-t-elle de la Terre ?
b. Fait-elle partie notre galaxie ?
c. A quelle époque se trouvait-on sur Terre quand a été émise la
lumière qui nous parvient aujourd'hui de cette nébuleuse ?