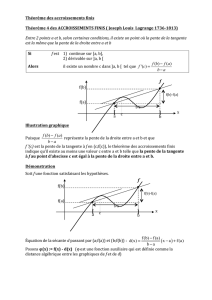
Inégalité des accroissements finis. Exemples

f g
[a, b] ]a, b[t]a, b[f0(t)≤g0(t)
f(b)−f(a)≤g(b)−g(a).
h=g−f[a, b] ]a, b[
c∈]a, b[h(b)−h(a)=(b−a)h0(c)h0(c)≥0
h(b)−h(a)≥0f(b)−f(a)≤g(b)−g(a)
f[a, b] ]a, b[
α β t ]a, b[α≤f0(t)≤β
α(b−a)≤f(b)−f(a)≤β(b−a).
f g [a, b] ]a, b[t
]a, b[|f0(t)| ≤ g0(t)
|f(b)−f(a)| ≤ g(b)−g(a).
f[a, b] ]a, b[M
t]a, b[|f0(t)| ≤ M
|f(b)−f(a)| ≤ M(b−a).
g g(t) = βt
−f
|f(b)−f(a)| ≤ g(b)−g(a)−g(b) + g(a)≤f(b)−f(a)≤g(b)−g(a)
f−f
α=−M β =M g(t) = Mt 

f[a, b] ]a, b[f0
]a, b[f m = inf]a,b[f0
M= sup]a,b[f0f
y=f(a) + M(x−a)y=f(b) + M(x−b)y=f(a) + m(x−a)y=f(b) + m(x−b)
√401
[400,401] 1
2√401 ≤√401 −√400 ≤1 2√400 (20.025)2>401
20 + 100
4005 ≤√401 ≤20 + 100 4000
cos
x > 0
−1≤cos x≤1⇒ −x≤sin x≤x⇒ −x2
2≤1−cos x≤x2 2⇒. . .
f]a, b[
f]a, b[f0]a, b[
f]a, b[f0]a, b[
f]a, b[f0]a, b[
x0∈]a, b[f]a, b[x∈]x0, b[f(x)−f(x0)
x−x0≥0x x0
f0(x0)≥0f]a, b[
t∈]a, b[f0(t)≥0x<y ]a, b[
f(y)−f(x)≥0f]a, b[
f[a, b] ]a, b[ lim
x→a+f0(x) = l f0
d(a)
f a l
∀ε > 0∃hε:a<x<a+hε⇒l−ε≤f0(x)≤l+ε.
f[a, x]
l−ε≤f(x)−f(a)
x−a≤l+ε

∀ε > 0∃hε:a<x<a+hε⇒
f(x)−f(a)
x−a−l
≤ε
lim
x→a+
f(x)−f(a)
x−a=l=f0
d(a)
a f
]a, b[
lim
x→a+f0(x) = +∞ −∞ a+∞
−∞ fR∗f(x) = x2sin( 1
x2) 0 f(0) = 0
Rf0(0) = lim
x→0
f(x)
x= 0 ∀x6= 0 f0(x) = 2xsin( 1 x)−cos( 1 x)x
0
I x0I f I
I\ {x0}lim
x→x0
f0(x) = l f0x0f0(x0) = l
fCn[a, b]f(n+1) ]a, b[M
t∈]a, b[|f(n+1)(t)| ≤ M
f(b)−f(a)−
n
X
k=1
(b−a)k
k!f(k)(a)
≤(b−a)n+1
(n+ 1)! M.
h
h(t) = f(t)−f(a) +
n
X
k=1
(b−t)k
k!f(k)(t).
x > 0n
0< ex−
n
X
k=0
xk
k!≤xn+1 (n+ 1)!ex.
e∈R\Q
e=p
qp q
n≥q
0< n!(p
q−
n
X
k=0
1
k!)≤e n+ 1
n n ≥max(2, q)
Pn(x) = Pn
k=0
xk
k!
(Hn) : ∀x > 0,0< ex−Pn(x)≤xn+1
(n+ 1)!ex

exp ]0,+∞[ 0 < ex−P0(x)x > 0
t∈[0, x]et≤ex[0, x]ex−P0(x)≤xex
(H0)
(Hn) (Hn+1)hn(x) = ex−Pn(x)x
hn+1 R+h0
n+1 =hn(Hn)h0 n+1(t)>0t > 0hn+1
hn+1(x)> hn+1(0) x > 0hn+1(x)>0
(Hn) exp
∀t∈]0, x[, h0
n+1(t)≤tn+1
(n+ 1)!et≤tn+1 (n+ 1)!ex
hn+1(x)−hn+1(0) ≤xn+2
(n+ 2)!ex
(Hn+1)
(H0)n(Hn) (Hn+1) (Hn)n
f[a, b] [a, b] [a, b] ]a, b[
k∈[0,1[ x∈]a, b[|f0(x)| ≤ k
f[a, b]
un+1 =f(un)
u0∈[a, b].
g[a, b]g(x) = f(x)−x g
[a, b]g(a)≥0g(b)≤0l∈[a, b]g(l)=0
f(l) = l
l l0f l < l0
f[l, l0]|f(l)−f(l0)| ≤ k|l−l0|(1 −k)|l−l0| ≤ 0
1−k > 0l=l0
u0∈[a, b]f[a, b]⊂[a, b]
[a, b]unl
|un+1 −l|=|f(un)−f(l)| ≤ k|un−l|
|un−l| ≤ kn|u0−l|.
k∈[0,1[ limn→+∞kn= 0 (un)nl
√2
un+1 =un
2+1 un
u0= 1
f(x) = x
2+1 x[1,2]
f f

f
l
k= 1 f(x) = x
f: [1,+∞[→R+limx→+∞f(x) = 0 R+∞
1f(x)dx
+∞
P
n=1
f(n)
f x 7→ Rx
1f(t)dt f
t∈[n, n + 1] f(n+ 1) ≤f(t)≤f(n) [n, n + 1]
f(n+ 1) ≤Zn+1
n
f(t)dt ≤f(n)
−f(1) +
N
X
n=1
f(n)≤ZN
1
f(t)dt ≤ −f(N) +
N
X
n=1
f(n)
f
+∞
P
n=1
f(n)
lim
N→+∞
+N
P
n=1
f(n)=+∞R+∞
1f(x)dx lim
N→+∞RN
1f(x)dx = +∞
(un)nn≥1un=
2n
P
p=n+1
1
p
l= ln 2
f(t) = eit f(0) = 1 = f(2π)f0(t) = ieit [0,2π]
f g [a, b] ]a, b[f g
∀t∈]a, b[|f0(t)| ≤ g0(t).
|f(b)−f(a)| ≤ g(b)−g(a)
h[a, b]h(x) = Ref(x)−f(a)·f(b)−f(a)h
[a, b] ]a, b[
h0(x) = Ref0(x)·f(b)−f(a)|h0(x)| ≤ g0(x)|f(b)−f(a)|x∈]a, b[
h g |h(b)−h(a)| ≤ (g(b)−g(a))|f(b)−f(a)|
|f(b)−f(a)|2≤(g(b)−g(a))|f(b)−f(a)|f(b)−f(a) = 0
|f(b)−f(a)|