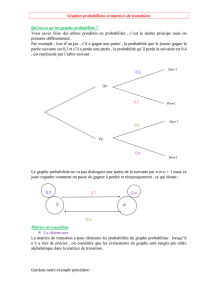
Graphes probabilistes

1
Séquence 4 – MA04
Graphes
probabilistes
Séquence 4
Sommaire
1. Pré-requis
2. Notion de graphe probabiliste
3. Synthèse de la séquence
4. Exercices de synthèse
 Étudier des phénomènes d’évolution simples.
 Modéliser, à l’aide d’un graphe probabiliste, un système à 2 ou 3 états pouvant évoluer aléatoirement au
cours du temps.
 Faire le lien avec les suites géométriques.
Objectifs
© Cned - Académie en ligne

2
Séquence 4 – MA04
1Pré-requis
Systèmes d’équations linéaires
à 2 ou 3 inconnues
On considère le système ()
S
de deux équations linéaires à 2 inconnues suivant
02 04
08 06
,,
,, .
xyx
xyy
+=
+=
 Mettre ce système sous la forme matricielle
xy ac
bd xy
()().
=
 Montrer que ce système se ramène à l’équation 2
x – y = 0.
 Résoudre le système ()
S
1 20
1
xy
xy
−=
+=
.
 Le système()
S
s’écrit
xy xy
()0,2 0,8
0,4 0,6 ().
=
 Résolvons le système ()
S
02 04
08 06
,,
,, .
xyx
xyy
+=
+=
Ce système s’écrit −+ =
−=
08 04 0
08 04 0
,,
,, ,
xy
xy
ce qui se ramène à la seule équation
2 x – y = 0.
 Résolvons le système ()
S
1 20
1
1
1
1
2
xy
xy
−=
+=
−
On obtient 3
x = 1 et 3 y = 2. D’où
x =1
3 et
y =2
3.
L’ensemble des solutions du système ()
S
1 est l’ensemble 1
᏿ tel que
1
3;2 3.
1=
᏿
On considère le système ()
S
de trois équations linéaires à 3 inconnues suivant,
écrit sous forme matricielle:
xyz xyz
()
0,5 0,4 0,1
00,40,6
0,3 0,3 0,4
(). =
A
Exercice
Solution
Exercice
© Cned - Académie en ligne

3
Séquence 4 – MA04
 Montrer que ce système ()
S
se ramène au système de deux équations linéaires
à 3 inconnues suivant: 530
660
xz
xyz
−=
+−=
.
 Résoudre le système ()
S
2
530
660
1
xz
xyz
xyz
−=
+−=
++=
.
 Le système ()
S
s’écrit :
05 03
04 04 03
01 06 04
,,
,,,
,, ,
xzx
xyzy
xyzz
+=
++=
++=
 , soit
xz
xyz
xyz
L
L
L
0,5 0,3 0
0,4 0,6 0,3 0
0,1 0,6 0,6 0
1
2
3
−+=
−+=
+−=
On a
LL L .
23 1
+=− On peut donc supprimer l’une des trois équations, par
exemple
L
2 (au vu de l’énoncé).
Il reste alors −+=
+−=
05 03 0
01 06 06 0
,,
,, , ,
xz
xyz
ce qui s’écrit aussi 530
660
xz
xyz
−=
+−=
.
 Résolvons le système ()
S
2
530
660
1
1
6
xz
xyz
xyz
−=
+−=
++=
−
Méthode 1
On élimine l’inconnue y entre les deux dernières équations pour obtenir un sys-
tème à 2 inconnues, x et z .
On obtient 5 x + 12 z = 6.
Résolvons le nouveau système de deux équations à 2 inconnues
530
5126
1
1
xz
xz
−=
+=
−
On obtient 15
z = 6 d’où
z =2
5. On en déduit
xz
3
5
3
5
2
5
6
25
==×= et
yxz =− − =− − =11
6
25
2
5
9
25.
L’ensemble des solutions du système ()
S
2 est l’ensemble 2
᏿ tel que
6
25 ;9 25 ;2 5.
2=
᏿
Méthode 2
Posons
Xxyz =
,
A =
−−
511
061
361
et
B [0 0 1].=
L’écriture matricielle du système est
XAB .×=
Solution
© Cned - Académie en ligne

4
Séquence 4 – MA04
Écran 1 Écran 2
Comme
A est inversible, on a
XAA BA ,
11
×× =×
−−
soit
XBA
1
I×=×−, ce
qui donne
XBA .
1
=×−
La copie d’écran 2 nous donne
xy ==
6
25
9
25
, et z =2
5.
Dans la séquence 1, on avait comme disposition:
[matrice] vecteur
colonne
vecteur
colonne .×
=
Dans cette séquence 4, on adoptera:
[matrice ligne] × [matrice] = [matrice ligne].
Suivant la disposition, la matrice n’est pas la même.
Pour le système précédent, on aurait pu résoudre :
A
x
y
z
0
0
1
,
t
×
=
soit
x
y
z
50 3
16 6
11 1
0
0
1
.
−
−
×
=
Matrices carrées
On donne
M
0,9 0,1
0,4 0,6 ,=
N =
08 02
08 02
,,
,,
,
R =−
−
02 02
08 08
,,
,,
.
 Vérifier que
M = N + 0,5 R . Montrer que
NNRRNRRNO ;et .
22
= = ×=×=
 a. Exprimer les matrices
M
2 et
M
3 en fonction des matrices
N et R .
b. On admet que, pour tout entier naturel
n ≥1, MN R
nn
=+05,.
En déduire la valeur exacte de chaque coefficient de la matrice
Mn .
c. Déterminer la limite de chaque coefficient de la matrice
Mn
quand n tend
vers l’infini. Écrire la matrice L dont les coefficients sont les limites des coef-
ficients de la matrice
Mn .
 Vérifier que
M [0,8 0,2] [0,8 0,2].×=
La copie d’écran 1
nous montre que
A est inversible.
B
Exercice
© Cned - Académie en ligne

5
Séquence 4 – MA04
 On calcule
+=
+−
−
= 
+ −
−
=
NR 0,5 0,8 0,2
0,8 0,2 0,5 0,2 0,2 0,8 0,8
0,8 0,2
0,8 0,2
0,1 0,1
0,4 0,4
0,9 0,1
0,4 0,6 .
On a bien
M = N + 0,5 R .
Calculons
NRNRRN
22
,, et à la calculatrice.
On pose:
N = A
R = B .
NN
2=
RR
2=
NR RN O ==
 a. On a
MN R N NR RN R
222 2
05 05 05 025=+ =+++(,) ,,,
,
soit
MN R
2025=+,.
On a
MMMN RN RN NR RN R ( 0,25 )( 0,5 ) 0,5 0,25 0,125 ,
32 2 2
==+ +=+ + +
soit
MN R
30 125=+,.
b. On admet que, pour tout entier naturel
n ≥1, MN R
nn
=+05,.
D’où
M
0,8 0,2 0,5 0,2 0,2 0,5
0,8 0,8 0,5 0,2 0,8 0,5 .
nnn
nn
=+× −×
−× +×
c. Comme 0 < 0,5 < 1, lim , .
n
n
→+∞ =05 0 Les coefficients de la matrice
Mn
tendent vers 0,8 ou vers 0,2.
On en déduit
L
0,8 0,2
0,8 0,2 .=
 On note que les deux lignes de
L sont iden-
tiques.
 Calculons [0,8 0,2] 0,9 0,1
0,4 0,6 [ 0,72 0,08 0,08 0,12] ,×
=++
soit
M
[0,8 0,2] [ 0,8 0,2 ].×=
On donne
A =
010
05 0 05
010
,,,
B =
010
001
100
,
C =
00505
010
02 0 08
,,
,,
.
 a. Déterminer, à l’aide d’une calculatrice, les matrices
AB C
nnn
,, pour les
valeurs
n = 2, n = 3, n = 4.
Solution
Exercice
© Cned - Académie en ligne