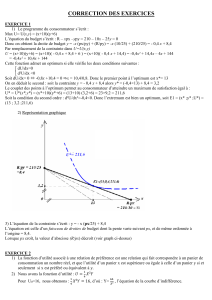
Microéonomie I: théorie du consommateur Analyse - Sen

Microéonomie I: théorie du consommateur
Analyse microéconomique du comportement du consommateur : préférences et contrainte
budgétaire par Simonet Jean-Paul
Sommaire
 Des préférences à l’utilité
 Les courbes d’indifférence
 Utilité marginale et taux de substitution
 La contrainte budgétaire
Il s’agit d’expliquer le comportement d’un individu disposant d’un revenu monétaire donné et
cherchant à satisfaire des besoins par l’acquisition de biens et services ayant un prix.
Notre consommateur a un objectif - satisfaire des besoins - et il est soumis à une contrainte - son
pouvoir d’achat qui dépend du revenu dont il dispose et des prix des produits.
Pour traiter ce problème il faut attribuer au consommateur et à son environnement certaines
caractéristiques.
Le consommateur doit être capable d’apprécier son état de satisfaction, il doit pouvoir dire s’il
préfère la situation A à la situation B et son jugement doit respecter des règles de cohérence : c’est
l’objet de la théorie de l’utilité.
L’environnement doit s’imposer au consommateur, il doit être contraignant ce qui revient à dire que
le consommateur sait parfaitement que "choisir c’est exclure", chaque décision ayant un coût
d’opportunité .
Des préférences à l’utilité
Les économistes savent parfaitement que les "préférences" du consommateur ne tombent pas du
ciel, et que les "goûts" individuels sont socialement construits donc susceptibles d’être influencés.
Pour essayer de construire une représentation du comportement du consommateur face aux
décisions qu’il doit prendre il faut cependant raisonner "toutes choses égales par ailleurs" ce qui
revient à traiter les préférences comme si elles étaient entièrement données (les économistes disent
qu’elles sont exogènes). Les développements de l’analyse permettent d’intégrer des phénomènes
d’interdépendance et d’améliorer le réalisme de la présentation.
Pour l’instant nous nous en tiendrons à la version "basique".
Un grand nombre de produits sont offerts aux choix du consommateur. Ce dernier constitue un
panier de consommation en choisissant des quantités de certains produits. Le consommateur est
supposé être capable de classer ses préférences c’est-à-dire d’indiquer s’il préfère consommer le
panier A ou le panier B.
La relation de préférence s’écrit
si le panier A est préféré ou équivalent au panier B,

Microéonomie I: théorie du consommateur
si A est strictement préféré à B et
si A est équivalent (indifférent) à B.
Cette relation permet de classer les paniers mais pour qu’elle soit une relation de préordre complet
au sens des mathématiciens (ce qui permet ensuite de lui associer une fonction d’utilité) il faut faire
trois hypothèses particulières : les axiomes des préférences [1].
Cette axiomatique des préférences fonde la rationalité du comportement du consommateur, qui de
ce fait est soumise à la même faiblesse logique : elle repose sur des hypothèses invérifiables [2].
Les trois axiomes sont : l’axiome de totalité, l’axiome de réflexivité et l’axiome de transitivité.
- L’axiome de totalité énonce que pour tous les paniers de consommation A et B le consommateur
est toujours capable de dire que
- La réflexivité signifie simplement qu’un panier est toujours au moins équivalent à lui même
- La transitivité implique que si le panier A est préféré ou indifférent au panier B et si le panier B est
préféré ou indifférent au panier C, alors le panier A est préféré ou indifférent au panier C.
Les trois propriétés précédentes suffisent à faire de cette relation de préférence ce que les
mathématiciens appellent une relation de préordre complet sur l’ensemble des paniers de
consommation envisagés par le consommateur.
Si la relation de préférence est une relation de préordre total, on peut lui associer une fonction
d’utilité U qui est une application de l’espace des produits dans celui des nombres réels. Cette
application associe aux quantités consommées x et y des marchandises (X et Y) des nombres U tels
que si le panier constitué d’une quantité x1 du bien X et y1 du bien Y est préféré à celui constitué des
quantité x2 du bien X et y2 du bien Y alors le nombre représentant l’utilité du premier panier est
supérieur à celui du second panier.
Les nombres associés aux paniers de consommation sont des indices d’utilité, situant un panier
relativement aux autres.

Microéonomie I: théorie du consommateur
Du point de vue de l’analyse économique la référence à l’utilité est introduite par Daniel Bernouilli
dans Théorie sur la mesure du risque (1738) [3]. Mais c’est Heinrich Gossen qui a proposé en 1854 [4]
la première version d’une théorie de l’utilité. Selon Herman Heinrich Gossen la consommation d’une
unité supplémentaire d’un bien augmente l’utilité totale ressenti par le consommateur, mais l’utilité
procurée par cette dernière unité consommée est plus faible que celles procurée par l’unité
précédente. Ainsi la fonction d’utilité liant quantité consommée et utilité procurée est une fonction
croissante mais de moins en moins vite : on dit que l’utilité marginale est décroissante.
Mathématiquement l’indice d’utilité associé à la quantité x consommée du bien X est telle que :
U = f(x)
U’x= dU / dx > 0
U"x= d2U / dx2 < 0
En supposant qu’un individu est capable d’attacher un indice d’utilité à la consommation d’un bien
revient à dire que l’utilité est mesurable, c’est une théorie de l’utilité cardinale . C’est cette
conception qui est retenue par les fondateurs de l’analyse marginaliste : Léon Walras, Carl Menger et
Stanley Jevons. Conscient de l’impossiblité de mesurer directement l’utilté Vilfredo Pareto introduit
la théorie de l’utilité ordinale . Dans la conception ordinale les indices doivent simplement respecter
l’ordre des préférences pas les "mesurer".
Le passage de la conception cardinale de l’utilité à la conception ordinale revient simplement à
admettre qu’il existe plusieurs fonctions d’utilité respectant les préférences du consommateur [5].
Admettons que les trois hypothèses permettant de passer de la relation de préférence à la fonction
d’utilité sont remplies (la relation de préférence est totale, réflexive et transitive).
Admettons en plus que les quantités consommées des biens et les préférences associées peuvent
varier de manière infinitésimale, c’est-à-dire continue.
On peut considérer comme vraisemblable le fait que toute augmentation de la consommation de l’un
des produits du panier, sans diminution de la consommation des autres, augmente l’utilité de ce
panier.
Il n’est pas absurde de penser que le plus souvent pour une même utilité procurée par un panier
composé d’un seul bien et un panier composé de plusieurs biens le consommateur choisira le
second, ce qui traduit une préférence pour les mélanges (ou pour la variété).
Ces trois hypothèses complémentaires [6] correspondent à trois propriétés mathématiques de la
fonction d’utilité, la continuité, la monotonicité et la convexité.
Sous ces hypothèses (cette axiomatique des préférences), la fonction d’utilité peut être représentée
graphiquement en respectant les propriétés exigées. Dans le cas simple [7] de paniers constitués de
deux biens X et Y on a par exemple le graphique suivant :

Microéonomie I: théorie du consommateur
Sur ce graphique les paniers A, B et C procurent la même utilité U*, autrement dit Ua = Ub = Uc = U*.
Pour le consommateur il est indifférent de consommer A, B ou C.
En revanche le panier D est préféré aux trois autres.
Cette représentation en trois dimensions est délicate, il est plus commode de s’en tenir à deux
dimensions par exemple en observant tous les paniers procurant une même utilité. Graphiquement
cela revient à couper l’axe vertical de la représentation en trois dimensions par un plan parallèle au
repère constitué par les axes des quantités de produits. En coupant la surface représentant la
fonction d’utilité par un plan pour un niveau d’utilité donné (par exemple U*) on obtient une "trace"
qui donne tous les paniers "indifférents" donnant une utilité U*.

Microéonomie I: théorie du consommateur
Les courbes d’indifférence
Pour un panier de deux biens une courbe
d’indifférence du consommateur est l’ensemble des paniers de ces deux biens qui ont la même utilité
pour le consommateur. Ici les quantités (x1, y1) et (x2, y2) des biens X et Y donnent la même utilité : le
consommateur est indifférent face au choix du panier A1 ou du panier A2. En mettant une quantité
plus grande de bien Y dans le panier A1 l’utilité de ce nouveau panier augmente. On peut obtenir la
même utilité que celle de ce nouveau panier B1 en modifiant le panier A2 par une augmentation de la
quantité du bien Y. Le panier B2 correspond à un indice d’utilité plus grand que celui du panier A2 et
identique à celui du panier B1.
Plus les courbes d’indifférence sont éloignées de l’origine des axes plus l’indice d’utilité auquel elle
corresponde est élevé. Cela revient à considérer que le consommateur est insatiable, ce qui peut
s’exprimer de manière "savante" - la propriété mathématique de monocité est aussi l’axiome de la
non saturation des préférences – ou de manière triviale – le consommateur « veut toujours plus ».
Si les préférences sont transitives les
courbes d’indifférence ne peuvent pas se couper. Un raisonnement par l’absurde permet de le
montrer facilement. Sur le graphique on voit que les paniers A1 et A2 sont indifférents et qu’il en va
de même pour A1 et B2. C’est impossible car le panier B2 a une plus grande utilité que le panier A2
puisqu’il contient la même quantité du bien X mais une plus grande quantité du bien Y.