Chapitre 2 MOUVEMENT DE TRANSLATION

Chapitre 2
MOUVEMENT DE TRANSLATION
MOUVEMENTS RECTILIGNES
Sommaire
–1. Mouvement rectiligne uniforme
–2. Mouvement rectiligne uniformément accéléré
–3. Mouvement rectiligne uniformément décéléré
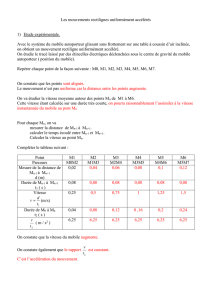
1. MOUVEMENT RECTILIGNE UNIFORME
Un piéton se promène dans un parc. L'allée qu'il suit est en ligne droite. Sa trajectoire
est donc rectiligne. .
Examinons maintenant son mouvement.
Nous remarquons que ce piéton met constamment 60 s pour parcourir chaque espace de
100 m. Si nous divisons son trajet en espaces de 50 m, nous constatons qu'il met
systématiquement 30 s pour parcourir chaque espace de 50 m. Partageons maintenant
son parcours en espace de 25 m et constatons qu'il met 15 s pour parcourir chaque
espace de 25 m.
Nous en déduisons que le piéton parcourt des espaces égaux en des temps égaux :
–60 s pour chaque espace de 100 m;
–30 s pour chaque espace de 50 m;
–15 s pour chaque espace de 25 m.
Son mouvement est régulier. On dit qu'il est uniforme. Étant donné que sa trajectoire
est rectiligne, nous pouvons dire que son mouvement est rectiligne uniforme.
1.1 Définition
Le mouvement d'un mobile est rectiligne uniforme s'il parcourt, sur une droite et
toujours dans le même sens, des espaces égaux en des temps égaux, quels que soient ces
temps.
Théorie chapitre 2 – page 1

1.2 Lois du mouvement
L'exemple nous fait remarquer que, pour parcourir 100 m, le temps est de 60 s et, pour
parcourir 25 m, le temps est de 15 s.
Cela veut dire que si l'espace parcouru est 4 fois plus petit, le temps mis pour le
parcourir est également 4 fois plus petit.
Si nous faisons la comparaison dans le sens inverse, nous constatons que pour parcourir
25 m, le temps est de 15 s et, pour parcourir 50 m, le temps est de 30 s. Par conséquent,
si l'espace parcouru est 2 fois plus grand, le temps mis pour le parcourir est également 2
fois plus grand.
Loi des espaces : dans tout mouvement rectiligne uniforme, l'espace parcouru est
proportionnel au temps mis à le parcourir.
Il nous reste à découvrir ce facteur de proportionnalité.
Que peut-on dire du piéton qui parcourt des espaces égaux en des temps égaux ? C'est
qu'il marche toujours à la même vitesse. En effet, il ne marche jamais plus vite ni moins
vite. Sa vitesse est constante.
Loi des vitesses : dans tout mouvement rectiligne uniforme, le quotient de l'espace
parcouru par le temps mis à le parcourir est constant : c'est la vitesse.
Nous pouvons éventuellement, à la lumière de ces lois, définir le mouvement rectiligne
uniforme comme étant le mouvement d'un mobile dont la trajectoire est rectiligne et la
vitesse constante.
1.3 Formules
Désignons chaque élément :
En vertu des lois du mouvement et en particulier la loi des vitesses, nous pouvons
établir :
Cette formule peut prendre les formes suivantes :
e = v * t t = e / v
Théorie chapitre 2 – page 2
Vitesse v m/s
Espace e m
Temps t s

1.4 Représentation graphique
Il est important de savoir ce que nous permet un graphique. Un graphique permet d'avoir
directement une vue d'ensemble de l'évolution d'un phénomène.
Prenons par exemple les graphiques de température et de rythme cardiaque utilisés par
les médecins dans les hôpitaux.
Il est donc intéressant d'utiliser la méthode graphique pour représenter le déplacement
d'un mobile animé d'un mouvement rectiligne uniforme.
Prenons un exemple pratique pour nous permettre d'élaborer les graphiques du
mouvement :
Un cyclomoteur roule à la vitesse constante de 12 m/s pendant 20 s. Quel espace a-t-il
parcouru pendant ce temps ?
Donnée(s) Inconnue(s) Formule(s) Solution
v= 120 m/s
t= 20 s
e = ? m v = e / t
e = v * t
e = 12 * 20 = 240 m
1.5 Diagramme des espaces
Le diagramme des espaces va représenter l'évolution de l'espace parcouru en fonction
du temps.
Le graphique va présenter deux axes perpendiculaires, dont :
–l'axe horizontal (Ot) sera l'axe des temps (en s);
–l'axe vertical (Oe) sera l'axe des espaces (en m);
–l'intersection (O) sera l'origine des axes.
Voyons l'évolution de l'espace parcouru seconde après seconde :
à l'instant l'espace parcouru est de :
t = 0 s e = v * t = 12 * 0 = 0 m
t = 1 s e = v * t = 12 * 1 = 12 m
t = 2 s e = v * t = 12 * 2 = 24 m
t = 3 s e = v * t = 12 * 3 = 36 m
t = 4 s e = v * t = 12 * 4 = 48 m
t = 5 s e = v * t = 12 * 5 = 60 m
Théorie chapitre 2 – page 3

t = 6 s e = v * t = 12 * 6 = 72 m
t = 7 s e = v * t = 12 * 7 = 84 m
t = 8 s e = v * t = 12 * 8 = 96 m
t = 9 s e = v * t = 12 * 9 = 108 m
t = 10 s e = v * t = 12 * 10 = 120 m
t = 11 s e = v * t = 12 * 11 = 132 m
t = 12 s e = v * t = 12 * 12 = 144 m
t = 13 s e = v * t = 12 * 13 = 156 m
t = 14 s e = v * t = 12 * 14 = 168 m
t = 15 s e = v * t = 12 * 15 = 180 m
t = 16 s e = v * t = 12 * 16 = 192 m
t = 17 s e = v * t = 12 * 17 = 204 m
t = 18 s e = v * t = 12 * 18 = 216 m
t = 19 s e = v * t = 12 * 19 = 228 m
t = 20 s e = v * t = 12 * 20 = 240 m
Théorie chapitre 2 – page 4

Reportons maintenant sur le graphique suivant tous les éléments obtenus par le calcul.
Que constatons-nous en joignant les différents points obtenus par calcul ?
Le diagramme du mouvement rectiligne uniforme est une droite oblique par rapport aux
deux axes et dont l'origine est l'origine des axes.
Ce diagramme va nous permettre, par lecture directe, de trouver rapidement la solution
de problèmes simples : déterminer l'espace parcouru après un certain temps ou encore
rechercher le temps mis pour parcourir un certain espace.
Théorie chapitre 2 – page 5
t (s)
e (m)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
0
20
40
60
80
100
120
140
160
180
200
220
240