Exercice 1 Exercice 2 F r P r T r P r V v V v V varar Plot

TS1 - Correction du DS n°3
Exercice 1
1. P = mg =1030×9,8 = 10094 N, soit 1,01 kN
2. a) La vitesse de l’automobile passe de 0 à 100 km.h–1,
soit 100/3,6=27,8 m.s–1 en 11,1 s, son accélération
moyenne est donnée par : 5,2
1,11 8,27 == Δ
Δ
=t
v
am.s–2.
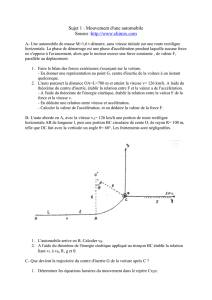
b) On applique la 2ème loi de Newton au système
{automobile}, en mouvement dans le référentiel terrestre
considéré comme galiléen.
Le système est soumis aux forces représentées ci-dessous
au point G :
La 2ème loi de Newton s’écrit : P
r+NR
r+mF
r
= Gam r
⋅.
Le mouvement est rectiligne horizontal donc les forces NR
r
et P
rse compensent, soit mF
r
=am
r
⋅
. En projection sur un
axe horizontal orienté de la gauche vers la droite, cela
donne : Fm=ma, soit Fm = (1030 + 70)×2,5 = 2750 N.
c) Avec 3 passagers supplémentaires, l’accélération
devient : a’ = Fm / Mtotale = 2750 / 1310 = 2,1 m.s–2.
Par définition, dt
dv
a= donc v(t) est une primitive de l’accélération.
Soit v(t) = a’⋅t + Cte. Or à t=0, l’automobile démarre sans
vitesse initiale, donc Cte = 0.
D’où v(t) = a’⋅ t = 2,1 t.
La vitesse v = 100 km.h–1, soit 27,8 m.s–1 est atteinte
lorsque s
a
v
t213
12 827 ,
,, '=== . L’indication est incomplète.
3. a) Puisque la résultante de forces se ramène à mF
r
constante, la masse étant constante, la 2ème loi de Newton
montre que l’accélération est également constante.
b) v(t) est une primitive de l’accélération a0 telle que à t=0
on ait v = 0. Donc v(t) = a0⋅t.
c) Comme, par définition, dt
dx
v=, 2
0
2
1
)( tatx ⋅= , sachant
qu’à t=0, l’automobile est située en O, origine du repère.
d) Pour t = 17,6 s, l’automobile a parcouru x = 400 m,
donc 2
2
058,2
6,174002 −
⋅=
×
=sma d’où NamFm2841=⋅= .
e) L’automobile a parcouru 400 m au bout de 17,6 s, donc
v(17,6) = 2,58×17,6 = 45,4 m.s–1 = 163 km.h–1.
Exercice 2
1. Le système étudié est un mobile sur coussin d’air se
déplaçant par-rapport au référentiel terrestre, considéré
comme galiléen.
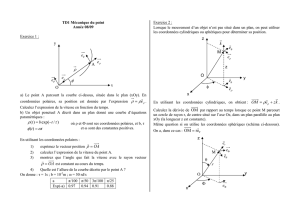
2. Schéma du dispositif :
3. 1
25,0
80
40 −
⋅== smv ; v4 = 0,53 m.s–1 et v6 = 0,59 m.s–1.
5. 2
3
333
1080 260 −
−⋅=
⋅
=sma ,
, ; a5 = 2,8 m.s–2.
6. Voir cours
8. La force de tension du ressort n’était pas constante
puisque l’accélération variait.
mF
r
G
NR
r
P
r
Plot fixe
Mobile sur
coussin d’air
G
T
r
NR
r
P
r
Echelles
y 1cm représente 2 cm en réalité
y vitesses : 1cm ↔ 0,2 m.s–1
y accélérations : 1 cm ↔ 1 m.s–2
2V
v
4V
v
6V
v
3a
r
5a
r
Plot