FICHE N. 1 : MÉCANIQUE ET GRAVITÉ Exercice 1 : rappels de

Licence de Sciences de la Terre – S3 – Physique Année 2016-2017
FICHE N. 1 : MÉCANIQUE ET GRAVITÉ
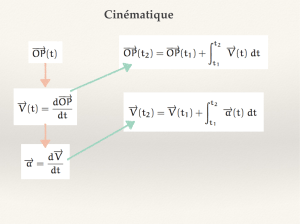
Exercice 1 : rappels de cinématique
La trajectoire d'un boulet de canon est donnée par le vecteur position suivant
1. Quelle est la position initiale du boulet ?
2. A quel(s) moment(s) touche-t-il le sol (z = 0) ? A quelle(s) position(s) ?
3. Tracer une représentation approximative de la trajectoire de ce boulet.
4. Calculer les coordonnées du vecteur vitesse
⃗ v ( M )
.
5. Que vaut la vitesse à l'instant
t=0
? Que représentent
v0
et
α
?
6. Que vaut l'accélération de M ? A quoi est-elle due ?
Exercice 2 : principe du gravimètre
On considère un ressort de raideur k placé horizontalement et attaché à une extrémité fixe. Lorsque l'autre extrémité
du ressort est en O, le ressort est au repos. Un bloc de masse m est posé sur le sol et attaché au ressort. Il glisse
sans frottement sur le sol. A l'instant
t=0
, il est éloigné de sa position d'équilibre d'une distance
x0
et lâché sans
vitesse initiale. On prendra l'axe
(Ox)
horizontal et l'axe
(Oz)
vertical.
1. Faire un bilan des forces appliquées au bloc. Donner leurs expressions dans la base de travail
(O ; ⃗ ux, ⃗ uy, ⃗ uz)
.
2. Appliquer le principe fondamental de la dynamique et établir l'équation différentielle du mouvement.
3. Montrer que
x=Acos (ωt+ϕ)
est une solution de cette équation. Donner l'expression de
ω
.
4. Quelles sont les valeurs minimales et maximales de x,
xmin
et
xmax
? Combien de temps mets le bloc pour
Sébastien Merkel – Pierre Hirel – Université Lille 1Page 1/4
⃗
OM =
{
x=x0+v0tcos (α)
y=y0
z=v0tsin (α)−1
2g t2
Le pendule simple
Ressort horizontal

Année 2015-2016 Licence de Sciences de la Terre – S3 – Physique
aller de
xmin
à
xmax
?
5. Comment mesurer la raideur du ressort à l'aide de ce dispositif ?
6. On considère maintenant un pendule, soit un fil de longueur l, auquel est attaché une masse m. L'angle
θ
mesure l'angle entre le fil et la verticale. Il dépend du temps. Dans ce cas, le principe fondamental de la
dynamique appliqué à la masse m permet de se ramener à l'équation différentielle du mouvement suivante :
Déterminer la solution de cette équation et la valeur de pulsation correspondante.
7. Comment utiliser ce dispositif comme gravimètre ? Un gravimètre permet de mesurer l'accélération de la
pesanteur
g
.
Exercice 3 : théorème de Gauss et champ de gravité de la Terre
On considère que la Terre est constituée de deux couches homogènes, le
noyau et le manteau. Le noyau a pour rayon
RN=3480
km et a pour masse
volumique moyenne
ρN=10900
kg.m-3. Le manteau à pour rayon
RM=6370
km et a pour masse volumique moyenne
ρM=4460
kg.m-3.
On rappelle la valeur numérique de la constante de gravitation universelle
G=6,67.10−11
SI.
1. Calculer le volume et la masse du noyau.
2. Calculer le volume et la masse du manteau.
3. On s'intéresse au champ de gravité à l'intérieur du noyau. Donner
l'expression de ce champ
g(r)
où
r
est la distance au centre de la
terre. Calculer la valeur numérique de
g(r)
au centre de la terre et à
la surface de noyau.
4. On s'intéresse au champ de gravité à l'intérieur du manteau. Donner l'expression de ce champ
g(r)
où
r
est la distance au centre de la terre. Calculer la valeur numérique de
g(r)
à la surface du manteau (de la
terre).
5. On s'intéresse au champ de gravité à l'extérieur de la terre. Donner l'expression de ce champ
g(r)
où
r
est la distance au centre de la terre. Calculer la valeur numérique de
g(r)
à 10000 km du centre de la
terre.
6. Tracer la courbe du champ de gravité exercé par la terre dans le cadre d'un tel modèle en utilisant les
résultats des questions 4, 5, et 6.
Exercice 4 : effets de forme et de rotation sur le champ de gravité
On cherche maintenant à évaluer les effets de la forme et de la rotation de la Terre sur le champ de gravité mesuré
en surface.
On supposera que la Terre a la forme de l'ellipsoïde de référence, avec un rayon de a = 6378 km à l'équateur et
b = 6357 km aux pôles. A la latitude de Paris (49° de latitude nord), la surface de l'ellipsoïde se trouve à 6366 km
du centre de la Terre.
Page 2/4 Sébastien Merkel – Pierre Hirel – Université Lille 1
ld2θ
dt2+gθ=0
Un modèle de Terre à deux
couches

Licence de Sciences de la Terre – S3 – Physique Année 2016-2017
On rappelle la valeur numérique de la constante de
gravitation universelle
G=6,67.10−11
SI, de la masse de
la Terre MT = 5,97.1024 kg, ainsi que l'expression de la
force centrifuge
Cette force peut aussi s'écrire comme
⃗
Fc=m ⃗ ac
où
⃗ ac
est l'accélération due à la force centrifuge.
1. Déterminer l'expression de
ω
, la vitesse de
rotation angulaire de la Terre autour de son axe.
Calculer sa valeur numérique.
2. Calculer les normes de l'accélération due à la force
centrifuge à l'équateur, à Paris, et au pôle nord. On
donnera les résultats avec 3 chiffres après la virgule. Représenter l'ellipsoïde de référence et ces 3
accélérations centrifuges sur un schéma.
3. Estimer la norme du champ de gravité
⃗ g
exercé par la terre à l'équateur, à Paris, et au pôle nord. On
donnera les résultats avec 3 chiffres après la virgule. Représenter l'ellipsoïde de référence et ces 3 champs
de gravité sur un schéma.
4. Il est fréquent d'ajouter le champ de gravité et la composante normale (perpendiculaire à la surface de la
Terre) de la force centrifuge pour estimer le champ de gravité effectif à la surface du globe. Pourquoi ?
Donner l'expression de la norme de
⃗ geff
en fonction des normes de
⃗ ac
et
⃗ g
et de
Φ
(la latitude).
5. Calculer la valeur de la norme de
⃗ geff
à l'équateur, à Paris, et au pôle nord. On donnera les résultats avec 3
chiffres après la virgule.
6. Les mesures réelles sont les suivantes : pôle Nord, 9,832 m.s-2 ; Paris, 9,809 m.s-2 ; équateur, 9,7803 m.s-2.
Commenter ces mesures au regard des résultats de la question précédente.
Exercice 5 : bases de la gravimétrie
On considère une grotte de forme sphérique de rayon
R=90
m. Le centre
C
est à
P=100
m sous la surface, à
la verticale de l'origine du repère de travail
O
. Pour la croûte autour de la grotte,
ρ≈3000
kg.m-3. On rappelle
aussi la valeur numérique de la constante de gravitation universelle
G=6,67.10−11
SI.
On cherche à analyser la perturbation du champ de gravité en surface due à la grotte. On écrit donc
⃗ g= ⃗ gT+δ ⃗ g
,
où
⃗ g
est le champs mesuré en surface,
⃗ gT
le champ de gravité terrestre (non perturbé), et
δ ⃗ g
la perturbation due
à la grotte.
Sébastien Merkel – Pierre Hirel – Université Lille 1Page 3/4
⃗
Fc=m r ω2 ⃗ ur

Année 2015-2016 Licence de Sciences de la Terre – S3 – Physique
1. Établir l'expression de
d=OM
en fonction de
P
et
Φ
. Calculer sa valeur numérique pour
Φ=0°
,
30°, 60°, et 80°.
2. Établir l'expression de
r=CM
en fonction de
P
et
Φ
.
3. Établir l'expression de
δ ⃗ g
en fonction des données du problème et montrer qu'elle peut se mettre sous la
forme
δ ⃗ g=−Ccos2Φ ⃗ ur
où
C
est une constante dont la valeur numérique est 6,12.10-5 m.s-2. Donner
l'expression littérale de
C
en fonction des données du problème.
4. Remplir le tableau suivant. Le mgal est une unité très utilisée en gravimétrie. On a 1 mgal = 10-5 m.s-2.
Φ
d
(m)
∥δ ⃗ g∥
(m.s-2)
∥δ ⃗ g∥
(mgal)
0°
30°
60°
80°
Pourquoi travaille-t-on en mgal ?
5. Représenter la variation de
∥δ ⃗ g∥
en fonction de
d
. On fera varier
d
de –600 à +600 m.
6. Imaginez un système permettant la détection de grottes à l'aide de mesures en surface.
Exercice 6 : géoïde
On cherche maintenant à étudier l'influence d'une structure souterraine sur le géoïde. Pour simplifier les calculs, on
considère une surface terrestre plane et une structure sphérique, de rayon
R=20
km, et dont le centre se trouve à
une profondeur
P=25
km.
Dans un premier temps, la structure est plus dense que la croute environnante et
Δ ρ≈100
kg.m-3. Les calculs de
l'exercice 5 donnent les résultats suivants
Φ
d
(km)
∥δ ⃗ g∥
(mgal)
0° 0 35,8
30° 14,4 26,8
45° 25,0 17,9
60° 43,3 8,9
80° 141,8 1,1
1. Représenter le vecteur
δ ⃗ g
en surface en fonction de
d
. On fera varier
d
entre -50 et +50 km. On pourra
se limiter à une représentation approximative. Les paramètres importants sont la longueur des vecteurs et
leurs orientations. Comment trouvez-vous l'orientation de
δ ⃗ g
?
2. Représenter les vecteurs
⃗ g
du champ de gravité total en surface en fonction de
d
. On pourra amplifier les
effets de
δ ⃗ g
.
3. Tracer la position approximative du géoïde en fonction de
d
.
4. Une source d'eau émerge à
d=−5
km. Où s'écoule-t-elle ?
5. On considère maintenant une structure est moins dense que la croute environnante, avec toujours
Δ ρ≈100
kg.m-3. Les valeurs du tableau restent les mêmes. Reprendre les questions 1 à 3.
Page 4/4 Sébastien Merkel – Pierre Hirel – Université Lille 1