5 La chaleur

Chaleur
13
La chaleur
5 La chaleur
5.1 Le contact thermique des corps
Lorsqu’on met en contact thermique deux corps de températures différentes, ils nissent par
atteindre une température commune quelconque située entre les deux températures initiales. On
dit que de la chaleur est passée du corps 1e plus chaud vers le corps le plus froid. Tout comme la
force ou la lumière, la chaleur fait directement appel à nos sens et nous en avons tous une notion
intuitive. Pourtant, sa signication comporte une subtilité qui n’a été éclaircie qu’au bout de
plusieurs décennies. Jusqu’au milieu du XVIIIe siècle, les termes chaleur et température avaient
une signication pratiquement identique. Par exemple, on graduait les thermomètres en «degrés de
chaleur». En 1760, Joseph Black fut le premier à établir distinction nette entre la température, que
mesure un thermomètre, et la chaleur, équilibre les températures d’un corps chaud et d’un corps
froid en s’écoulant de l’un à l’autre.
La théorie du uide calorique ne permettait pas d’expliquer la production de chaleur par frottement
qui survient par exemple lorsque nous nous frottons les mains pour les réchauffer. Le scientique
américain Benjamin Thompson, qui devint plus tard le Comte Rumford de Bavière avait des doutes
quant à la nature matérielle du uide calorique, qui ne paraissait pas avoir de masse.
En 1798, alors qu’il surveillait les opérations d’alésage des canons, il fut frappé par la chaleur
considérable qui était produite. Il fallait constamment renouveler l’eau qui servait à refroidir le
métal, car elle s’évaporait en bouillant. Selon la théorie du uide calorique, les petits copeaux de
métal découpés dans le canon ne pouvaient garder leur uide calorique et le libéraient dans l’eau.
Rumford t une observation qui mettait en doute cette explication même lorsque l’outil était devenu
si émoussé qu’il ne parvenait plus à couper le métal, l’eau continuait à se réchauffer. De plus, il
montra les copeaux de métal n’avaient aucunement perdu leur «capacité à emmagasiner le uide
calorique». Il semblait donc évident que la source de chaleur produite par le frottement lors de ces
expériences était inépuisable et ne pouvait être une substance matérielle.
Nous avons fortement tendance à concevoir la chaleur comme emmagasinée dans un système.
L’impression intuitive qu’un corps possède quelque chose de plus lorsqu’il est chaud que lorsqu’il
est froid est bien correcte, mais nous allons voir qu’il s’agit d’énergie interne, et non de chaleur. La
relation entre chaleur et énergie interne fait l’objet du Premier principe de la thermodynamique.
5.2 La chaleur spécique
Joseph Black fut le premier à se rendre compte que l’élévation de température d’un corps pouvait
servir à déterminer la quantité de chaleur absorbée par ce corps. Si une quantité de chaleur Q produit
une variation de température ∆T dans un corps, sa capacité thermique est dénie par
capacité thermique =
Q
TD
L’unité SI de capacité thermique est le J/K. On utilise parfois une unité (non SI) de chaleur, la calorie,
qui était autrefois dénie comme la quantité de chaleur nécessaire pour élever la température de 1 g
d’eau de 14,5°C à 15,5°C. À l’heure actuelle, la calorie est dénie en fonction du joule : 1 calorie
= 4,186 J. La quantité de chaleur Q nécessaire pour produire une variation de température ∆T est
proportionnelle à la masse de l’échantillon m et à ∆T (pour les petites valeurs de ∆T). Elle dépend
également de la substance considérée. L’équation suivante combine toute ses relations :
Q mc T= D

Chaleur
14
La chaleur
Où c est la chaleur spécique du matériau. On peut utiliser l’équation précédente pour déterminer
la chaleur transmise à un corps ou par un corps. En exprimant la forme:
cm
Q
T
=1
D
on voit que la chaleur spécique est égale à la capacité thermique par unité de masse. Son unité SI
est le J/kgK. La chaleur spécique est une propriété caractéristique d’une substance donnée, alors
que la capacité thermique correspond à un échantillon donné de la substance. On voit dans les tables
que la chaleur spécique de l’eau est grande par rapport aux valeurs des autres substances.
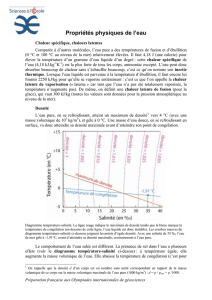
La chaleur spécique d’une substance varie en général avec la température. Dans le cas de l’eau,
elle varie de quelques pour cent entre 0°C et 100°C. La chaleur spécique varie brutalement lorsque
la substance passe de l’état solide à l’état liquide ou de l’état liquide à l’état gazeux. Elle dépend
également des conditions dans lesquelles la chaleur est fournie à la substance. Par exemple, la
chaleur spécique cp d’un gaz maintenu à pression constante est différente de sa chaleur spécique
cv à volume constant.
Pour l’air,
c J kg K
v= ×708
et
c J kg K
p= ×1000
. Pour les solides et les liquides, la différence est
en général petite et dans la pratique on mesure habituellement cp.
La méthode des mélanges
Mise au point par Black, la méthode des mélanges consiste à déterminer la chaleur spécique
d’un corps en le plaçant en contact thermique avec un autre corps dont on connaît la chaleur
spécique. Supposons que l’objet dont on doit déterminer la chaleur spécique ait une masse m1
et soit à une température initiale T1. Un liquide de masse m2, à la température initiale T2, se trouve
dans un récipient à l’intérieur d’une enceinte isolée thermiquement, que l’on nomme calorimètre.
On plonge l’objet dans le liquide et on relève la température d’équilibre nale Tf. Puisqu’il n’y a
pas d’échange de chaleur avec le milieu ambiant, la chaleur transmise au corps froid est égale à la
chaleur perdue par le corps chaud:
Q Q
1 2 0+ =
L’hypothèse de Black reposait sur la notion de «conservation du uide calorique». Il fut capable de la
justier par la cohérence des valeurs obtenues pour les chaleurs spéciques de diverses substances.
On se rend compte maintenant que l’équation précédente est un cas particulier de la conservation de
l’énergie. En fonction des masses et des chaleurs spéciques des deux corps, l’équation devient
m c T m c T
1 1 1 2 2 2 0D D+ =
où
DT T T
f1 1
= -
et
DT T T
f2 2
= -
Ces variations de températures sont de signes opposés. On se sert de calorimètres pour mesurer
les chaleurs de combustion des réactions chimiques. C’est ainsi que l’on détermine les «valeurs
énergétiques» des aliments et des combustibles. Dans la pratique, des corrections doivent être
apportées pour tenir compte de la capacité thermique du récipient du calorimètre
Exemple
Un bloc de cuivrre de 1 kg à 80°C est plongé dans 1 kg d’eau à 20°C. Calculer la température
d’équilibre des deux corps.
5.3 La chaleur latente
Black s’aperçut que l’apport de chaleur à un système ne faisait pas toujours varier sa température.

Chaleur
15
La chaleur
La température reste en effet constante lorsqu’une substance
change de phase, lorsqu’elle passe par exemple de l’état
solide à l’état liquide ou de l’état liquide à l’état gazeux. Il t
remarquer que, si la quantité de chaleur nécessaire pour faire
fondre la glace était faible, le dégel brutal qui en résulterait au
printemps provoquerait des inondations catastrophiques.
Soit un échantillon de glace à une température initiale
arbitraire, -10°C par exemple. Si on lui fournit de la chaleur
progressivement, sa température va tout d’abord s’élever.
Mais lorsque sa température atteint 0°C, la glace commence
à fondre et reste à 0°C jusqu’à ce qu’elle soit complètement
transformée en liquide. L’absorption de la chaleur ne se
traduit pas par une élévation de température. Les mesures effectuées montrent qu’il faut environ
330 kJ pour transformer en liquide 1 kg de glace à 0°C. Black donna à cette chaleur «dissimulée»
le nom de chaleur latente de fusion, Lf. Une fois que toute la glace a fondu, la température
s’élève régulièrement jusqu’à 100°C. À ce stade, le liquide commence à se transformer en gaz et
la température demeure à nouveau constante. Lorsque toute l’eau est passée à l’état de vapeur, la
température recommence à s’élever. À une pression de 1 atm (
1 013 105 ,×Pa
), la chaleur latente de
vaporisation Lv de l’eau est égale à
23 105 ×J kg
. À d’autres pressions, la température à laquelle
les phases liquides et gazeuse sont en équilibre est différente et la valeur de la chaleur latente l’est
également.
Considérons un échantillon de masse m qui change de phase. La chaleur qu’il échange avec
son milieu ambiant est liée à la chaleur latente L par la relation:
Q mL=
La chaleur latente est « dissimulée » en ce sens qu’il n’y a pas de variation de température; toutefois,
l’énergie n’est pas perdue. Lorsque l’eau se condense de la phase gazeuse en phase liquide, chaque
kilogramme libère la chaleur latente de vaporisation. De même, lorsque le liquide se convertit en
phase solide, chaque kilogramme libère la chaleur latente de fusion.
En général, une phase donnée d’une substance est caractérisée par un certain arrangement
des molécules. Physiquement, la chaleur latente de fusion représente le travail nécessaire pour
rompre les liaisons entre les molécules dans la phase solide et pour leur permettre de se déplacer
facilement les unes par rapport aux autres dans la phase liquide. La chaleur latente de vaporisation
est nécessaire pour accroître la distance entre les molécules au passage de la phase liquide à la phase
gazeuse. D’autres types de changement de phase correspondent, par exemple, à des modications
de la structure cristalline ou de l’aimantation.
I1 faut souligner que la chaleur latente de vaporisation est nécessaire pour un changement de phase,
même si la température du liquide est bien inférieure à son point normal d’ébullition. Ainsi, lorsque
l’eau s’évapore à la température ambiante, la quantité de chaleur appropriée doit être fournie par
le milieu ambiant. C’est pourquoi l’eau a tendance à refroidir une surface, la peau par exemple,
lorsqu’elle s’en évapore. La valeur de Lv est légèrement plus élevée lorsque la température est
inférieure au point d’ébullition. La valeur de la chaleur latente dépend également de la pression à
laquelle a lieu le changement de phase.
Exemples
1. On plonge un bloc de glace de 2 kg à - 10°C dans 5 kg d’eau liquide à 45°C. Quelle est la
température nale du système?

Chaleur
16
La chaleur
2. idem avec de l’eau à 20°C
Indication: Trois états nals sont possibles: le système est entièrement constitué de glace, d’un
mélange de glace et d’eau à 0°C ou entièrement constitué d’eau. Avant d’écrire une équation, il faut
déterminer l’état nal en tenant compte de la chaleur nécessaire à ces diverses transformations.
5.4 Exercices
5.1 Lorsqu’on fournit 400 J de chaleur à 150 g de liquide, sa température s’élève de 2,5 K. Quelle
est sa chaleur spécique?
5.2 On place une bille d’acier de 80 g à 180°C dans un calorimètre en cuivre de 90 g contenant
500 g d’eau à 15°C. Quelle est la température nale?
5.3 Une bille en plomb de 250 g à 210°C est placée dans un calorimètre en aluminium de 90 g qui
contient 300 g de liquide à 20°C. Si la température nale est de 30°C, quelle est la chaleur
massique du liquide?
5.4 Une bouilloire électrique en acier de 0,5 kg et de puissance nominale 1200 W contient 0,6 kg
d’eau à 10°C. Combien de temps met l’eau pour atteindre 90°C? On suppose qu’il n’y a pas de
pertes.
5.5 En faisant un exercice léger, une personne produit de la chaleur à raison de 2 500 kJ/h. Si 60%
de cette chaleur est perdue par évaporation de l’eau, évaluez la masse d’eau perdue en 2 h. La
chaleur latente de vaporisation est égale à
23 105 ×J kg
.
5.6 Quelle est la quantité de chaleur nécessaire pour convertir 80 g de glace initialement à
- °10 C
en 60 g d’eau et 20 g de vapeur à 100°C ?
5.7 Un calorimètre en cuivre de 70 g contient 100 g d’eau. On ajoute dans l’eau 200 g de grenaille
de plomb à 200°C. (a) Quelle doit être la température initiale de l’eau pour que la température
nale soit égale à la température ambiante, 20°C ? (b) A quoi peut servir ce résultat ?
5.8 Une centrale nucléaire perd 500 MW de chaleur dans l’eau pompée d’un lac puis évacuée. Si la
température s’élève de 10°C, quel est le débit en kilogrammes par seconde ?
5.9 Le rayonnement solaire fournit une intensité d’environ 1 kW/m2 à la surface de la Terre. On
utilise un collecteur solaire de 3 m sur 2 m pour chauffer de l’eau. Quel doit être le débit de
l’eau, en kilogrammes par seconde, pour que l’élévation de température soit de 40°C. On
suppose que 80% de l’énergie solaire est absorbée par l’eau.
5.10 Le rayonnement solaire fournit une intensité d’environ 1 kW/m2 à la surface de la Terre. La
température de la glace d’un lac gelé est de –10°C. Calculer l’épaisseur de glace qui va fondre
en une journée de 6 h d’ensoleillement.
5.11 Un bécher troué contient de la glace à 0°C. De l’eau à même température s’écoule par le trou
du bécher à raison de 1 cm3/s. Calculer la puissance du système de chauffage.