1 Biens compléments parfaits.

Universit´ e Franc¸ois Rabelais - L1 AES
Cours d’Economie G´ en´ erale
Corrig´ e succinct du TD n◦6
Automne 2012
1 Biens compl´ ements parfaits.
Un agent obstin´ e choisit de ne consommer whisky (bien 2) et coca (bien 1) que dans les
proportions suivantes : x2= 2x1(et ceci ind´ ependemment du prix du whisky et du coca).
1) Dans cet exemple, le ratio entre les quantit´ es de bien 1 et de bien 2 optimalement
consomm´ ees est toujours identique et ´ egal ` a 2, et ceci, quels que soient les prix. Dans
d’autres cadres, ` a quoi s’attend-t’on concernant le rapport x∗
2/x∗ 1quand le prix relatif du
bien 1 augmente ?
La d´ enomination “compl´ ements parfaits” s’applique ` a cette r´ ealit´ e qui fait que la consom-
mation de deux biens se fait toujours dans les mˆ emes proportions. L’exemple le plus courant
est celui du caf´ e et du sucre. C’est un exemple qui semble naturel.
En fait, en ´ economie, il en va diff´ eremment pour la plupart des biens. En effet, la th´ eorie de
la consommation que l’on vient de d´ evelopper dans ce chapitre est que la consommation de
chacun des biens d´ epend de beaucoup de choses, des pr´ ef´ erences, des effets de modes, de
la n´ ecessit´ e, mais ... aussi, du prix de ces biens, et plus particuli` erement du PRIX RELATIF
de ces biens.
Si l’on reprend l’exemple du sucre et du caf´ e qui paraˆ ıt solide : deux biens compl´ ementaires.
Imaginez que pour une raison ou une autre, le prix du sucre soit tout d’un coup multipli´ e par
100, avec la cons´ equence qu’un caf´ e sucr´ e coˆ uterait deux fois plus qu’un caf´ e non sucr´ e.
Ne pensez-vous que certains adeptes du caf´ e sucr´ e passeraient au caf´ e sans sucre ?
La raison pour laquelle la proportion de consommation de deux biens peut diff´ erer suivant
les niveaux de prix et de revenu provient de cette propri´ et´ e que poss` ede le panier de consom-
mation optimale qui est l’´ egalit´ e du TMS de bien 1 en bien 2 avec le prix relatif du bien 1 en
bien 2. Si les prix du bien 1 vient ` a augmenter, le consommateur aura tendance ` a se mettre
dans une situation o` u son TMS de bien 1 est plus ´ elev´ e, cad quand la quantit´ e de bien 1 est
plus faible.
2) Quelle TMS de coca en whisky pourrait repr´ esenter les pr´ ef´ erences de ce m´ enage ?
Dans le cas consid´ er´ e, un consommateur qui a plus de deux fois de whisky que de coca est
dispos´ e` a c´ eder du whisky (bien 2) pour acqu´ erir du coca (bien 1). A quel taux ?
1

2 Comment pr´ evoir le changement de la demande d’un consom-
mateur ?
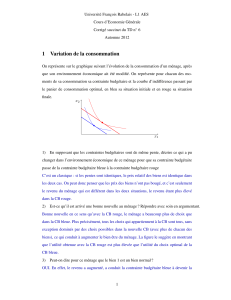
Soit un consommateur, Linh, initialement soumis ` a la contrainte budg´ etaire bleue. On
repr´ esente son choix optimal et la courbe d’indiff´ erence passant par ce choix optimal. On
ne connaˆ ıt rien d’autre de ses pr´ ef´ erences que cette courbe d’indiff´ erence trac´ ee dans le
graphique ci-apr` es.
x1
x2
Consid´ erez maintenant la contrainte budg´ etaire rouge correspondant ` a d’autres conditions
de revenu et de prix auxquels Linh est soumis [le prix relatif du bien 1 ↓]
1) Le bien-ˆ etre de Linh augmente-t’il ou non lorsqu’il est soumis ` a la CB rouge ?
La r´ eponse est non ambig¨ ue. Le bien-ˆ etre de Linh augmente, mˆ eme s’il ne peut plus b´ en´ eficier
du panier optimal qu’il avait choisi avec la contrainte budg´ etaire bleue. En effet, on re-
marque que la courbe d’indiff´ erence la plus ´ elev´ ee qui ´ etait compatible avec la contrainte
budg´ etaire bleue passe en partie en dessous de la contrainte budg´ etaire rouge, ce qui prouve
que ce consommateur pourra, en recombinant sa consommation obtenir plus de bien-ˆ etre.
A retenir : cette am´ elioration de bien-ˆ etre n’est possible qu’` a travers un changement (radi-
cal) de la consommation du m´ enage.
2) Pr´ edire l’´ evolution de la consommation optimale de Linh entre la CB bleue et la CB
rouge : + ou - de bien 1, de bien 2 ?
On voit sur le dessin que la consommation optimale sera ` a droite de l’intersection des deux
contraintes budg´ etaires, donc, plus de bien 1 et moins de bien 2.
3 Calcul de l’´ elasticit´ e-prix de la demande
1) Quelle est l’´ elasticit´ e de la demande de cigarettes de Ricardo, sachant qu’il consomme
3 paquets de 25 cigarettes quand le paquet de 25 est ` a 15 FF et qu’il consomme 3 paquets
de 20 quand le paquet de 20 est ` a 20 FF. Pourquoi peut-on dire que c’est un grand fumeur ?
2

On doit rapporter l’´ elasticit´ e de la demande par rapport au prix d’une cigarette.
Avant : le prix d’une cigarette est 15/25=3/5=0,6FF
Apr` es : le prix d’une cigarette est 20/20=1FF
∆p
p= 1 −0,6/0,6=0,4/0,6=2/3
La demande est mesur´ ee en nombre de cigarettes :
Avant : 75 cigarettes
Apr` es : 60 cigarettes
∆q
q= (75 −60)/75 = −15/75 = −1/5
On a alors l’´ elasticit´ e par rapport au prix
εp=∆q
q/∆p p=−1 5∗3 2=−0,3
2) Ricardo rencontre un mouvement spirituel oppos´ e` a la consommation de tabac, qui lui
d´ evoile que la m´ editation est un tr` es bon substitut ` a la consommation de tabac. Alors qu’il
consommait 3 paquets de 25 cigarettes quand le paquet de 25 est ` a 15 FF, sa consommation
est pass´ e` a 2 cigarettes par jour quand chaque cigarette vaut 1FF. Quelle est son ´ elasticit´ e
apr` es qu’il ait admis qu’il existait un bon substitut ` a la cigarette. Auriez-vous pu pr´ evoir
sans calcul que cette nouvelle ´ elasticit´ e est tr` es grande en valeur absolue ?
Calculs similaires
∆p
p= 1 −0,6/0,6=0,4/0,6=2/3
∆q
q= (75 −2)/75 = −73/75
εp=∆q
q/∆p p=−73 75 ∗3 2=−1,46
Cette ´ elasticit´ e est d’autant plus grande que le consommateur a diminu´ e sa consommation
de cigarettes.
4 Compensation de revenu
1) Consid´ erez une vieille dame qui d´ epense sa retraite entre les d´ epenses li´ ees ` a sa vie
quotidienne simple et les d´ epenses qu’elle fait pour ses petits-enfants. On suppose que les
d´ epenses li´ es au logement peuvent ˆ etre mesur´ ees par une quantit´ e et on note p1le prix de
ce type de bien et x∗
1la consommation de ces biens par la vieille dame aux prix (p1, p2).
On mesure par ailleurs les d´ epenses en cadeaux donn´ es aux petits-enfants, par convention
on admet p2= 1 et on note x∗
2la consommation de ces biens par la vieille dame aux prix
3

(p1, p2). A supposer que le prix du bien 1 augmente de 10%, indiquez pourquoi la vieille
dame pourrait conserver la mˆ eme consommation si on lui donne en compensation de cette
augmentation de prix le revenu compl´ ementaire 0,1p1x∗
1. Justifier pourquoi la vieille dame
va modifier sa consommation ` a l’occasion de cette augmentation de prix si on lui donne le
revenu compl´ ementaire 0,1p1x∗
1.
Si on augmente le prix du bien 1 de 10%, pour consommer le mˆ eme panier de bien, la
grand-m` ere d´ epenserait (1,1p1)x∗
1+p2x∗ 2= 0,1p1x∗ 1+ [p1x∗ 1+p2x∗ 2] = 0,1p1x∗ 1+R;
elle le peut donc si on lui donne le revenu compl´ ementaire 0,1p1x∗
1.
Il est ` a remarquer que si on lui donne ce nouveau revenu, la vieille dame peut en effet
consommer de nouveau le panier (x∗
1, x∗ 2). Cependant, il est `
a remarquer que son TMS qui
n’a pas chang´ e, et qui ´ etait ´ egal ` ap1/p2devient diff´ erent du nouveau prix relatif du bien
1 en bien 2, ` a savoir 1,1p1/p2, et plus pr´ ecis´ ement inf´ erieur. Ceci ach` eve de prouver que
le panier (x∗
1, x∗ 2)n’est pas la consommation optimale de la grand m`
ere dans cette nouvelle
situation de prix et de revenu ; que la grand m` ere dans cette nouvelle situation de prix et de
revenu va consommer moins de ce bien 1 devenu plus cher.
2) Soit un m´ enage dont l’utilit´ e est U=√x1+x2. A supposer qu’initialement son
revenu initial est de R= 10 et que les prix des deux biens sont p1= 1/20 et p2= 1.
Quel est le revenu suppl´ ementaire qu’il faudrait lui donner pour compenser exactement une
augmentation du prix du bien 1 de 50% ?
Exercice difficile Pour y voir plus clair, il est utile de calculer la consommation optimale
de ce consommateur, dans la situation initiale, et dans la solution finale avec le revenu
R+δ. On ´ egalisera ensuite les utilit´ es dans ces deux situations optimales pour pouvoir
calculer pr´ ecis´ ement δ.
Consommation optimale initialement Tout d’abord, on calcule le TMS de ce m´ enage
U1=1
2√x1
U2= 1 T MS =1
2√x1
On recherche un panier qui est sur la droite budg´ etaire x1
20 +x2= 10 et qui ´
egalise le TMS
et le prix relatif du bien 1 en bien 2, soit 1
2√x1
= 1/20, ce qui conduirait ` a√x1= 10,
x1= 100 et x2= 10 −100
20 = 10 −5=5.
Le panier optimal initial est (100,5) qui conduit ` a l’utilit´ eUi=√100 + 5 = 15.
Consommation optimale avec le nouveau prix et le revenu 10 + ρ.On recherche un
panier qui est sur la droite budg´ etaire 1,5x1
20 +x2= 10 + δet qui ´
egalise le TMS et le prix
4

relatif du bien 1 en bien 2, soit 1
2√x1
= 1,5∗1/20 = 15/200 = 3/40, ce qui conduirait ` a
√x1= 20/3,x1= 400/9et x2= 10 + δ−400
20 ∗9= 10 + δ−20 9.
Ce panier conduit ` a l’utilit´ eUδ= 20/3 + 10 + δ−20
9=130 9+δ
Revenu compensatoire Le m´ enage est compens´ e quand
130
9+δ= 15 ⇐⇒ δ=145 −130 9=15 9= 5/3=1,40.
5 Question de cours (maximum 5 lignes)
Donner un exemple motiv´ e de m´ enages qui ont radicalement chang´ e leur consommation
quand la structure des prix s’est modifi´ e suite ` a un ´ ev` enement particulier.
5