Analyse fréquentielle et temporelle

Exercice 1 : Analyse fréquentielle et temporelle d’un système électrique
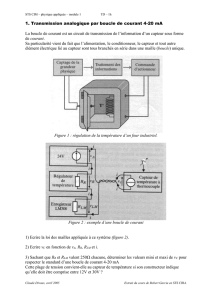
La figure suivante présente le schéma du montage pour relever expérimentalement la réponse d’un système de
type électrique à une excitation générée par un générateur de basses fréquences (GBF) :
1. Analyse fréquentielle
Le signal d’entrée est un signal sinusoïdal d’amplitude V
10
constante et de fréquence f variable (ω = 2πf) : V
1
(t)
=V
10
sin(ωt).
En régime permanent, le signal de sortie est aussi un signal sinusoïdal d’amplitude V
20
et déphasé de ϕ par
rapport à V
1
(t) :
V
2
(t) =V
20
sin(ωt +ϕ).
En faisant varier la fréquence du signal d’entrée, on a les résultats suivants :
Pulsation
ω
(rd/s)
V
20
/V
10
(décibel)
Déphasage
ϕ
( degrés )
0.10 -0.011 -2.86
0.16 -0.021 -4.68
0.27 -0.040 -7.64
0.44 -0.077 -12.40
0.72 -0.15 -19.80
1.18 -0.28 -30.51
1.93 -0.53 -44.00
3.16 -0.97 -57.70
5.18 -1.71 -68.90
8.48 -2.86 -76.74
13.90 -4.47 -81.81
22.76 -6.50 -85.00
37.28 -8.87 -86.93
61.05 -11.45 -88.13
100 -14.15 -88.85
1.1. Tracer dans le plan de Bode, de Black la réponse fréquentielle du système.
1.2. Justifier qu’il s’agit d’un système du premier ordre.
1.3. On admet que sa fonction de transfert peut s’écrire sous la forme suivante :
2
1
( )
( ) ( ) 1
V p K
H p
V p p
τ
= = +
.
Déterminer les paramètres K et τ en exploitant les courbes de réponses en fréquence.
1.4. La courbe gain seule, est-elle suffisante pour déterminer ces paramètres ?
1.5. La courbe de phase seule, est-elle suffisante pour déterminer ces paramètres ?
2. Analyse temporelle
On applique à présent un signal carré d’amplitude 0.5 v et de période 10s. La réponse est enregistrée sur
l’oscilloscope comme le montre la figure 4.55.
2.1. Justifier que la réponse temporelle confirme bien que le système étudié est du premier ordre.
2.2. Retrouver approximativement le gain statique K.
Oscilloscope
V
2
V
1
Circuit
électriqu
e
GBF

2.3. Retrouver approximativement la constante de temps τ par mesure du temps de réponse à 5 % en considérant
l’intervalle [0-5s].
3. Discussion
Les deux méthodes ont permis de déterminer expérimentalement les paramètres d’une fonction de transfert
susceptible de représenter le système étudié (Fonction de transfert d’ordre 1 de paramètre K et τ).
Quelle est à votre avis la méthode qui apparaît la plus commode ?
Exercice 2 : Tracé des lieux de transfert
Soit la fonction de transfert suivante :
3
)1(
1
)( Tp pG + =
; T = 0.5 s
1. Vérifier les expressions complexes de G(jω) :
2 2 2 2
2 2 3 2 2 3
2 2 3/ 2
1 3 (3 )
( )
[1 ] [1 ]
1
( ) 3 ( )
[1 ]
T T T
G j j
T T
G j Arctg T
T
ω ω ω
ωω ω
ω ω
ω
− −
= −
+ +
= −
+
2. En vous aidant de ces expressions, tracer le lieu de transfert G(jω) dans le plan de Bode, Black et Nyquist (
Pour le lieu de Nyquist, seule l’allure est demandée, mais en donnant le plus d’indications possibles :
intersections avec les axes, pulsations caractéristiques…).
Exercice 3 : Etude d’un système d’ordre 1
On considère un moteur électrique à courant continu et à excitation indépendante de fonction de transfert
inconnue notée M(p). On a réalisé l’expérience suivante :
Le tachymètre est une génératrice tachymétrique. Il constitue l’organe de mesure de la vitesse de rotation
(capteur de vistesse). Il délivre une tension proportionnelle à la vitesse de rotation; soit V = Kg Ω, avec Kg = 6
V/tours/s.
0 5 10 15
0
0.2
0.4
0.6
Temps( s)
Amplitude (v)
Ampli de puissance
+
Moteur Electrique
Capteur de vitesse
angulaire
« Tachymètre »
Kg
Générateur
de tension
continu
e
Um Ω
ΩΩ
Ω V

L’application de la tension U = 2 volts a donné la réponse indicielle indiquée par la figure 3.57
1. Analyse de la réponse
1.1. Préciser la vitesse en régime permanent
1.2. Expliquer l’origine probable des ondulations et le temps mort observé au démarrage du moteur.
1.3. Ce temps mort sera négligé et on propose de modéliser l’ensemble constitué par moteur et le capteur par une
fonction de transfert du premier ordre :
( ) ( )
( ) 1
V p K
G p
Um p Tp
= = +
Vérifier qu’on a approximativement K = 2.5 et et T = 5. Quelle est la dimension de chaque paramètre?
2. Etude en boucle fermée
Ce système est inséré dans une boucle d’asservissement comme il est montré sur la figure suivante où k est un
amplificateur de gain k strictement positif :
2.1. Calculer la fonction de transfert en boucle fermée V(p)/Uc(p)
2.2. Pour k = 1 et k = 5, déterminer la tension de consigne Uc dans le but d’obtenir la même vitesse de rotation
que précédemment (Fonctionnement en boucle ouverte).
2.3. Pour ces deux valeurs de k, déterminer le temps de réponse à 5%. Le comparer à celui de la boucle ouverte.
Conclusion.
2.4. La bande passante est définie par la pulsation de cassure. Pour les deux valeurs de k, déterminer la bande
passante en boucle fermée et la comparer à celle de la boucle ouverte. Conclusion.
Ampli
+
« Tachymètre »
Générateur
de tension
continue
Uc +
Ω
ΩΩ
Ω V
Um
k

Exercice 4 : Analyse statique et transitoire d’une régulation de niveau
Le dispositif de la figure 3.59 met en œuvre le réglage de niveau du liquide dans un réservoir. Le débit
d’utilisation Qu est perçu comme une perturbation et donc le but de la régulation est de maintenir le niveau
constant est égal à un niveau désiré h
ref
quel que soit ce débit d’utilisation.
Pour ce faire, le niveau h est mesuré indirectement par un capteur de pression situé au fond du réservoir. Ce
capteur délivre une tension y reliée à h par la relation :
1 1
( ) ( ) 8 /
y t h t avec v m
α α = =
La référence de niveau est fixée par une tension de référence y
ref
telle que y
ref
= α h
ref
; avec α = 8 v/m.
Le débit Qe est réglé par une vanne électromécanique dont la grandeur de commande est une tension u.
L’écart instantanée e(t) entre la tension de référence et la tension mesurée est traitée par un module électronique
élaborant une relation de correction et d’amplification de puissance ; il délivre la tension u à l’actionneur
(électrovanne), de sorte que u(t) = k e(t) ; où k est le gain de l’amplificateur. Le schéma fonctionnel de ce
dispositif de régulation est représenté par la figure 3.60.
1. Modélisation (Mise en équation)
Dans le but de déterminer la fonction de transfert de l’électrovanne (entrée u, sortie Qe), celle-ci est isolée. On
applique une tension constante de 10v. La réponse donnée par un débitmètre et enregistrée sur la figure 3.61.
Compte tenu de son allure, la fonction de transfert de l’ensemble (électrovanne + débitmètre) peut être
considérée du 1
er
ordre de constante de temps τ
2
et de gain statique k
2
:
2
2
( )
( ) 1
kv p
u p p
τ
=+
1.1. Relever à partie de la réponse le temps de réponse à 5%.
1.2. Sachant que le débitmètre fournit une tension proportionnelle au débit mesuré suivant la relation v(t) = k
v
Qe(t) avec k
v
= 0.25 10
4
v/m
3
/s. Vérifier qu’on a approximativement :
2
2
( )
( ) 1
Qe p
u p p
α
τ
=+
α
2
= 2 10
-4
m
3
/sv et τ
2
= 2 s.
u
Qu
Qe
Um
Uref
Electrovanne
+
h
h
max
Alimentation
Qu
y
e
u
Qe -
+
Uref +
-
h
Actionneur
Electrov
a
nne
Ampli
k
Réservoir
Capteur

1.3. Justifier que la fonction de transfert du réservoir (Entrée:Qe-Qu sortie h) est :
1
Sp
; où S est la section de
base. On donne S=0.05 m
2
.
1.4. Calculer en fonction de k, l’équation algébrique de y(p) sous la forme :
1 2
( ) ( ) ( ) ( )
ref o
y p F p y F p q p= +
2. Analyse statique de la régulation
2.1. En l’absence de toute perturbation, préciser en régime permanent (statique), le niveau atteint lorsque la
consigne est fixée à 0.5 m. En déduire le débit d’alimentation Qu et la tension de commande u.
Pour ce faire, il est recommandé de calculer le gain statique en boucle fermée ou d’utiliser le théorème de la
valeur finale pour calculer n’importe quelle variable en régime permanent suite à l’application de l’échelon de
consigne 0.5m
2.2. Le niveau h a atteint son état final. Une utilisation de l’eau consiste à soutirer l’eau avec un débit constant
Qu = 2. 10
-3
m
3
/s. Après l’extinction du régime transitoire, préciser le nouveau niveau atteint. En déduire la
variation du niveau observé.
2.3. Déterminer dans ce fonctionnement le débit d’alimentation Qe et la tension de commande u.
2.4. L’objectif de l’asservissement et de la régulation est-il parfaitement atteint ?
3. Analyse dynamique (transitoire)
Dans cette étude, on ne tient compte que de la fonction de transfert F
1
(p) (Etude en asservissement).
3.1. Ecrire la fonction de transfert F
1
(p) sous sa forme canonique :
2
2 2
( )
( ) ( ) 2
bf n
ref n n
K
y p
H p y p p p
ω
ξω ω
= = + +
en exprimant les paramètres ξ et ω
n
en fonction de k.
3.2. Comment faut-il choisir le coefficient d’amortissement ξ de manière à n’observer aucun dépassement
pendant le régime transitoire ? En fixant une valeur de votre choix, calculer la valeur de k compatible.
3.3. Dans le cas où un dépassement de l’ordre de 5% est tolérable, comment faut-il choisir k ?
3.4. Quel est le temps de réponse à 5% ?
3.5. Sachant que le niveau maximal à ne pas dépasser pour éviter tout risque de débordement est h
max
= 0.75m.
Quelle est la valeur de k qu’il ne faut pas dépasser sachant que la consigne sera fixée à 0.5m ?
Exercice 5 : Analyse temporelle et fréquentielle d’un servomécanisme
On reprend le servomécanisme étudié dans l’exercice 3