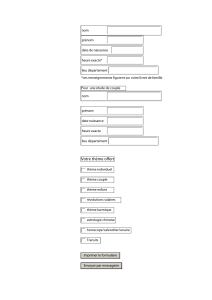
1°) ! 0 (en rad) Le schéma n `est pas à l`échelle. \ (en s) Données

A-
1°) !
0 (en rad)
Le schéma n 'est pas
à l'échelle.
\ (en s)
Données : • Masse du solide ponctuel : m=250 g • Période propre d'un pendule simple : T = 2n
Un pendule simple est formé par un solide ponctuel de masse m, fixé à un fil inextensible de longueur L et de masse négligeable.
Le pendule simple ainsi constitué est suspendu par son extrémité libre en un point fixe A. On écarte le pendule de la verticale
d'un angle 80, le solide ponctuel se situant au point P. On lâche alors le pendule sans vitesse initiale à la date t=0 et il effectue
des oscillations non amorties. On appelle abscisse angulaire l'angle orienté 8 que fait le pendule avec la verticale. On enregistre les
variations de l'abscisse angulaire 6 en fonction du temps t, au cours des oscillations. On négligera tous les frottements et on prendra
pour référence de l'énergie potentielle de pesanteur Epp, le point E correspondant à la position d'équilibre du solide ponctuel.
I
Parmi les affirmations suivantes, combien y en a-t-il d'exactes ?
• La valeur de l'angle 60 est égale à 15°.
• La période T des oscillations du pendule simple a pour valeur T=l,4 s.
• La longueur du fil est L=49 cm.
• La valeur de l'énergie potentielle de pesanteur au point P est EPP=53 mJ.
» La valeur de la vitesse du solide ponctuel au passage par sa position d'équilibre est VE=0,65 m.s"1.
a : 1 b : 2 c : 3 d : 4 e:5 f: aucune affirmation exacte
2°) (Suite de la question précédente)
Calculer la valeur de la tension F (en N) exercée par le fil sur le solide ponctuel au passage par le point E, lors des oscillations.
a: 2,5 b : 2,7 c: 3,1 d : 3,3 e : 3,7 f: aucune réponse exacte
3°)
Le schéma n 'est pas
à l'échelle.
A la date t=0, on lance un projectile, considéré comme ponctuel,
à partir d'un point O avec une vitesse initiale V0 faisant un angle a
avec l'horizontale.
L'objectif d'une caméra est placé dans un plan horizontal situé à une
hauteur H au dessus du sol.
Le projectile passe lors de son mouvement ascendant dans le plan de
l'objectif à l'instant t, puis lors de son mouvement descendant à l'instant t2.
On négligera l'action de l'air sur le projectile.
Données :
* V0=10,5m.s-' «0=42,3° • At=trt,=l,02 s
Calculer l'altitude H (en m) à laquelle se situe l'objectif de la caméra.
a: 1,12 b: 1,27 c: 1,48 d: 2,41 e: 2,54
f : aucune réponse exacte
4°) Le système GPS est composé d'une constellation de 24 satellites, chaque satellite étant équipé de plusieurs horloges atomiques.
Pour calculer la position de l'utilisateur, il faut prendre en compte les effets relativistes.
On se limitera ici au phénomène de dilatation des durées : l'horloge du satellite va retarder par rapport à la même horloge
située sur Terre. On admettra qu'un satellite GPS est en orbite circulaire à l'altitude h=20200 km.
Données : • Masse de la Terre : Mx=5,97* 10" kg • Rayon de la Terre : RT=6,37*103 km
• Constante de gravitation universelle : G=6,67xl0~u m3.kg"'.s"2 . At^.At,, avec y = •
• Célérité de la lumière dans le vide : c=3,00* 108 m.s'1
At,„ : durée mesurée
Atp : durée propre
Calculer la dérive journalière (en fis) de l'horloge atomique du satellite par rapport à la même horloge sur Terre.
a : 7,2 b : 8,2 c : 9,5 d : 10 e: 15 f: aucune réponse exacte Page : 1/4

5*)AJUti réacteur nucléaire fonctionne à l'aide d'uranium enrichi en isotope 235.
Les noyaux d'uranium 235 subissent différentes fissions, parmi lesquelles Tune des plus fréquentes est la suivante :
'STe+8Zr+3in
w u + 0n-
Itpihr
• Masse d'un neutron : ny*] ,00866 u
• Unité atomique : lu-1,66054x10"" kg
• Célérité de la lumière dans le vide : c=2,9979x 10» m.s-'
• l eV-l,6022xl(r"J
• Constante d'Avogadro : NA«6,022xlO" mol-1 masse molaire de l'uranium 235 : M-235 g.mol*'
Calculer l'énergie libérée (en MeV) au cours d'une fission.
«: 152,4 b: 168,2 c: 176,3 d; 1863 e; 194,3 f: aucune réponse exacte
•
noyaux
235IT
92U
95 7R I38T>
S2ie
masse (en u)
234,9933 94,8860
137,9007
5°) (Suite de la question précédente)
t>) On suppose que toutes les fissions nucléaires de l'uranium 235 libèrent la même énergie que précédemment
Chaque jour, le réacteur nucléaire consomme une masse m*l 12 kg d'uranium enrichi qui contient 3,0 % en masse d'uranium 235.
La puissance électrique produite par le réacteur nucléaire est de 920 MW.
Le rendement du réacteur est défini par :
PE : puissance électrique fournie par le réacteur
PN : puissance nucléaire fournie par toutes les réactions de fission de l'uranium 235
Déterminer la valeur do rendement i\n %) do réacteur.
a: 29 b: 31 c: 33 d : 35 e: 42
f: aucune réponse exacte
5°) jLe point A d'un objet AB réel est placé sur l'axe optique d'une lentille convergente de vergence Ol5 S.
1
L'objet AB, assimilable i un segment, est perpendiculaire à l'axe optique de la lentille.
L'axe optique est orienté dans le sens de la propagation de la lumière.
Le centre optique de la lentille est noté O. L'image de l'objet AB formée par la lentille est notée A'B*.
L'image A'B' est virtuelle, de même sens et quatre fois plus grande que l'objet AB.
Calculer la valeur algébrique de la distance A'A (en cm).»
a; -15 b: -10 c : -5 d: 10 e: 15 aucune
réponse exacte pagc • 1/4

6*) On réalise un pendule électrostatique en reliant une sphère métallique
de masse m, à l'extrémité inférieure d'un fil inextensible, de masse
négligeable et de longueur L. L'extrémité supérieure du fil est fixée en
un point P. La sphère métallique, de petite dimension, sera considérée
comme ponctuelle et portant la charge électrique q.
On place la sphère métallique entre les armatures verticales A et B d'un
condensateur plan non chargé.
La distance entre les armatures A et B est notée d.
La sphère métallique se trouve alors au point O, situé à égales distances
des armatures A et B (voir schéma).
On se placera dans le repère orthonormé (O, i, j).
On applique une tension U ^ entre les deux armatures A et B.
Il règne alors un champ électrostatique uniforme E entre les deux armatures.
Le pendule électrostatique prend une position d'équilibre, en s'écartant
de la verticale d'un angle a et la sphère se situe en un point M.
Données:
• La direction du champ électrostatique E est perpendiculaire aux armatures.
• Le sens du champ électrostatique Evade l'armature positive vers l'armature négative.
• La valeur E du champ électrostatique à l'intérieur d'un condensateur plan se calcule par la relation : E • !
• La sphère est soumise à l'intérieur du condensateur plan à la force électrique : F = qË, u
•UAB-LOKV q»-15uC
• L-25 cm d=l2 cm
• m=27 g
Déterminer les coordonnées (xM ; yM) (en cm) du point M.
a: (-10,7; 2,4) b: (-10,7; 3,8) e: (0,0) d: (10,7; 2,4) e: (10,7; 3,8) f: aucune réponse exacte
A
P
B
ï -
1
1 i
X
•
O
d
Le schéma n'est pas a l'échelle.
U
AB
7°) La lame métallique d'un vibreur, fixée en l'extrémité O d'une corde tendue horizontalement, génère une onde progressive sinusoïdale
de fréquence f. L'onde se propage le long de la corde avec une célérité v. A l'autre extrémité de la corde, on a installé un dispositif
anti-réflexion. Le graphique n° 1 donne les variations de l'ordonnée y0 du point O en fonction du temps t et le graphique n°2
représente l'aspect de la corde, à un instant t,. L'origine des abscisses x correspond au point O.
Parmi les affirmations suivantes, combien y en a-t-ii d'exactes ?
* La fréquence de l'onde est de 100 Hz.
• La longueur d'onde est égale à 20 cm.
• La célérité de l'onde est v-1,5 m.s'1.
• L'amplitude du mouvement du point O est égale i 4 cm.
• L'onde est une onde mécanique, périodique, transversale.
• cl b:2 et 3 d: 4 e: 5 f: aucune affirmation exacte
8") fSuite de la question précédente)
Sur le graphique n*2, la corde a été représentée à un instant t,.
On propose ci-dessous différentes valeurs pour t, dont certaines ne sont pas possibles :
ct-50 ms ; P» 100 ms ; y -150 ms ; 8= 200 ms ; e- 250 ms.
Indiquer parmi les valeurs ci-dessus, celles qui ne peuvent pas correspondre à cet Instant t,.
a: (ot;P) b:(o;y) cr(B;y) d:(p;5) e: (a;e) f: aucune valeur exacte
Pane : 2/4

9*) Le spectre d'émission de l'atome de mercure présente une raie ultraviolette de longueur d'onde X.-254 nm.
Les raies du spectre de l'atome de mercure résultent des transitions entre ses différents niveaux d'énergie.
Le diagramme ci-contre représente, sans souci d'échelle, certains niveaux d'énergie de l'atome de mercure.
E0 désigne l'état fondamental de l'atome de mercure, c'est-à-dire son niveau de plus basse énergie.
Données :
• Constante de Planck : 0-6,63x10** J.s
• Célérité de la lumière dans le vide : cS.OOxlO* m.s'1
•leV~l,60xl<r"J
Déterminer la transition énergétique responsable de la raie ultraviolette.
a : E,—» Eo b : Ej-» Eo c : Ej—» d : Ej-* E, e : E4-+ E,
0
-3,73.
-4,98.
-5,55
-5,77
-10,44
E. (en eV)
—B,
-E,
-E,
f : aucune réponse exacte
• vOnkm.h'1)
10") Un mobile se déplace suivant une trajectoire rectiligne.
Le graphique ci-contre dorme les variations de ta vitesse du mobile
en fonction du temps au cours du mouvement
Calculer la distance parcourue (en km) par le mobile sur l'ensemble de son mouvement
• : 6,7 b: 7,7 c: 9,7 d: 10,4 e: 11,7 f: aucune réponse exacte
t (en min)
Exercices : (10 points) Répondez aux questions en expliquant brièvement votre démarche.
Eil :( 5 points)
Un solide ponctuel S de niasse M est abandonné sans vitesse initiale d'un point P situé au sommet d'un plan incliné PO.
Ce plan PO est incliné d'un angle a par rapport à l'horizontale.
Le solide S glisse suivant la ligne de plus grande pente du plan incliné.
Le solide S est soumis sur le plan incliné à une force de frottement s'opposant au mouvement et de valeur constante, notée f.
On notera L-PO la distance parcourue par le solide S sur le plan incliné.
Le solide quitte le plan incliné en O puis effectue un mouvement aérien.
La réception du solide S a lieu sur un deuxième plan BC, incliné d'un angle P par rapport & l'horizontale.
Le point B est situé sur la verticale passant par le point O.
Le point de contact du solide S avec le plan BC est noté I (voir schéma).
On se placera dans le repère orthonormé (O, i, j).
On négligera l'action de l'air sur le solide pendant toutes les phases du mouvement.
Le solide sera considéré en chute libre pendant la phase aérienne du mouvement.
P
•M-450g
y
1*) Déterminer l'expression de l'accélération a du solide S sur le plan PO en fonction de g, a, f et M.
2*) Calculer la valeur v0 (en nu'1) de m vitesse du solide S an point O.
3*) Etablir l'équation cartésienne de la trajectoire de S, dans le repère (O, ï, j), Ion de la phase aérienne du
mouvement On exprimera cette équation en fonction de g, a et v„.
4*) Calculer les coordonnées (x, ; y,) (en m) du point I.
5°) En déduire la valeur de la distance BI (en m). !