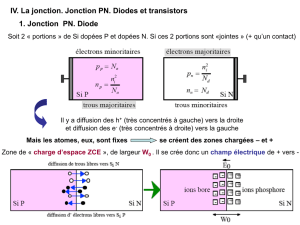
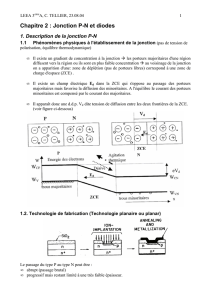
Rappels sur la physique des composants Jonction PN

Centre d’Electronique et de
Microoptoélectronique de Montpellier
(CNRS UMR 5507)
UNIVERSITE MONTPELLIER II
SCIENCES ET TECHNIQUES DU LANGUEDOC
Place E. Bataillon - 34095 - Montpellier - Cedex 5 - France
Tél : [phone] - Fax [phone]
e-mail : [email protected]
M2 STPI EEA / IUP GEII
UMSIE301
COMPOSANTS ELECTRONIQUES
Rappels sur la physique des composants
Jonction PN
Fabien PASCAL

1
Rappels sur la physique des composants
Introduction
Nous allons ici reprendre les notions fondamentales de physique du semiconducteur. Il
ne s’agit pas d’une présentation complète, mais plutôt par le biais de rappels de souligner les
paramètres physiques et électriques qui entrent en jeu dans l’étude des composants utilisés en
électronique intégrée tout en soulignant leur importance en tant que limitations
technologiques .
Classiquement un cours sur la physique des semiconducteurs commence par une étude
de la structure cristalline avec une approche quantique (l’électron dans un puits de potentiel
avec la notion fonction d’onde, d’énergie quantifiée, théorème de Bloch, concept de masse
effective…). Nous nous contenterons d’utiliser certains résultats issus de ces études comme la
notion de bandes d’énergie, les statistiques de distribution. Ce cours portera sur les propriétés
électroniques des semiconducteurs (à l’équilibre et hors équilibre thermodynamique), sur la
jonction et l’hétérojonction p-n et enfin sur le transistors bipolaire et le transistor bipolaire à
hétérojonction (le transistors MOS est présenté par M. Valenza).
Références bibliographiques :
Physique des semiconducteurs et des composants électroniques, H. Mathieu, Masson
Semiconductor Physics&Devices, D.A. Neamen, Irwin
Dispositifs et circuits intégrés semiconducteurs, A. Vapaille et R. Castagné, Dunod
I Mouvement des porteurs de charge dans les solides
EqF −=
Courant de conduction :
I = nSqv
t
nLSq
t
Nq
t
Q=== (v : vitesse moyenne des porteurs)
J= nqv
Conductivité, mobilité :
+
+
+
+
+
+
-
-
-
-
-
V
E
+
-
L

2
I =
R
V E = L V R = S L
ρ ⇒ J = σE avec σ =
ρ
1
σ = E
nqv soit µ = E v = mobilité électronique alors σ = nqµ
J =
σE = nqµΕ
Généralisation (électrons et trous) :
I
total = IpIn + → σtotal = q (nµn +pµp)
Courant de diffusion :
Lié à un gradient de concentration : les porteurs de charge se déplacent afin de se
répartir uniformément dans le matériau. Ce courant est régi par les lois de Fick.
n gradDn qJ∆n=
r→ dx
dn(x)
Dn qJ∆n= dans une structure unidimensionnelle
p grad Dp qJ p−=
∆
r
→ dx
dp(x)
Dp qJ∆p−=
avec Dn et Dp les coefficients de diffusion des électrons et des trous
respectivement.
Relations d’Einstein :
Dans un SC isolé : Jcond +Jdiff = 0 d’ou
q
kT
µ
Dn
n
= et q
kT
µ
Dp
p
=
II Le semiconducteur à l’équilibre thermodynamique
1) Le semiconducteur intrinsèque
Diagramme de bandes d’énergie :
W0 = énergie de libération
Bande de conduction → e- libres
Bande de valence → e- liés
Bande interdite pas d’e- → Eg = Ec - Ev
Eg
Niveau du vide
Ws = énergie de sortie → qχ (χ affinité électronique)

3
Conductivité :
n = p = ni
σ = q (nµn +pµp) = q ni (µn +µp) avec ni = 2kT
Eg
2
3
eAT −
Distribution des porteurs de charges :
Soit dn le nombre d’e- ayant une énergie comprise entre E et E+dE :
dn = Nc(E) fn(E) dE avec Nc = densité d’état, représente le nombre de place
disponible et fn(E) la statistique d’occupation.
Ainsi le nombre total d’e- n est :
n =
∫
∞
Ec
(E)dENc(E)fn
Pour un SC non dégénéré on applique la statistique de Boltzman ainsi on
montre que :
n = kT
EE
C
FC
eN
−
− avec NC et NV densité équivalente d’état de la bande de
conduction et de la bande de valence respectivement. EF
est le niveau de Fermi.
p = kT
EE
V
FV
eN
−
NC = 2
3
2
e)
h
kT2m
(2
π
et NV = 2
3
2
p)
h
kT2m
(2
π
Produit np :
np = NCNV kT
Eg
e− produit constant ne dépend que des
caractéristiques du matériau SC
pour un SC intrinsèque
np = ni2 → ni = 2kT
Eg
2
1
VC e)N(N −
Position du niveau de Fermi :
n = p → EF =
C
VVC
N
N
ln kT
2
1
2
EE +
+
≈ 2
EE VC
+
2) Le semiconducteur extrinsèque

4
dopage n ou p d’un SC
Type N (basse température) Type P
Equation de neutralité :
n + N
Ai = p + NDi → à 300K n + NA = p + ND
Loi d’action de masse :
np = n
i2
Type N :
N
D >> NA n (majoritaires) >> p (minoritaires) → n = ND et p =
D
2
i
N
n
Type P :
N
A >> ND p >> n → p = NA et n =
A
2
i
N
n
Niveau de Fermi :
Dopage n : EFn = EC – kT ln
D
C
N
N
Dopage p : EFp = EV + kT ln
A
V
N
N
Distribution des porteurs de charges :
n = n
i kT
EE FiFn
e
−
majoritaires type N
p = n
i kT
EE FiFp
e
−
− majoritaires type P
III Le semiconducteur hors équilibre (régime variable)
1) Génération-Recombinaison
g’ = taux de génération de porteurs = nombre de particules crées dans une unité de volume
pendant une unité de temps
r’ = taux de recombinaison
La variation du nombre de porteurs par unité de volume et de temps s’écrit :
N
EC
EV
N
NDi
EC
EV
NAi