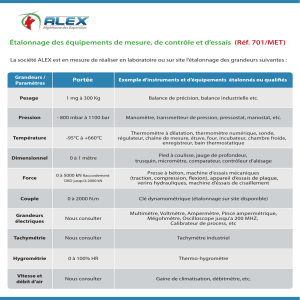
Donc, lorsqu`une grandeur est proportionnelle à plusieurs autres

ALGÈBRE ÉLÉMENTAIRE. 233
Donc, lorsqu'une grandeur est proportionnelle à plusieurs
autres grandeurs, elle est proportionnelle à leur produit.
S'il n'entre dans la question que les grandeurs x, P et Q, on
a évidemment
x = -p—- ou x. PQ = K.
Donc, lorsqu'une grandeur est inversement proportionnelle à
plusieurs autres grandeurs, elle est aussi inversement propor-
tionnelle à leur produit. -
39. Si l'on met la formule générale
/ «" b" p' q'
•A, .A- . ,
a' b p q
sous la forme x".a'. b'. p". q" — x'. a", b". p'. q', on peut remar-
quer que cette formule est homogène, c'est-à-dire que les
termes qui y entrent sont du même degré, puisqu'ils con-
tiennent le même nombre de facteurs littéraux à la même
puissance. Il doit en être ainsi toutes les fois qu'il s'agit de
relations algébriques entre grandeurs, lorsqu'aucune d'elles n'a
été prise pour unité spéciale. Nous reviendrons plus loin sur
le principe général de Y homogénéité, qui a une grande im-
portance (*). Partages proportionnels.
60. Partager un nombre N en parties x, y, z, proportion-
nelles aux nombres donnés a, b, c, c'est, d'après ce qui pré-
cède, vouloir qu'on ait
x r z
— = v = — = const.
« b c
Si l'on pouvait déterminer cette quantité constante, le problème
serait immédiatement résolu. Il suffît de se rappeler que lors-
qu'on ajoute plusieurs rapports égaux terme à terme, on forme
un rapport égal à chacun d'eux. La constante cherchée est
donc aussi égale au rapport
x + y+-z
a + b -i- c
Mais les trois parties x, y, z, forment le nombre N. On a donc
x y z N
a b c a + b -f- c
''* ) Tout ce que nous venons de dire sur les grandeurs proportionnelles ou
inversement proportionnelles est susceptible d'applications très-nombreuses
Nous en donnerons des exemples. Vous recommandons spécialement 1 étude de
cette théorie aux élèves