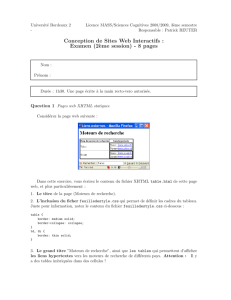
Théorie du consommateur Classiques: les biens ont une utilité ou

Th´eorie du consommateur
Classiques: les biens ont une utilit´e ou une valeur d’usage et une
valeur d’´echange. Paradoxe de l’eau et du diamand.
Smith A. (1776), An Inquiry into the Nature and Causes of the Wealth
of Nations
1705: machine `a vapeur, d´ebut de la r´evolution industrielle.
Marginalistes
Gossen H. (1854), Entwickelung der Gesetze des menschlichen Verkehrs
und der daraus fliessenden Regeln f¨ur menschliches Handeln
1) Premi`ere loi de Gossen: l’utilit´e marginale est d´ecroissante:
Utilit´e additive directe. Exemple:
u=a1ln q1+a2ln q2+...+amln qm
∂u
∂qi=ai qi>0 ; ∂2u
∂q2
i
=−ai
q2
i
<0
2) Deuxi`eme loi de Gossen: une personne maximise son utilit´e lorsqu’el-
le distribue l’argent dont elle dispose, pour l’achat des diff´erents biens,

de mani`ere `a obtenir la mˆeme satisfaction avec le dernier atome de mon-
naie d´epens´e pour chaque bien. Nous verrons ci-dessous l’interpr´etation
de cette loi.
Edgeworth et Pareto proposent une fonction d’utilit´e o`u l’utilit´e margin-
ale d’un bien d´epend aussi de la quantit´e consomm´ee d’autres biens.
Edgeworth F. (1881), Mathematical Psychics
Pareto V. (1909), Manuel d’´economie politique
Walras L. (1874), El´ements d’´economie politique pure
On a alors:
u=f(q1, q2,...,qm)
Par exemple:
u=qa1
1qa2
2...qam
m
On peut exprimer math´ematiquement la d´ecision du consommateur de
la mani`ere suivante:
max u =f(q1, q2,...,qm)
S.C. y =p1q1+p2q2+...+pmqm

En utilisant les vecteurs q= [qi] et p= [pi] ; i= 1,2, . . . , m , on peut
´ecrire:
max u =f(q)S.C. y =pTq
Le lagrangien est:
L=f(q1, q2,...,qm) + λ(y−Ppjqj)
o`u y est le revenu du consommateur.
Les conditions de premier ordre sont:
∂L
∂qi=∂u ∂qi−λpi= 0 i= 1,2,...,m
∂L
∂λ =y−Ppjqj= 0
En prenant deux ´equations quelconques iet j, on a:
∂u
∂qi/pi=λ;∂u ∂qj/pj=λ
∂u
∂q1
1
p1=∂u ∂q2
1
p2=...=∂u ∂qm
1
pm=λ
C’est la deuxi`eme loi de Gossen. En effet:
∂L∗
∂y =∂u∗ ∂y =λest l’utilit´e marginale du revenu. L’utilit´e marginale de
chaque bien, pond´er´ee par son prix, doit ˆetre ´egale `a l’utilit´e marginale
du revenu.

La condition de deuxi`eme ordre pour un maximum est:
xTHx ≤0S.C. (∂u
∂q )Tx= 0 o`u
∂u
∂q = [ ∂u ∂qi] (i= 1,2,...,m) et
H=∂2u
∂qi∂qj(i, j = 1,2,...,m)
est la matrice hessienne de la fonction d’utilit´e. Il s’agit d’une matrice
sym´etrique (th´eor`eme de Young). Si la fonction d’utilit´e est additive di-
recte, alors la matrice hessienne est une matrice diagonale avec les vari-
ations de l’utilit´e marginale sur la diagonale. Toutes ces valeurs ´etant
n´egatives selon l’hypoth`ese de l’utilit´e marginale d´ecroissante, la ma-
trice hessienne est une matrice d´efinie n´egative et alors la condition de
deuxi`eme ordre est satisfaite (xTHx < 0 pour tout xet alors aussi
pour ( ∂u
∂q )Tx= 0). La premi`ere loi de Gossen permet de satisfaire la
condition de deuxi`eme ordre lorsque l’utilit´e est additive directe. Dans
le cas g´en´eral, la condition ci-dessus peut ˆetre v´erifi´ee en calculant les
d´eterminants suivants:

|HB
i|=
f11 f12 . . . f1i−p1
f21 f22 . . . f2i−p2
... ... ... ... ...
fi1fi2. . . fii −pi
−p1−p2... −pi0
i= 2,3,...,m avec fij =∂2u
∂qi∂qj
Il faut que:
|HB
2|>0 ; |HB
3|<0 ; ...(−1)m|HB
m|>0
Si la fonction d’utilit´e est strictement quasi-concave, alors cette condi-
tion est satisfaite. Une fonction est strictement quasi-concave si pour
tout q16=q2, on a:
f[λq1+ (1 −λ)q2]> min {f[q1], f[q2]}
0< λ < 1
avec qi= [qi
1, qi
2,...,qi
m]
Si
|HB
2|>0 ; |HB
3|<0 ; ...(−1)m|HB
m|>0