VIBRATIONS ELECTROMECANIQUES (

__________________________________________________________________________________________
Vibrations électromécaniques - 1
Plate-forme3E (Électricité, Electronique, Electrotechnique C.E.S.I.R.E. – Université J.Fourier Grenoble
VIBRATIONS ELECTROMECANIQUES
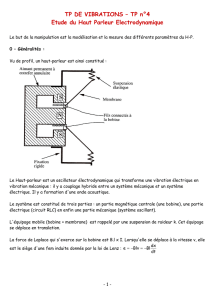
Les capteurs transformant la variation dans le temps d'un paramètre mécanique en une tension
électrique (ou inversement) sont appelés des transducteurs électrodynamiques. Ils reposent sur le
même principe que le haut-parleur électrodynamique. Le transducteur étudié est constitué d'une
bobine fixée sur une lame vibrante, qui se déplace dans un aimant cylindrique creux.
I(t) = I0 sin ω t
1 - Partie théorique
Le système comportant une bobine mobile (self), formée d'un fil de longueur l, liée à un oscillateur
mécanique (ressort ou lame vibrante) est régi par un système de 2 équations :
- équation mécanique
md2x
dt2+αdx
dt+k x =F(i)+F(t)
où
F(i)=il×B( )
est la force de Laplace et F(t) une force appliquée.
- équation électrique
Ldi
dt+RLi+1 Cidt=edx dt
∫+e(t)
où
edx
dt
est une f.e.m. induite par le mouvement de la bobine :
edx
dt
= −l B dx
dt
( Loi de Lenz)
et e(t) est la tension électrique appliquée au système.
L'impédance du transducteur est définie par ZAB = A + j.B = Z0 ejΦ
En utilisant les impédances électriques et mécaniques, calculer cette quantité lorsque F(t) = 0. (le
mouvement est produit par la seule énergie électrique).
Montrer que l'impédance ZAB se décompose en une partie liée aux seuls éléments électriques Ze et
une partie liée au mouvement Zm ( impédance motionnelle):
A=RL+AmB=Lω − 1
Cω
+m
B

__________________________________________________________________________________________
Vibrations électromécaniques - 2
Plate-forme3E (Électricité, Electronique, Electrotechnique C.E.S.I.R.E. – Université J.Fourier Grenoble
Montrer que, dans le plan complexe, l'extrémité du vecteur Zm décrit un cercle (cercle de Kennelly
) quand la fréquence de e(t) varie (faire les approximations nécessaires).
Donner les caractéristiques de ce cercle : position du centre et rayon.
Remarque : pour établir la formule de l'impédance, on prend comme quantité réelle toute quantité
qui exprime une dissipation d'énergie.
2 - Partie expérimentale
On place la bobine, montée sur une lame vibrante, en série avec une résistance R (1000 Ω est une
bonne valeur).
Pour chaque fréquence, les mesures successives de la tension aux bornes du circuit, aux bornes de R
et aux bornes de la bobine permettent de calculer l'impédance aux bornes de la bobine à cette
fréquence.
En balayant en fréquence dans un domaine de quelques hertzs autour de la fréquence de résonance,
on vérifiera que Zm décrit un cercle. On vérifiera également que loin de la fréquence de résonance
Zm est nul.
2-1) Rechercher manuellement la fréquence de résonance mécanique de cet oscillateur.
2-2) Sans utiliser le bus IEEE,
pour une fréquence proche de la fréquence de résonance, mesurer les tensions indiquées ci-dessus.
En utilisant un diagramme de Fresnel, en déduire la partie réelle et imaginaire de l'impédance totale
de la bobine.
2-3) Utilisation des programmes en Pascal "Oscilemg" et "Kennelly"
On réalise 2 séries de mesures permettant d'observer l'évolution de l'impédance au voisinage de la
résonance et loin de celle-ci .
a) Choisir un domaine de fréquence de quelques hertzs autour de la fréquence de résonance.
Le parcourir par pas de 0,2 Hz.
- Comparer les valeurs des composantes réelles et imaginaires de l'impédance aux bornes de la
bobine aux valeurs que vous avez calculées en 2-2.
- La courbe tracée au voisinage de la résonance est-elle un cercle ? Déterminer son centre. En
déduire la résistance et l'inductance de la bobine. Conclusion.
- Prévoir l'impédance totale et l'impédance motionnelle pour 1000Hz.
b) Choisir un domaine de fréquences de 200 à 5000 Hz . Le parcourir par pas de 400 Hz. En
déduire l'impédance totale et l'impédance motionnelle. La vérifier par mesure utilisant un montage
de résonance série. Comparer la courbe obtenue et la courbe théorique.
Comment expliquer l'évolution de la résistance et l'inductance loin de la résonance?

__________________________________________________________________________________________
Vibrations électromécaniques - 3
Plate-forme3E (Électricité, Electronique, Electrotechnique C.E.S.I.R.E. – Université J.Fourier Grenoble
3 - Utilisation du Bus IEEE
Le bus IEEE, commandé par un micro-ordinateur, est un "central téléphonique" à travers lequel
transitent les informations en provenance et à destination des différents appareils. Il assure et
contrôle la transmission des informations entre les divers appareils et le micro-ordinateur.
A chaque appareil est affecté "un numéro d'appel" c'est-à-dire une adresse.
Chaque appareil peut recevoir des informations ou en envoyer.
On programmera en Basic l'acquisition d'une seule valeur de chacune des trois tensions lorsque le
circuit est alimenté sous une tension donnée (Les instructions nécessaires sont répertoriées dans une
fiche disponible dans la salle de manip).
Réalisation du programme (programmer c'est traduire une série d'opérations et expliciter l'ordre
dans lequel elles doivent être exécutées)
Faire l'organigramme (suite logique des opérations à effectuer) des différentes opérations à réaliser
dans l'ordre voulu pour effectuer une mesure.
Avec le matériel disponible, effectuez manuellement les opérations décrites précédemment et
uniquement celles décrites; ceci doit vous permettre de vérifier si vous avez décrites toutes celles
qui sont nécessaires pour effectuer les mesures et dans le bon ordre.
Traduire ces différentes opérations en utilisant le langage proposé (Basic). Ce programme doit
permettre l'acquisition des données pour une seule fréquence.