23. Interprétation clinique des mesures de l`effet

23.
Interprétationcliniquedesmesuresdel’effet
traitement
23.1.Critèresdejugementbinaires
Plusieursmesures(indices)sontutilisablespourquantifierl’effet traitement lorsde
l’utilisation d’un critèredejugementbinaire.Cesmesures,risquerelatif,rapportdes
cotes(«odds-ratio»)etdifférence derisque,auxquelles s’ajoutelenombredesujets
qu’il faut traiterpouréviterun événement(NST), nevéhiculentpasexactement la
mêmeinformation clinique[182, 183].Ainsi,ellesnedonnentpasexactement les
mêmesrenseignements surlapertinence cliniquedel’effet.
Lesdeux premières(rapportdescotes,risquerelatif) sontdesmesuresrelatives
etestimentun bénéfice relatif,tandisquelesdeux dernières(différence desrisques
etNST)mesurentun bénéfice absolu.
Tableau23.2. — Terminologie.Relation entrelesmesureset letypedu bénéfice
MesuresModèled’effetIntérêt
Bénéfice
absoludifférence des risques,
NST
additif
(mesure additive)approchepragmatique (santépublique,
décision)
Bénéfice
relatifrisquerelatif, rapportdes
cotes
multiplicatif
(mesure
multiplicative)
approche explicative
(recherche)
Deplus,enméta-analyse,àceproblèmed’interprétation cliniquesesuperpose
celuide choixdumodèled’effet(voirchapitre31).
Uneréduction relativederisquede30%estdéjàuneréduction conséquente, qui
d’ailleursn’estquetrèsrarementobservée.Malgré cela,lapertinence cliniquede
ceteffetdépend du risquedebase.Eneffet,réduire enrelatifde30%un événement
fréquentestbien plusintéressantderéduiredanslamêmeproportion un événement
rare.Si lerisquedebase estde50%,sousl’effetd’uneréduction de30%,il devient

2
4
8
Interprétation cliniquedesmesuresdel’effet traitement
35%, donnantunedifférence derisquede15%.Avec un risqueinitialde5%,la
mêmeréduction relative aboutit àun risquesoustraitementde3,5%,correspondant
àunedifférence absoluede1,5%.Entermed’événementsévitéspour1000 sujets
traités,lepremiercasdefigure correspond à150 événementsévités,tandisquele
second àseulement15. Aussibien du pointdevuedelasantépublique, quedu point
devueindividuel,lapremièresituation estplusintéressantequelaseconde.
Exemple23.1 Letableau présenteles résultatsobtenusdans3essaisthérapeu-
tiques:l’essai4S [20],WestofScotland [15],etISIS 2 [55].Lesdeuxpremiers
essaisétaientdesessaisdeprévention delamorbi-mortalitéliée auxmaladiescar-
diaquesischémiques(infarctus)pardesmédicamentshypocholestérolémiantsdela
classedesinhibiteurs del’HMGCoAréductase(statines).L’essai4S était un essai
deprévention secondairedont la population cible estreprésentée parles sujetsqui
ont fait un premierinfarctusdu myocarde etoù lebutestdeprévenirles récidives.
L’essaiWestofScotland était parcontreun essaideprévention primaire.Cetype
deprévention s’adresseà des sujets sansantécédentsd’infarctuseta pourbutde
prévenirlasurvenued’un infarctus.Letroisième essaiévaluait lafibrinolyseintra-
veineuseàla phaseaiguëdel’infarctusdu myocarde.Danscestroisessaisle critère
dejugementétait lamortalitédetoutescauseset lespatientsdu groupe contrôle
recevaientun placebo.
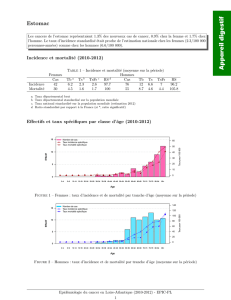
Nombrededécès(%) Durée Risque
Groupe contrôleGroupetraitédesuivirelatifDRNST
4SNombrededécès256 (11,5%) 182 (8,2%) 4,9 ans0.71 3.3%30
Effectif 2223 2221
WestofScotland
Nombrededécès135 (4,1%) 106 (3,2%) 5,4 ans0.78 0.9%112
Effectif 3293 3302
ISIS2
Nombrededécès(12,0%)(9,2%) 5semaines0.77 2.8%36
Effectif 8595 8592
Ilsetrouve queles risques relatifsobtenusdanscestroisétudes sontsimilaires.
Cependant,les risquesdebaseobservésdanslesgroupescontrôlesétant trèsdiffé-
rents(4Saunrisquedebasedeuxfois supérieuràceluideWestofScotland etproche
de celuid’ISIS2),lesvaleurs dedifférence derisque etdenombredesujetsnéces-
sairequ’il faut traiter sontdifférentes.En prévention primaire(WestofScotland),il
estnécessairedetraiterun nombredepatients3,5 fois supérieuràceluinécessaire
en prévention secondairepouréviterun décès,dufait d’un risquedebasetroisfois
moindre.
Parcontre,lebénéfice delafibrinolyseàla phaseaiguëdel’infarctuspossède
une valeurdeNSTidentiqueàcelledela prévention primaire,carles risquesbruts

Critèresdejugementcontinus
2
4
9
debaseont lamême valeur.Il fautcependantremarquerquela périodederéférence
du risquedebase estde5semainespourISIS2 tandisqu’elle estde4,9 anspour4S.
Ainsi,malgrédes risques relatifstrèsvoisins,lebénéfice obtenu danscestrois
situationsn’estpasdu mêmeordredegrandeur,entermedepertinence clinique
(appréciéparexempleavec leNST) : lebénéfice delafibrinolyse estsupérieurà
celuidela prévention secondaire, quiest lui-mêmesupérieuràceluidelaprévention
primaire.
Pourpoursuivredanslarelativisation desbénéficeslesunspar rapportaux
autres,il peutêtrenécessairedanscertainscasderapporterleNSTàlafréquence de
lamaladiedansla population. Ils’agit alors d’uneapprochedesantépubliquequi
raisonne entermedenombrede vies(ou d’événements)épargnées surl’ensemble
dela population. Ainsi, desbénéficesa prioriminimes(entermedeNST)peuvent
déboucher surun nombred’événementsépargnés substantiel,si lafréquence dela
maladie est importante(c’est le casdel’infarctusdu myocardeparexemple).
Avec cetexemple,il apparaît quelerisquerelatifisolédeson contexte est insuf-
fisantpourapprécierl’ampleurdu bénéfice entermedepertinence cliniqueou de
santépublique.Lestroisindices:risquerelatif, différence desrisquesetNSTou
l’un d’entre eux associé aurisquedebasesontnécessaires.
Enméta-analyse,il estrarementpossibledepouvoircalculerdirectementàpar-
tirdesessaiscestroisindices.Eneffet,lesrisquesdebasesontsouventvariables
d’un essaiàl’autre.Danscesconditions,lerisquerelatifet ladifférence derisquene
peuventpasêtresimultanémentconstantsàtraverslesessais.Sic’est lerisquere-
latifquiestconstant,ladifférence derisquevavarierenfonction du risquedebase
(etvice versa).Cephénomène estconnu sousletermed’interaction arithmétique
(cf. 31.3.A).Cependant,il estnécessaire enméta-analysequelavaleurdel’effet
traitementsoit identiquepourtouslesessais,autrementunehétérogénéité apparaît.
Ainsi,cette condition nepeutêtreremplieàlafoispourunemesurerelative etune
différence derisque(saufsi lerisquedebasevarietrèspeu),ce quiconduit àl’im-
possibilitéd’estimersimultanémentcesdeux typesdemesures, directementàpartir
desessais.
Ceproblème estcontournédelafaçon suivante,issuedu conceptdemodèle
d’effet(cf.chapitre31).Laméta-analyseestutilisée pourestimerun desdeuxindices
ensebasantsurl’hétérogénéité.Leplus souvent,il s’agit d’unemesurerelative,le
risquerelatifRR parexemple.UnrisquedebaseglobalRCestensuite estimé,à
partirdesrisquesdebasesobservésdanslesessais.Apartirde cesdeux éléments,
ladifférence derisqueDRestrecalculée par:DR=RC£RR puisleNSTpar:
NST=1 /DR.

2
5
0
Interprétation cliniquedesmesuresdel’effet traitement
23.2.Critèresdejugementcontinus
L’effetstandardisé estunevaleursansdimension. Eneffet,ladifférence desmoyennes
estdivisée parunegrandeurdemêmeunité,l’écart type.Lerapport« perd » donc
l’unitéquiétait rattachéeàlagrandeurinitiale.En partie à causede ce point,tous
leseffets standardisés,mêmeissuesdemesuresdifférentes,sontcomparables.
Latransformation effectuée permetd’obtenirunenouvellevariable aléatoire
dont l’écart type estégalà1. Lesvariablesinitialesétantsupposéesdistribuées se-
lon uneloigaussienne,l’effetstandardisél’estaussi.L’effetstandardisé correspond
donc à un z-score(appelé aussivariablestandardisée).L’intérêtde cettestandardi-
sation est multiple,maiscettestandardisation permetsurtoutdeprendre encompte
desdisparitésdansleséchellesdemesuresd’un essaiàl’autre(entermedevariance
desmesures).
A)Exempleintroductif
Cettepropriété est illustrée parl’exemplesuivant.Considéronsun étudiantquise
présenteàdeux épreuves,corrigéespardeux professeursdifférents.
EpreuveNotedel’étudiantMoyenneEcart typeAmpleurd’effet
A14/20 10,8/20 5,5/20 0.58
B12/20 10,2/20 2,25/20 0.80
Sanoteobtenueàl’épreuveAlaisseprésagerqu’il estplusperformantdanscette
disciplinequedansl’autre.Cependantcesdeux notesnesontpasdirectementcom-
parables,carmêmesi lesnotesmoyennes surl’ensembledela classesontrelative-
mentsimilaires,lesécartstypede cesnotes sontdifférents.Un desdeux professeurs
utiliseuneplusgrande amplitudedenotespourdiscriminerlesélèvesquel’autre.Il
estpossiblede calculerun effetstandardiséquiprend encompte cettedifférence de
variabilitédelanotation etdonneunevaleurstandardisée comparabled’une épreuve
àl’autre.Celui-cis’obtientencalculant ladifférence entrelanotedel’étudiantet la
moyennedela classe, puisen divisantce résultatparl’écart type.
Dansnotre exemple,l’effetstandardisérattachéàl’épreuveAest inférieurà
celuidel’épreuveB.Contrairementàlapremièreimpression, laperformance de
l’étudiantdansl’épreuveAest inférieure à celledel’épreuveB.Cetteinterprétation
provientdu fait qu’il estpossible à partird’un effetstandardisédepositionnerle
rang d’un individu dans sapopulation deréférence.Nousavonsvu qu’un effetstan-
dardisé estunevariablegaussienne.Pourunevaleurdonnée de cettevariableil est
possiblede calculerquelle est laproportion desindividus(percentile)quiontune
valeurinférieure à cettevaleurderéférence.C’est laproportion deladistribution
inférieureàlavaleurderéférence quicorrespond aussiàlaprobabilitépourqu’une
variable aléatoiregaussienneprenneunevaleurinférieure à lavaleurderéférence.

Critèresdejugementcontinus
2
5
1
Lepercentile correspondantàun effetstandardisés’obtientgrâçe à unetabledeloi
gaussienne(ou avec une calculatrice statistiqueou avec un logicieldestatistique).
Fig. 23.1. — Proportion dela distribution normale(79%) correspondantà un
z-scorede0,8.
Aun effetstandardiséde0,8, correspond 79%delapopulation (figure23.1),tan-
disqu’un effetstandardiséde0,58 correspond à72%.Pourl’étudiantdel’exemple,
28%desautresétudiantsdela classeontétéplusperformantsqueluidansl’épreuve
Acontreseulement21%dansl’épreuveB.
B)Applicationàlacomparaisondedeuxtraitements
L’effetstandardisépeutêtre conçucomme étant ladifférence quiexiste entreladistri-
bution desvaleursdu critèredejugementdanslegroupe contrôle etcelledesvaleurs
danslegroupe expérimental.Parhypothèse,cesdeux distributions sontgaussiennes
etdemême écart type.Graphiquement,l’effetstandardisé est ladistance quisépare
lesdeux modesde cesdeux distributions.Lafigure23.2 illustreun effetstandardisé
de1. Lepatient moyensoustraitement(symboliséparletrait verticald’abscisse1)
alamêmevaleurdu critèredejugementquelepatientdu groupe contrôlesitué au
84epercentiledesadistribution35.C’est-à-direqu’il occupeun rang où seulement
16%des sujetsontspontanément,avant traitement, unevaleurdu critèredejuge-
mentsupérieure.Si, parexemple,le critèredejugementest lepérimètredemarche
chez despatientsartéritiques,lepatient moyenauraune amélioration de cesperfor-
mancesqui l’amèneraàun niveau où seulement16%des sujetsontspontanément
un périmètredemarchesupérieur.
35 Valeurcorrespondantàz=1dansunetabledeloigaussienne.