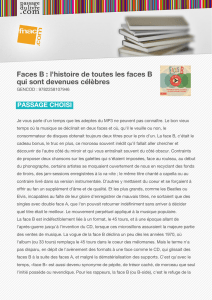
Définitions en géométrie

INTRODUCTION
Les propriétés ci-dessous sont-elles cohérentes avec les définitions "modernes" ? Si
non, donnez un contre-exemple et corrigez.
1. Le losange a 2 diagonales: la grande diagonale et la petite diagonale.
2. Le parallélogramme a deux angles obtus et deux angles aigus.
3. Dans un parallélogramme les angles opposés sont isométriques.
4. Les bases du trapèze sont les côtés non parallèles.
5. Les diagonales du parallélogramme ne sont pas isométriques.
6. Les médianes du losange sont isométriques.
7. Le rectangle a des médianes de longueurs différentes.

DÉFINITIONS EN GÉOMÉTRIE
1
ère
partie :
SURFACES

SURF.DEF.1
DÉFINITIONS EN GÉOMÉTRIE
La géométrie des Anciens (Pythagore, Euclide,…) était une géométrie statique : on
énumérait les propriétés des objets, les ressemblances, les différences,… C’est ainsi
que parmi d’autres propriétés, on citait :
pour le CARRÉ et pour le RECTANGLE
4 côtés égaux un grand côté (longueur)
un petit côté (largeur).
Au XIX
e
S, les mathématiciens ont développé une mathématique de transformations,
avec une prédilection pour les transformations continues… (on peut même parler
d’horreur des discontinuités).
Ces mathématiciens modernes ont constaté que l’on pouvait passer d’une manière
continue de l’ancien rectangle au carré et vice-versa (ce que certains expriment
par : « Le carré est un moment du rectangle »).
Pour éviter la discontinuité qui consisterait à avoir une figure qui n’est pas un
rectangle parmi une suite continue de rectangles, la définition du rectangle a été
remaniée, afin d’englober les carrés.
R R R R R C

SURF.DEF.2
RECTANGLE = TOUT QUADRILATÈRE AYANT 4 ANGLES DROITS.
De même, la définition du parallélogramme a été remaniée afin d’englober les
rectangles, et celle du trapèze de manière à englober les parallélogrammes.
TRAPÈZE = TOUT QUADRILATÈRE AYANT AU MOINS 2 CÔTÉS PARALLÈLES.
PARALLÉLOGRAMME = TOUT QUADRILATÈRE AYANT 2 PAIRES DE CÔTÉS
PARALLÈLES.
Et aussi :
LOSANGE = TOUT QUADRILATÈRE AYANT 4 CÔTÉS DE LONGUEURS ÉGALES
(OU ISOMÉTRIQUES)
Remarque : « Le rectangle a 4 angles droits » est l’énoncé d’une propriété. Ce n’est
pas l’expression d’une définition. Il suffit de penser à l’énoncé : « Le chat a 4
pattes » !
Le même souci de continuité a présidé à la définition de TRAPÈZE ISOCÈLE.
TRAPÈZE ISOCÈLES
TRAPÈZE NON ISOCÈLES
a b b’
c d e

SURF.DEF.3
En effet, on peut passer de manière continue – c’est-à-dire par une suite de trapèzes
du type a – de a à b ou à b’ mais pas de a à c, ni à d, ni à e.
Suite continue de trapèzes isocèles Les trapèzes intermédiaires ne sont
PAS isocèles.
TRAPÈZE ISOCÈLE = TOUT TRAPÈZE DONT UNE MÉDIANE AU MOINS EST
AXE DE SYMÉTRIE (ORTHOGONALE).
De même :
TRIANGLE ISOCÈLE = TOUT TRIANGLE AYANT AU MOINS 2 CÔTÉS ÉGAUX.
On passe en effet de manière continue d’un triangle ayant 2 côtés égaux à un
triangle ayant 3 côtés égaux, puis à nouveau à un triangle ayant 2 côtés égaux
(démonstration à l’aide d’un compas).