7-Exercices EM conducteur 1415

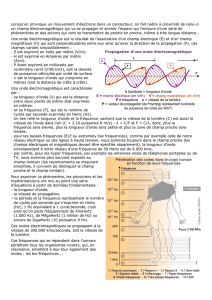
Ondes électromagnétiques au voisinage d’un conducteur
1. Une O.P.P.M. de pulsation ω se réfléchit sous incidence normale sur un plan métallique
parfaitement conducteur. Les champs E et B sont nuls dans le métal.
a. En utilisant les conditions de passage des champs E et B, déterminer les champs
réfléchis et les champs totaux ?
b. Que se passe – t – il dans le plan métallique ?
c. L’onde est polarisée circulairement, calculer le vecteur de Poynting.
2. Une plaque métallique infinie d’épaisseur e possède une conductivité électrique γ.
On envoie sur cette plaque, en incidence normale, une O.P.P.H. de pulsation ω.
a. Calculer le facteur de transmission complexe en amplitude t.
On posera δ =
γωµ
0
2
et on exprimera le résultat en fonction des paramètres
c
δω
et
δ
e
.
b. Donner une approximation de t en ne conservant que les termes du premier ordre par
rapport aux termes précédents. Calculer t, à cette approximation, lorsque
c
δω
= 2
δ
e
.
3. Entre deux plans parfaitement conducteurs, parallèles, x = 0 et x = a, se propage une
onde électromagnétique définie par son champ électrique :
E = E
0
.sin(
a
π
x).cos(ωt – k.y).u
z
.
a. L’onde vérifie – t – elle les conditions aux limites ? Donner l’équation de propagation.
b. Donner la relation de dispersion.
c. La propagation n’est possible que pour ω
c
< ω. Donner l’expression de ω
c
.
d. Donner la vitesse de phase en fonction de ω, ω
c
et c. Commenter.
4. On repère l’espace par le trièdre de référence Oxyz. Aux abscisses y = 0 et y = a, on
place deux plans métalliques parfaitement conducteurs et on étudie la propagation d’une
onde électromagnétique de pulsation ω, de vecteur d’onde k, entre ces deux plans.
L’onde se propage suivant la direction Ox.
Le vecteur champ électrique est par hypothèse de la forme : E = F(y).cos(ωt – kx).u
z
.

a. En déduire la fonction F en utilisant l’équation de propagation et les conditions aux
limites.
b. Établir la relation de dispersion.
En déduire les vitesses de phase et de groupe en fonction de ω.
Quelle est la pulsation minimale que doit avoir une onde pour se propager ?
c. Calculer le champ magnétique B et le vecteur de Poynting Π.
d. Calculer la densité d’énergie électromagnétique moyenne à l’intérieur du guide.
5. Un métal de conductivité γ, caractérisé par les constantes ε
0
et µ
0
du vide, occupe le
demi espace des x positifs. On note (u
x
, u
y
, u
z
) la base orthonormée du référentiel Oxyz.
On envoie sous incidence normale une onde électromagnétique plane de pulsation ω
dans le vide (x < 0) sur l’interface (plan x = 0) vide – métal. Le champ électrique est, sur
l’interface, E = E
0
.exp(iωt).u
y
. On négligera le courant de déplacement ε
0
t
E
∂
∂
.
a. Établir les équations différentielles vérifiées respectivement par E et par B à l’intérieur du
métal en M(x,y,z).
b. La géométrie du système impose des solutions de la forme : E(x,t) = E
1
(x).exp(iωt).u
y
.
Montrer que le champ électrique dans le métal est de la forme :
E(x,t) = E
0
.exp(–
x
δ
).cos(ωt –
x
δ
).u
y
. On exprimera δ en fonction de µ
0
, γ et ω.
En déduire, en notation réelle, le champ magnétique B.
6. Entre deux plans parfaitement conducteurs, parallèles, x = 0 et x = L, se propage une
onde électromagnétique définie par son champ électrique :
E = [E
1
.expi(ωt – k.x) + E
2
.expi(ωt + k.x)]u
z
.
a. Déterminer les relations que doit vérifier le champ E en x = 0 et en x = L.
b. En déduire k
n
et f
n
, fréquence du champ E.
c. Calculer le champ magnétique B associé à cette onde.
d. Calculer le vecteur de Poynting et sa valeur moyenne temporelle.

7. Cavité résonante
On s’intéresse à une cavité contenue entre deux plans parallèles infinis, taillée dans un
conducteur métallique parfait entre z = 0 et z = a.
On s’intéresse à un champ électromagnétique qui est la superposition de deux ondes planes
progressives monochromatiques polarisées rectilignement (selon u
x
par exemple) de sens
de propagation opposés ± u
z
.
a. Quelle est la forme du champ électrique dans la cavité ?
b. Montrer que seules certaines longueurs d’onde discrètes λ
n
peuvent exister dans la
cavité. Quelles sont les fréquences f
n
associées ?
c. Représenter sur un même graphique l’allure, à un instant donné, du champ électrique
pour les 3 plus basses fréquences.
Combien de nœuds et de ventres le mode n possède-t-il ?
8. Pression de radiation, aspect corpusculaire
D’après le principe de De Broglie, à chaque particule est associée une onde.
Pour la lumière, les particules sont des photons de masse nulle se déplaçant à la vitesse de
la lumière. Il possède une quantité de mouvement de valeur p =
h
c
ν
dirigée dans le sens de
propagation de la lumière et une énergie E = hν, h étant la constante de Planck.
a. Lors d’une réflexion de la lumière sous incidence normale sur une paroi métallique
supposée parfaite (n = – u
z
), de combien varie la quantité de mouvement (vectorielle) du
photon ?
b. Quelle est la variation de la quantité de mouvement (vectorielle) de la paroi métallique
correspondante ? On supposera le choc « idéal » et le système {photon – paroi} isolé.
c. Soit une portion de surface plane d’aire S. Quelle énergie moyenne dU provenant de
l’onde incidente vient la frapper pendant la durée dt ? En déduire le nombre moyen dN de
photons qui viennent heurter la paroi pendant la durée dt. On notera E
0
l’amplitude du
champ électrique incident.
d. Calculer la variation dp de quantité de mouvement de la surface S pendant la durée dt
due aux chocs des photons.
e. En déduire la pression de radiation due à l’onde électromagnétique.