Activité 1 - mvt circulaire satellite - PROF

1
Activité n°1 – Mouvement circulaire uniforme d’un satellite
CORRECTION
Un satellite S tourne autour de la planète Terre de
centre O avec un mouvement circulaire.
On notera :
R
T
le rayon de la Terre
 h l’altitude du satellite par rapport à la surface
de la Terre.
 M
T
la masse de la Terre et m
S
la masse du
satellite.
 G la constante de gravitation universelle.
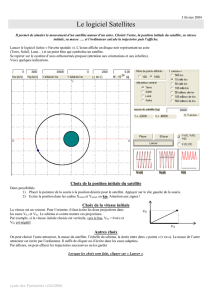
Voir schéma ci-contre.
Partie 1 – Expression de la vitesse :
1. a. Représenter sur le schéma ci-dessus la base de Frenet ayant pour origine S.
 Voir schéma
b. Rappeler les coordonnées normale (a
N
) et tangentielle (a
T
) du vecteur accélération
a
dans ce repère.
a
T
dv
a
dt
=
²
NT
v
a
R h
=
+
2. Faire l’inventaire des forces subies par le satellite.
La représenter, sans souci d’échelle, sur le schéma ci-dessus.
Seule force :
G
F
la force de gravitation.
Voir schéma
Remarque : Le satellite ne subit que la force de gravitation liée à la Terre. On néglige l’attraction du Soleil et
des autres planètes.
Le satellite n’ira pas s’écraser sur Terre car il a une vitesse qui lui permet de tourner autour de la planète…
3. Ecrire l’expression des coordonnées F
GN
et F
GT
de la force de gravitation dans la base de Frenet.
G
F
0
GT
F
=
.
( )²
T S
GN G T
M m
F F G
R h
= + = +
4. a. Ecrire la seconde loi de Newton appliquée au satellite.
.
.
S
ext G S S
dm v
d p dv
F F m m a
dt dt dt
= = = = =
∑
b. En utilisant cette loi et les coordonnées des différents vecteurs, montrer que a
T
= 0 m.s
-2
.
Comme
.
G S
F m a
=
, on peut écrire :
.
GT S T
F m a
=
.
GN S N
F m a
=
On en déduit :
Terre
T
u
N
u
S
G
F

2
0 = m
S
.a
T
donc a
T
= 0 m.s
-2
c. Que peut-on alors conclure quant à la vitesse du satellite qui tourne autour de la Terre avec un mouvement
circulaire ? (Résultat à connaître !)
T
dv
a
dt
= = 0 donc la vitesse est uniforme.
Résultat à connaître : lorsque la trajectoire d’un satellite est circulaire autour d’un astre, sa vitesse est uniforme.
(ATTENTION ! La valeur est constante mais pas le vecteur….)
5. a. En utilisant les expressions de F
GN
et a
N
, montrer que la vitesse V
S
du satellite a pour expression :
.
( )
T
ST
M
V G
R h
=
+
.
GN S N
F m a
=
On en déduit :
D’où ² .
( )
T
T
M
v G
R h
=
+
soit
.
( )
T
ST
M
V G
R h
=
+
b. Quelle est l’influence de la masse du satellite sur sa vitesse ?
Aucune, elle n’intervient pas dans l’expression de la vitesse.
c. Montrer que de l’altitude h du satellite va dépendre sa vitesse. On expliquera aussi comment évolue cette
vitesse en fonction de l’altitude.
On remarque que le seul paramètre qui peut varier dans la formule est h, M
T
, R
T
étant constants.
Comme h est au dénominateur, plus h augmente plus la vitesse diminue. Plus h est petit, plus la vitesse sera
grande.
En fonction de son altitude, le satellite ne peut pas avoir n’importe quelle vitesse !
Partie 2 – Expression de la période de révolution :
1. Donner une définition de « période de révolution ».
On notera cette période T dans la suite de l’exercice.
La période de révolution d’un satellite est la durée nécessaire pour effectuer un tour autour de l’astre.
2. Donner l’expression littérale du périmètre P du cercle décrit par le satellite en fonction de R
T
et h.
P = 2 Π (R
T
+ h)
3. En déduire l’expression de T en fonction de R
T
, h, et V
S
.
2 ( )
T
S S
R h
P
TV V
Π +
= =
4. En utilisant l’expression de V
S
, montrer que l’expression de T est :
3
( )
2.
T
T
R h
TG M
+
= Π
3
2 ( ) 2 ( ) ( )
2.
.( )
T T T
S T
T
T
R h R h R h
TV G M
M
GR h
Π + Π + +
= = = Π
+

3
5. a. Rappeler la troisième loi de Kepler.
3
²T
cte
a
= avec a le demi grand axe.
b. Que vaut le demi grand axe dans cet exercice ?
a = R
T
+ h
c. D’après l’expression de T , exprimer le rapport
3
²
( )
T
T
R h
+
3
( )
2.
T
T
R h
TG M
+
= Π donc
3
( )
² 4 ². .
T
T
R h
TG M
+
= Π soit 3
² 4 ²
( ) .
T T
T
R h G M
Π
=
+
d. Montrer que cette expression vérifie la troisième loi de Kepler. En déduire alors l’expression de la
constante et montrer qu’elle ne dépend bien que de l’astre autour duquel gravite le satellite.
3
²
( )
T
T
R h
+
est bien égale à une valeur constante dont les caractéristiques dépendent de la masse de l’astre autour
duquel le satellite tourne.
Partie 3 – Application numérique :
La Lune décrit une trajectoire quasi circulaire de rayon r = 3,84.10
5
km, autour de la Terre de masse M
T
=
6,0.10
24
kg. La constante de gravitation universelle vaut G = 6,67.10
-11
N.m².kg
-2
.
Calculer la vitesse de la Lune autour de la Terre.
24
5 3
6,0.10
. .
3,84.10 .10
T
S
M
V G G
r
= =
= 1020,9 m.s
-1
= 1,0.10
3
m.s
-1
soit 1,0 km.s
-1
soit 3,6.10
3
km/h…
Attention, r doit être en mètre (m).
Calculer la période de révolution de la Lune.
3 8 3
11 24
(3,84.10 )
2 2
. 6,67.10 6,0.10
T
r
TG M
−
= Π = Π ×
=
2363405
s soit 2,4.10
6
s.
Conversion en jours :
6
2,4.10
86400
T = = 27,7 soit 28 jours.
MBriveT – http://mbrivet.free.fr