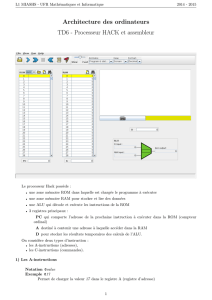
R L`essentiel - Pearson France

14
Analyse des données
Ce chapitre décrit un certain nombre de techniques pour analyser les données avec
R. La plupart des fonctions décrites ici permettent de préparer les données pour
d’autres analyses ou sont les briques de base pour d’autres analyses.
Statistiques descriptives
R propose plusieurs fonctions pour calculer les statistiques descriptives.
La fonction
mean permet d’obtenir la moyenne d’un vecteur, tandis que les fonc-
tions min et max renvoient, respectivement, la valeur minimale et maximale. À titre
d’exemple, nous utiliserons le jeu de données dow30 que nous avions créé dans la
section "Exemple plus complexe" du Chapitre 12. Ces données sont également
disponibles dans le package nutshell :
> library(nutshell)
> data(dow30)
> mean(dow30$Open)
[1] 36.24574
> min(dow30$Open)
[1] 0.99
> max(dow30$Open)
[1] 122.45
Dans chacune de ces fonctions, le paramètre na.rm précise le traitement réservé aux
valeurs NA ; par défaut, si un seul élément du vecteur vaut NA , ces fonctions renvoient NA .
Avec na.rm=TRUE , les valeurs NA sont ignorées:
> mean(c(1,2,3,4,5,NA))
[1] NA
> mean(c(1,2,3,4,5,NA),na.rm=TRUE)
[1] 3
Vous pouvez également supprimer les valeurs extrêmes lorsque vous utilisez la
fonction mean . Pour ce faire, servez-vous du paramètre trim pour préciser la fraction
des observations à ôter à chaque extrémité du vecteur.
Livre R-Essentiel.indb 291 06/10/11 18:20
© 2011 Pearson Education France – R, L'essentiel – Joseph Adler

292 Statistiques avec R Partie IV
> mean(c(-1,0:100,2000))
[1] 68.4369
323
> mean(c(-1,0:100,2000),trim=0.1)
[1] 50
Pour calculer le minimum et le maximum en une seule opération, utilisez la fonction
range , qui renvoie un vecteur contenant ces deux valeurs:
> range(dow30$Open)
[1]
0.99 122.45
La fonction quantile permet, quant à elle, de renvoyer les valeurs à différents
percentiles (indiqués par le paramètre
probs ):
> quantile(dow30$Open, probs=c(0,0.25,0.5,0.75,1.0))
0% 25% 50% 75% 100%
0.990 19.655 30.155 51.680 122.450
Ce résultat spécique (minimum, 25e percentile, médiane, 75e percentile et maximum)
peut être obtenu plus simplement, grâce à la fonction fivenum :
> fivenum(dow30$Open)
[1] 0.990 19.650 30.155 51.680 122.450
Pour obtenir l’écart interquartile (la différence entre les valeurs du 25e et du 75e
percentile), utilisez la fonction IQR :
> IQR(dow30$Open)
[1] 32.025
Chacune de ces fonctions a sa propre utilité mais peut également être utilisée avec
apply , tapply ou une autre fonction d’agrégation pour calculer les statistiques d’un
data frame ou des sous-ensembles d’un data frame.
La fonction la plus commode pour obtenir un récapitulatif s’appelle
summary . C’est
une fonction générique qui peut s’appliquer à des data frames, des matrices, des
tables, des facteurs et d’autres objets. Voici, par exemple, ce qu’elle produit lorsqu’on
l’applique au jeu de données dow30 :
> summary(dow30)
symbol Date Open High
MMM : 252 2008-09-22: 30 Min. : 0.99 Min. : 1.01
AA : 252 2008-09-23: 30 1st Qu.: 19.66 1st Qu.: 20.19
AXP : 252 2008-09-24: 30 Median : 30.16 Median : 30.75
T : 252 2008-09-25: 30 Mean : 36.25 Mean : 36.93
BAC : 252 2008-09-26: 30 3rd Qu.: 51.68 3rd Qu.: 52.45
BA : 252 2008-09-29: 30 Max. :122.45 Max. :122.88
(Other):5970 (Other) :7302
Low Close Volume Adj.Close
Min. : 0.27 Min. : 0.75 Min. :1.336e+06 Min. : 0.75
Livre R-Essentiel.indb 292 06/10/11 18:20
© 2011 Pearson Education France – R, L'essentiel – Joseph Adler

Analyse des données 293
Chapitre 14
1st Qu.: 19.15 1st Qu.: 19.65 1st Qu.:1.111e+07 1st Qu.: 19.38
Median : 29.55 Median : 30.10 Median :1.822e+07 Median : 29.41
Mean : 35.53 Mean : 36.24 Mean :5.226e+07 Mean : 35.64
3rd Qu.: 50.84 3rd Qu.: 51.58 3rd Qu.:4.255e+07 3rd Qu.: 50.97
Max. :121.62 Max. :122.11 Max. :2.672e+09 Max. :122.11
Comme vous pouvez le constater, summary donne des informations sur chaque
variable du data frame. Pour les valeurs numériques, elle montre les valeurs mini-
male, du 1er quartile, de la médiane, de la moyenne, du 3e quartile et maximale.
Pour les facteurs, elle afche le nombre des valeurs les plus fréquentes (les moins
fréquentes sont regroupées dans la catégorie " Other "). Elle ne produit rien d’utile
pour les valeurs caractères.
La fonction
stem est un outil commode pour examiner en mode texte la distribution
d’un vecteur numérique:
stem(x, scale = 1, width = 80, atom = 1e-08)
Le paramètre x est le vecteur concerné, scale contrôle la longueur du tracé, width ,
sa largeur et atom est un facteur de tolérance.
Examinons par exemple les tentatives de transformation pendant la saison 2005 de
la NFL. Plus précisément, nous voulons étudier les distances des tentatives pour les
transformations ratées. Nous utiliserons donc la fonction
subset pour ne sélection-
ner que les transformations ratées, puis nous afcherons les distances (en yards) des
tentatives qui leur correspondent:
> stem(subset(field.goals, play.type=="FG no")$yards)
The decimal point is at the |
20 | 0
22 |
24 |
26 | 00
28 | 0000000
30 | 0000000
32 | 00000000
34 | 000
36 | 0000
38 | 00000000000000
40 | 0000000000
42 | 0000000000000000
44 | 000000000000
46 | 000000000000000000
48 | 000000000000000000
50 | 000000000000
52 | 0000000000000000000
54 | 0000
56 | 000
58 | 00
60 | 00
62 | 0
Livre R-Essentiel.indb 293 06/10/11 18:20
© 2011 Pearson Education France – R, L'essentiel – Joseph Adler

294 Statistiques avec R Partie IV
Corrélation et covariance
Lorsque l’on analyse des données, il est très fréquent de vouloir savoir si deux
variables sont corrélées. Informellement, la corrélation répond à la question "si
j’augmente (ou diminue) x, est-ce que y augmentera (ou diminuera), et de com-
bien ?". Formellement, elle mesure la dépendance linéaire de deux variables
quelconques. Ses valeurs varient de –1 à 1; 1 signie que l’une des variables
est une fonction linéaire positive de l’autre, 0, que les deux variables ne sont pas
corrélées du tout et -1, que l’une des variables est une fonction linéaire négative
de l’autre (les deux progressent dans des directions totalement opposées; voir
Figure14.1).
Figure 14.1
Corrélation.
La mesure de corrélation la plus utilisée est le coefcient de corrélation de Pearson
(c’est la formule qui se cache derrière la fonction CORREL d’Excel):
r=i
ni i
i
nii ni
x x y y
x x y y
=
= =
Â
 Â
1
1212
( – )( – )
( – ) ( – )
où _ x est la moyenne de x et _ y la moyenne de y . La corrélation de Pearson fonctionne
mieux avec des données qui suivent une distribution normale. Une autre fonction de
corrélation est le coefcient de corrélation de Spearman, qui est non paramétrique
car il ne fait aucune supposition sur la distribution sous-jacente:
r =n x y x y
n x x n y y
i i i i
iii
( – )–( )( )
( )–( ) ( )–(
ÂÂÂ
ÂÂ 2 2 2 ii )2
ÂÂ
Le tau de Kendall, quant à lui, permet d’exprimer la relation entre deux variables
quelconques. Sa formule fonctionne en comparant les rangs des valeurs dans les
deux variables, pas en comparant ces variables elles-mêmes:
t =
n n
n n
c d
–
/ ( – )1 2 1
Livre R-Essentiel.indb 294 06/10/11 18:20
© 2011 Pearson Education France – R, L'essentiel – Joseph Adler

Analyse des données 295
Chapitre 14
Dans cette formule, n est la longueur des deux variables, nc , le nombre de paires
concordantes et nd , le nombre de paires discordantes. Pour calculer les corrélations
avec R, vous disposez de la fonction cor , qui permet d’effectuer chacune de ces
mesures de corrélation que nous venons d’évoquer:
cor(x, y = NULL, use = "everything",
method = c("pearson", "kendall", "spearman"))
Vous pouvez calculer les corrélations entre deux vecteurs (désignés par x et y ),
sur un data frame ou sur une matrice; dans ces deux cas, y=NULL et cor calcule-
ront la corrélation entre chaque paire de variables pour renvoyer une matrice des
résultats.
Le paramètre
method précise la formule utilisée pour calculer la corrélation et use
indique comment traiter les valeurs
NA : si vous voulez que la fonction déclenche
une erreur en présence de valeurs NA , utilisez use="all.obs" ; si vous voulez qu’elle
renvoie
NA si l’un des éléments est NA , choisissez use="everything" ; pour ne pas
tenir compte des valeurs NA , choisissez use="complete.obs"  ; pour ne pas tenir
compte des valeurs NA mais renvoyer NA si tous les éléments valent NA , utilisez
use="na.or.complete" ; enn, pour ne pas tenir compte des paires dont au moins
une des valeurs est NA , choisissez use="pairwise.complete.obs" .
Examinons les données sur les naissances de 2006 que nous avions déjà utilisées
auparavant. Plus précisément, nous voulons savoir si la prise de poids de la mère
a un lien avec le poids du bébé. Commençons par ne sélectionner que les poids de
naissance et les prises de poids corrects. Nous exclurons également les naissances
prématurées (j’ai exclu les termes de moins de 35semaines bien que, technique-
ment, ce ne soient pas nécessairement des prématurés). Enn, nous ne gardons que
les naissances d’enfants uniques:
> births2006.cln <- births2006.smpl[
+ !is.na(births2006.smpl$WTGAIN) &
+ !is.na(births2006.smpl$DBWT) &
+ births2006.smpl$DPLURAL=="1 Single" &
+ births2006.smpl$ESTGEST>35,]
Examinons d’abord la relation entre ces deux variables. Comme il y a 3 232 884
observations, un nuage de points normal serait trop difcile à lire. C’est la raison
pour laquelle nous préférons utiliser smoothScatter :
> smoothScatter(births2006.cln$WTGAIN,births2006.cln$DBWT)
Le diagramme obtenu est celui de la Figure 14.2. En l’étudiant, nous pouvons nous
attendre à constater une légère corrélation (nous n’en attendons pas une très forte à
cause de la forte concentration au centre, mais celle-ci est peu inclinée). Calculons
la corrélation de Pearson:
> cor(births2006.cln$WTGAIN,births2006.cln$DBWT)
[1] 0.1750655
Livre R-Essentiel.indb 295 06/10/11 18:20
© 2011 Pearson Education France – R, L'essentiel – Joseph Adler