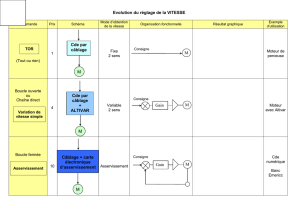
Analyse de la stabilité

Exercice 1 : Etude de la stabilité d’un asservissement de position angulaire
Le mouvement de rotation de l’arbre d’un moteur à courant continu de type à excitation indépendante résulte de
l’action du champ magnétique produit par le circuit inducteur, sur le circuit de l’induit. La variation du couple
moteur appliqué sur l’arbre peut s’obtenir par la variation du champ magnétique et donc du courant inducteur
tout en maintenant le courant induit constant (commande par l’inducteur).
L’objectif est d’asservir la position angulaire à une tension de référence et d’analyser ensuite les performances
en stabilité en considérant les deux schémas de commande :
 Commande sans retour tachymétrique
 Commande avec retour tachymétrique
On admet les fonctions de transfert suivantes :
m
1
1 2
m
2
1 2
K
(p)
G (p) V(p) p(1 T p)((1 T p)
K
(p)
G (p) V(p) (1 T p)((1 T p)
θ
= =
+ +
Ω
= =
+ +
K
m
désigne le gain en vitesse, T
1
la constante de temps électrique et T
2
la constante de temps mécanique. θ et Ω
désignent respectivement la position et la vitesse angulaire du moteur.
Dans la suite on traitera le problème avec les valeurs numériques suivantes :
K
m
=1 volt.rd/s T
1
= 0.1 s T
2
= 0.5 s
On désire que la position angulaire suit un signal de référence représenté par une tension V
e
Pour cela on
considère une boucle d’asservissement comportant :
 un générateur de tension V
e
.
 un amplificateur de tension de gain K ajustable et supposé indépendant de la fréquence dans la bande
d’utilisation.
 un comparateur de tensions.
 un organe potentiométrique fournissant une tension proportionnelle à la position angulaire; soit V
s
= K
θ
.θ, K
θ
= 4 volt/rd.
Dans une première étape l’asservissement de position est considéré sans retour tachymétrique et dans une
deuxième étape on ajoutera un retour tachymétrique. Cette opération consiste à monter sur l’arbre du moteur,
une génératrice tachymétrique (GT) qui permet de délivrer une tension V
g
proportionnelle à la vitesse de
rotation; soit V
g
= 0.25 Ω.
1. Compléter le schéma fonctionnel de l’asservissement :
I
θ
,
Ω
L
R
V
Induit à courant
constant
Inducteur
Charge

2. Etablir la fonction de transfert en boucle ouverte dans les deux cas: interrupteur ouvert (Asservissement sans
retour tachymétrique) et interrupteur fermé (Asservissement avec retour tachymétrique).
3. Etude du système asservi sans retour tachymétrique
a) Etudier la stabilité de l’asservissement en fonction de K par une méthode de votre choix.
b) Déterminer le gain K
1
pour avoir une marge de gain de 10 db. En déduire la marge de phase.
c) Déterminer le gain K
2
pour avoir une marge de phase de 45°. En déduire la marge de gain.
4. Etude du système asservi avec retour tachymétrique
a) Quelle est la valeur limite de K correspondant à la stabilité de la boucle ? La comparer à la valeur trouvée en
3a.
b) Que deviennent les marges de gain et de phase pour les valeurs de K
1
et K
2
trouvées précédemment ?
c) Conclure sur l’intérêt de l’insertion d’une génératrice tachymétrique dans un asservissement de position.
5. Analyse statique et transitoire
a) Calculer le gain statique entre Vs et Ve dans les deux cas de schéma de commande. Interprétation.
b) Par analyse qualitative, indiquer l’allure de la réponse indicielle pour les différentes valeurs de K calculées.
Parmi toutes les valeurs de K, préciser pour laquelle le dépassement indiciel sera le plus faible.
Exercice 2 : Analyse de la stabilité d’une boucle de régulation de niveau
La figure ci-dessous représente le schéma de principe de l'asservissement et de la régulation de niveau
d'eau dans un réservoir. On désire que celui-ci puisse suivre un niveau de consigne h
c
affichable par un
potentiomètre P
e
même en présence de variation du débit d'utilisation Q
u
.
Pour cela, on propose un schéma de commande qui consiste d'appliquer une tension d'erreur V
c
-V
h
, amplifiée
par un amplificateur comparateur de gain K
1
, à un asservissement de position de la vanne. Cet asservissement
comporte un amplificateur de gain K
2
qui alimente un moteur à courant continu et à excitation indépendante et
constante. En tournant, le moteur entraîne la tige de la vanne par l'intermédiaire d'un réducteur; ce qui permet
l'ajustement d'un débit d'entrée Qe.
On donne les caractéristiques suivantes :
 Réservoir : section de base S= 0.5m
2
; h
max
= 1 m.
 Potentiomètre de consigne Pe : gradué de 0 à h
max
. La tension de sortie est proportionnelle au niveau de
consigne ; soit Vc=K
c
h
c
avec K
c
= 20 v/m.
 Moteur à cc : la fonction de transfert ( )
(1 )
m
m
K
M p
p T p
=+ avec K
m
= 0.5 rd/s/v et T
m
=0.1 s
 Potentiomètre de sortie Ps
;
capte la position angulaire et fournie une tension qui lui est proportionnelle; soit
V
m
=K
p
θ
m
avec K
p
= 1 v/rd.
 Réducteur : le rapport de réduction
1
20
r
rm
θ
θ
= =
Vanne : permet de fournir un débit q proportionnel à la positon angulaire réduite; soit Q = K
v
θ
r
avec
K
r
=0.1 m
3
/s/rd.
capteur de niveau : permet de fournir une tension V
h
proportionnelle au niveau h ; soit V
h
=K
c
h.
1. Etablir le schéma fonctionnel de l’installation.
2. Calculer la fonction de transfert en boucle fermée relative à la boucle d’asservissement de position (boucle
interne).
3. Fixer une valeur de K
2
de manière à ce que cette boucle ne présente pas de dépassement transitoire.
+
+
-
Interrupteur
manuel
GT
Ω
ϑ
-
Ve

4. On étudie la stabilité de la boucle externe (asservissement de niveau). Etablir la condition de stabilité du
système en fonction de K
1
par une méthode de votre choix.
5. Déterminer la valeur de K
1
qui permet d’assurer une marge de gain de 15dB.
6. Déterminer la valeur de K
1
qui permet d’assurer une marge de phase de 45°.
7. En réalité, la fonction de transfert des comparateurs amplificateurs (de conception identique) possède une constante de
temps Te = 0.05s qui a été négligée dans les précédents calculs. On demande :
- D’évaluer l’impact de cette approximation en calculant la valeur de K
1
correspondant à la limite de stabilité. (La valeur de
K
2
est celle proposée en 3) ;
- D’évaluer les nouvelles marges de stabilité en adoptant les valeurs de K
1
trouvées en 5 et 6.
Exercice 3 : Stabilité dans le plan de Bode et Black
Les courbes données par les figures ci-dessous correspondent à la réponse en fréquence en boucle ouverte
KG(p) obtenues pour K=1 d’un système asservi à retour unitaire :
Etude dans le plan de Bode
1. Justifier que la fonction de transfert G(p) ne possède pas d’intégration.
2. Quel est le gain statique du système représenté par G(p)?
3. Quel est l’ordre de G(p) ?
4. Pour K= 1, le système asservi est-il stable?
5. Quelle est la valeur de K qui correspond à la limite de stabilité ?
6. Quelle est la valeur de K qui permet d’assurer une marge de gain de 10db ?. En déduire dans ce cas la marge
de phase.
7. Quelle est la valeur de K qui permet d’assurer une marge de phase de 40° ?. En déduire dans ce cas la marge
de gain.
Etude dans le plan de Black
Retrouver l’ensemble des résultats obtenus en utilisant la représentation dans le plan de Black.
+
- K G(p)
e
Moteur
θ
θθ
θ
m
θ
θθ
θ
r
Alimentation
Vanne
-
K
2
+
Potentiomètre
Ps
h
c
V
c
V
h
Q
e
Q
u
h
max
h
Capteur
de niveau
Potentiomètre
Pe
-
K
1
+

Courbes dans le plan de Black
Exercice 4 : Régulation de débit massique
La figure ci-dessous représente une boucle de régulation de débit massique. L’objectif par conséquent est de
disposer d’un débit constant malgré les fluctuations qui peuvent affectées ce processus.

Le schéma fonctionnel est donné par la figure suivante :
On admet les fonctions de transfert suivantes :
-p
R(p) = k > 0
e
H(p)=
1+3p
On propose d’étudier la stabilité de la boucle en fonction du gain k du régulateur.
1. Tracer dans le plan de Nyquit le lieu de transfert en boucle ouverte T(p) = R(p)H(p).
2. Justifier que le système bouclé est conditionnellement stable.
3. Donner la valeur limite de k au-delà de laquelle le système bouclé devient instable.
4. Régler la valeur de k de manière à avoir une marge de gain de 10db.
5. La méthode algébrique de Routh n’est pas applicable à cause du terme de retard e
-p
. Néanmoins, en faisant une
approximation de celui-ci, retrouver approximativement la valeur de k établie en 3. Comment peut-on améliorer
cette démarche ?
y
x
Vanne
I/P
FY FC
FT
Consigne w
- FT : Transmetteur
de débit
- FC : Régulateur de
débit
- FY : Module de
conversion courant -
pression
y
+
-
R(p) H(p)
x
w