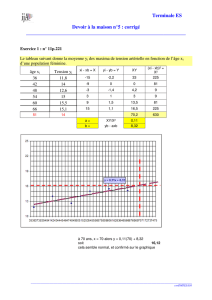
fonction reciproque d`une fonction continue, d`une

Fonction réciproque d'une fonction continue, d'une fonction dérivable
© S. DUCHET - www.epsilon2000.fr.st 1/10
FONCTION RECIPROQUE D'UNE FONCTION CONTINUE,
D'UNE FONCTION DERIVABLE. EXEMPLES. ON SE LIMITERA
AUX FONCTIONS NUMERIQUES DEFINIES SUR UN
INTERVALLE DE R
Notations
Soit I un intervalle de R. Soit f une fonction définie sur I, à valeurs dans R. Notons f
C la courbe
représentative de f dans un repère du plan.
1) Condition d'existence d'une fonction réciproque
théorème
Si f est strictement monotone sur I, alors f réalise une bijection de I sur f(I).
démonstration
• f est bien entendu surjective de I sur f(I) ;
• Supposons f strictement croissante sur I.
Soient Iba ∈, , avec ba ≠.
ou bien ba <et on a )()( bfaf < (f étant strictement croissante sur I)
ou bien ba >et on a )()( bfaf > (f étant strictement croissante sur I)
donc )()( bfaf ≠.
• Supposons f strictement décroissante
Soient Iba ∈, , avec ba ≠.
ou bien ba <et on a )()( bfaf > (f étant strictement décroissante sur I)
ou bien ba >et on a )()( bfaf < (f étant strictement décroissante sur I)
donc )()( bfaf ≠.
Dans tous les cas, si ba ≠ alors )()( bfaf ≠donc f est injective de I sur f(I).
définition (fonction réciproque)
Soit f une fonction bijective de I sur J, où J est un intervalle de R. On appelle fonction réciproque de
f l'application notée 1− f définie sur J par xyf =
−)( 1, où x est l'unique élément de I tel que
yxf =)(.
On note ),,( 211 eeOR =un repère du plan.
propriété géométrique
Soit f une fonction bijective de I sur J. Soit 1− f la fonction réciproque de f. Notons f C et 1−
f
C les
courbes représentatives des fonctions f et 1−
fdans 1
R. Alors
(
)
f
fCsC
=
−1, où s est la symétrie par
rapport à la droite
(
)
21 eeRO ++ , parallèlement à
(
)
21 eeRO −+ .

Fonction réciproque d'une fonction continue, d'une fonction dérivable
© S. DUCHET - www.epsilon2000.fr.st 2/10
démonstration
Déterminons d'abord l'expression analytique de s :
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=−+ 10
01
),;( 2121 eeeesmat .
Soit P la matrice de passage de la base ),( 21 eee = à la base ),(' 2121 eeeee −+= .
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=11
11
P.
1
10
01
);( −
×
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
×= PPesmat
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=11
11
10
01
11
11
2
1
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=01
10
Les coordonnées des points seront exprimées dans le repère 1
R.
Soit f
CyxM ∈);(. On a )(xfy = donc xyf =
−)( 1.
Soit )(' MsM =. M' a donc pour coordonnées );( xy . xyf =
−)( 1 donc 1
'− ∈f CM . Par conséquent,
(
)
1−
⊂f
fCCs .
On montre de la même façon que
(
)
f
fCCs ⊂
−1 . s étant involutive, on a donc
(
)
f
fCsC ⊂
−1.
Donc
(
)
f
fCsC =
−1.
2) Fonctions réciproques et continuité
théorème des valeurs intermédiaires
Si f est continue sur un intervalle I, alors )(If est un intervalle de R.
démonstration
Soient )(, If∈βα , avec β<
α
.Montrons que )(],[ If⊂
β
α
. Soit ],[
β
α
∈
t. Soient Ixx
∈
21, tels
que )( 1
xf=α et )( 2 xf=β . Soit la fonction définie par txfx
−
=
φ
)()( . Nous allons montrer qu'il
existe Ix ∈
0 tel que txf =)( 0, c'est-à-dire 0)( 0
=
φ
x.
Si α=t, alors 10 xx =. Si β=t, alors 20 xx
=
. On suppose donc désormais que
{}
βα∉ ,t.
On a 0)( 1<−α=φ tx et 0)( 2>−β=
φ
tx .
Soient )(n
aet )(n bles suites définies par :
• 10 xa = et 20 xb = ;
• Pour tout entier naturel n :
Si 0
2≥
⎟
⎠
⎞
⎜
⎝
⎛+
φnn ba , on pose nn aa =
+1et 2 1nn nba
b
+
=
+.
Si 0
2<
⎟
⎠
⎞
⎜
⎝
⎛+
φnn ba , on pose 2
1nn nba
a+ =
+ et nn bb
=
+1.

Fonction réciproque d'une fonction continue, d'une fonction dérivable
© S. DUCHET - www.epsilon2000.fr.st 3/10
On a : 2
,11 nn
nn ba
baNn − =−∈∀ ++ .
Par une récurrence immédiate, on a : n
nn ba
baNn 2 ,00 − =−∈∀ .
Montrons par récurrence que : nnnn bbaaNn
≤
≤
≤
∈∀ ++ 11 ,.
Soit P(n) la propriété suivante : nnnn bbaa
≤
≤
≤++ 11 .
• 0=n :
Si 0
200 ≥
⎟
⎠
⎞
⎜
⎝
⎛+
φba , alors 01 aa = et 200
1ba
b
+
=.
0110
0
00
1
0
00
1
2
2bbaa
a
aa
b
b
bb
b
≤≤=⇒
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
+
≥
=
+
≤.
Si 0
200 <
⎟
⎠
⎞
⎜
⎝
⎛+
φba , alors 200
1ba
a+ = et 01 bb
=
.
1010
0
00
1
10
00
1
2
2bbaa
a
aa
a
bb
bb
a
=≤≤⇒
⎪
⎪
⎭
⎪
⎪
⎬
⎫
=
+
≥
==
+
≤.
• Soit n un entier naturel. Supposons P(n) vraie.
On montre que P(n+1) est vraie comme précédemment, en distinguant les cas.
• Donc P(n) est vraie pour tout entier naturel n.
)( n
a est donc une suite croissante, )(n bune suite décroissante et 0
⎯
⎯
⎯
→
⎯
−
∞⎯→⎯n
nn ba . Ces deux
suites sont donc adjacentes. Soit l leur limite commune.
Par construction, on a : 21
,xbaxNn nn
≤
≤
≤∈∀ donc ],[ 21 xxl
∈
.
φétant continue sur I donc en l, on a )()( la n
n
φ
⎯
⎯
⎯
→
⎯
φ∞⎯→⎯ et )()( lb n
nφ
⎯
⎯
⎯
→
⎯
φ
∞⎯→⎯.
Par construction, 0)()( ≤φφ nn ba pour tout entier n donc 0)( 2≤φ ldonc 0)(
=
φ
l, avec Il∈.
On a donc tlf =)(.
théorème
Si f est continue et strictement monotone sur I, alors 1− f est continue, strictement monotone et de
même sens de monotonie que f.
démonstration
Monotonie :
Soit 1−
=fg .
Soient )(', Ifyy ∈ tels que 'yy <.
)'(')(,', xfyetxfyIxx ==∈∃ . On a donc )(ygx
=
et )'(' ygx
=
. 'xx
≠
car g est injective.
• si f est strictement croissante sur I, alors 'xx
<
. Donc )'()( ygyg
<
et g est strictement
croissante sur )(If ;

Fonction réciproque d'une fonction continue, d'une fonction dérivable
© S. DUCHET - www.epsilon2000.fr.st 4/10
• si f est strictement décroissante sur I, alors xx
<
'. Donc )()'( ygyg
<
et g est strictement
décroissante sur )(If .
g est donc strictement monotone sur )(If de même sens de monotonie que f.
Continuité
Soit )(
0Ify ∈. )(, 000 xfyIx =∈∃ . On suppose f strictement croissante sur I.
1er cas : 0
0Ix ∈
Soit 0>ε ? Ixx ⊂
ε
+ε−ε<ε>ε∃ ]','[,',0' 00 .
)()'( 0Ifxf ∈ε− et )()'( 0Ifxf ∈ε
+
.
Soient )'( 001 ε−−=η xfy et 002 )'( yxf
−
ε
+
=η .
Soit ),min( 21 ηη=η
Soit [,])( 00 η
+
η−∩∈ yyIfy . On a :
η+<<η− 00 yyy
donc 2010 η+<<η− yyy
donc )'()'( 00 ε+<<ε− xfyxf .
f étant strictement croissante sur I, g est strictement croissante sur f(I)
donc )'()()'( 00 ε+<<ε− xfgygxfg DD
donc ')(' 00
ε
+<<ε− xygx
donc ')()( 0ε<− ygyg
Donc : ε<−⇒η<−∈∀>η∃>ε∀ )()(),(,0,0 00 ygygyyIfy .
g est donc continue en 0
y.
2ème cas : o
IIx −∈
0
Même démonstration que précédemment en considérant ]';[ 00
ε
+
xx ou ];'[ 00 xx ε
−
Remarque : On n'utilise pas la continuité de f dans cette démonstration. La stricte monotonie de f et
le fait que f est définie sur un intervalle suffisent pour obtenir la stricte monotonie et la continuité de
g.
théorème
Les assertions suivantes sont équivalentes :
(i) f est continue et injective sur I ;
(ii) f est continue et strictement monotone sur I ;
(iii) f est strictement monotone sur i et f(I) est un intervalle.
démonstration
)()( iii ⇒
On suppose que f est continue et injective sur I. Montrons que f est strictement monotone sur I.
baIba ≠∈ ,, . f étant injective, on a )()( bfaf
≠
. Supposons )()( bfaf
<
(si )()( bfaf >, on
s'intéresse à la fonction –f). Montrons qu'alors f est strictement croissante sur I.
Soit Ix∈.

Fonction réciproque d'une fonction continue, d'une fonction dérivable
© S. DUCHET - www.epsilon2000.fr.st 5/10
• cas où bxa << : montrons que )()()( bfxfaf
<
<
.
Supposons )()( afxf <. Alors )()()( bfafxf
<
<. f étant continue sur ],[ bx ,
()
];[ bxf est un
intervalle contenant )(xf et )(bf donc
(
)
],[)](),([ bxfbfxf ⊂ donc
()
],[)( bxfaf
∈
.
Donc )()( xfaf <. De même, on montre que )()( bfxf
<
• cas où bax << : on montre comme précédemment que )()()( bfafxf <
<
• cas où xba << : on montre comme précédemment que )()()( xfbfaf <
<
Soient maintenant Ixx ∈', tels que 'xx <. Il suffit d'étudier tous les cas :
'
'
'
'
'
'
xxba
xbxa
bxxa
xbax
bxax
baxx
<<<
<<<
<<<
<<<
<<<
<<<
et d'utiliser ce qui précède pour montrer que l'on a toujours )'()( xfxf
<
)()( iiiii ⇒
C'est le théorème des valeurs intermédiaires qui donne le résultat.
)()( iiii ⇒
f étant strictement monotone, elle est injective.
Supposons que )(IfJ = est un intervalle de R. Quitte à travailler avec –f, on peut supposer f
strictement croissante sur I. D'après le théorème de la limite monotone, on sait que pour tout o
It∈, f
admet une limite finie à gauche en t notée )(−
tf et une limite finie à droite en t, notée )(+ tf .
Soit It∈.
• si It inf≠, )()( tftf ≤
−
• si It sup≠, )()( + ≤tftf .
Supposons que f ne soit pas continue sur I.
Il existe It∈ tel que
(
)
)()(inf tftfetIt <≠ − ou
(
)
)()(sup + <≠ tftfetIt . Plaçons-nous dans le
cas où
(
)
)()(inf tftfetIt <≠ −.
It inf≠ donc il existe It
∈
'tel que tt <'.
)(If est un intervalle de R contenant )'(tf et )(tf donc )()](),'([ Iftftf ⊂.
Donc )()](),([ Iftftf ⊂
−car )()()'( tftftf <≤ −.
Soit )[(),(] tftfy −
∈. Alors )[(),'(] tftfy∈. )(If étant un intervalle, il existe Ix∈ tel que
)(xfy =.
Si t
x
≥, alors )()( tfxf ≥(f étant croissante) : contredit le fait que )[(),'(] tftfy
∈
.
Si t
x
<, alors )()( − <tfxf (f étant croissante) : contredit le fait que )[(),(] tftfy − ∈.
Dans les deux cas, il y a une contradiction.
f est donc continue sur I.