Texte du T - Math

Texte du T.P en sciences.
Partie expérimentale.
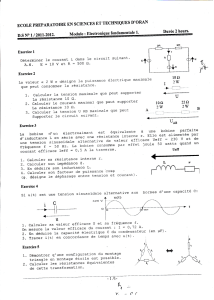
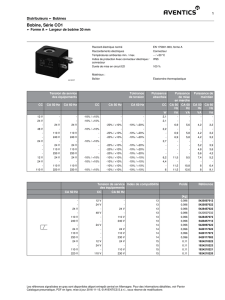
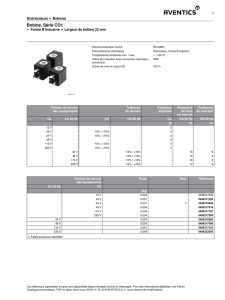
On utilise une bobine d’inductance 100 mH  10 % et de résistance interne 349 .
La formule reliant l’inductance, l’impédance, la résistance interne et la pulsation est :
22
)( rLZ 
1. Détermination de la résistance interne de la bobine.
Mesurer la résistance r de la bobine déconnectée du circuit, avec le multimètre en position ohmmètre et
mettre votre valeur dans le tableau ci-dessous.
2. Détermination de l’impédance Z de la bobine.
 Réaliser le montage suivant :
Régler le niveau du générateur basse fréquence de telle sorte que le voltmètre affiche environ 5,00 V
 Relever la tension efficace Ueff et l’intensité efficace Ieff.
 Consigner vos valeurs dans le tableau ci-dessous.
Recommencer pour les cinq autres bobines.
3. Tableau de valeurs.
 Calculer 
 Calculer l’impédance Z de la bobine.
 En déduire la valeur de l’inductance L connaissant Z, r et 
Bobine n°
1
2
3
4
5
6
r (en )
349
349
351
348
349
349
Ueff (en V)
5,00
4,95
5,06
5,03
4,98
4,96
Ieff (en mA)
14,00
13,95
14,20
14,18
13,98
14,00
Z (en )
357
355
356
355
356
354
L (en mH)
121
102
98
109
114
97

Partie mathématique
Les élèves ont déjà les notions nécessaires de statistique depuis le B.E.P.. Ils viennent juste de finir la partie
du cours concernant la loi normale centrée réduite et le calcul de probabilité en utilisant la table numérique de la
fonction de répartition de la loi normale.
Texte de l’activité.
1. Partie statistique
 Regrouper les valeurs obtenues en classes dans le tableau ci-contre.
 Compléter le tableau
 Construire l’histogramme des effectifs.
 Calculer la moyenne m et l’écart type  de ces valeurs.
 Tracer le polygone des effectifs cumulés croissants.
 Déterminer le pourcentage de bobines ayant pour valeur, une valeur inférieure de 10% à la valeur théorique.
 Déterminer le pourcentage de bobines ayant pour valeur, une valeur supérieure de 20% à la valeur théorique.
 Déterminer le pourcentage de bobines ayant pour valeur, une valeur de ± 5 % par rapport à la valeur
théorique.
Classe
Effectif
Effectif
cumulé
croissant
[75 ; 80[
1
1
[80 ; 85[
2
3
[85 ; 90[
4
7
[90 ; 95[
7
14
[95 ; 100[
13
27
[100 ; 105[
19
46
[105 ; 110[
14
60
[110 ; 115[
8
68
[115 ; 120[
2
70
[120 ; 125[
2
72
2. Partie probabilité.
 Par quelle courbe peut-on ajuster l’histogramme ?
On considère que la distribution des mesures suit une loi normale N (m ; ).
Dans ces conditions, la variable
mX
T
est la variable normale centrée réduite.
A l’aide de la table numérique de la fonction de répartition de la loi normale :
 Déterminer la probabilité qu’une bobine ait pour valeur, une valeur inférieure de 10% à la valeur théorique.
 Déterminer la probabilité qu’une bobine ait pour valeur, une valeur supérieure de 20% à la valeur théorique.
 Déterminer la probabilité qu’une bobine ait pour valeur, une valeur de ± 5 % par rapport à la valeur
théorique.
Comparer les résultats de la partie probabilité avec ceux de la partie statistique.
Remarque : les élèves déterminent ensemble l’amplitude des classes.