Fiche démonstration Pythagore 4e

Fiche démonstration Pythagore 4e
(1) (2)
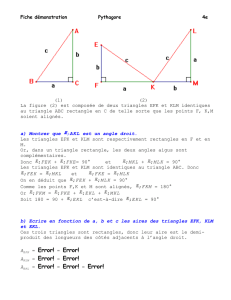
La figure (2) est composée de deux triangles EFK et KLM identiques
au triangle ABC rectangle en C de telle sorte que les points F, K,M
soient alignés.
a) Montrer que Æ;AKL est un angle droit.
Les triangles EFK et KLM sont respectivement rectangles en F et en
M.
Or, dans un triangle rectangle, les deux angles aigus sont
complémentaires.
Donc Æ;FEK + Æ;FKE= 90° et Æ;MKL + Æ;MLK = 90°
Les triangles EFK et KLM sont identiques au triangle ABC. Donc
Æ;FEK = Æ;MKL et Æ;FKE = Æ;MLK
On en déduit que Æ;FEK + Æ;MLK = 90°
Comme les points F,K et M sont alignés, Æ;FKM = 180°
Or Æ;FKM = Æ;FKE + Æ;EKL + Æ;MKL
Soit 180 = 90 + Æ;EKL c’est-à-dire Æ;EKL = 90°
b) Ecrire en fonction de a, b et c les aires des triangles EFK, KLM
et EKL.
Ces trois triangles sont rectangles, donc leur aire est le demi-
produit des longueurs des côtés adjacents à l’angle droit.
AEFK =
Error!
=
Error!
AKLM =
Error!
=
Error!
AEKL =
Error!
=
Error!
=
Error!

c)Démontrer que le quadrilatère EFML est un trapèze
Le triangle EFK est rectangle en F : (EF) ┴ (FK)
Le triangle KLM est rectangle en M : (KM) ┴ (ML)
Les points F,K,M sont alignés : (FK) = (KM)
Si deux droites sont perpendiculaires à une même troisième, alors
elles sont parallèles entre elles.
Donc (EF) // (ML).
Le quadrilatère EFML a deux côtés opposés parallèles, donc c’est un
trapèze.
d) Calculer l’aire de EFML de deux façons
1ère façon : formule de l’aire du trapèze :
Error!
soit ici :
Error!
=
Error!
=
Error!
2ème façon : somme des aires des trois triangles :
AEFK + AKLM + AEKL =
Error!
+
Error!
+
Error!
=
Error!
+
Error!
e) Conclure
On a calculé l’aire du trapèze de deux façons, on peut égaliser les
deux expressions ainsi obtenues :
Error!
=
Error!
+
Error!
ñ
Error!
=
Error!
+
Error!
ñ a2+2ab+b2=2ab+c2
ñ a2+b2=c2
La relation du théorème de Pythagore est ainsi démontrée.