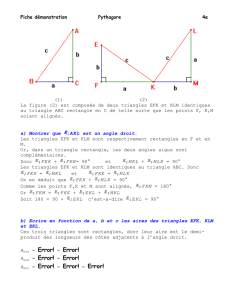
Fiche démonstration Pythagore 4e (1) (2) La figure (2) est composée

Fiche démonstration Pythagore 4e
(1) (2)
La figure (2) est composée de deux triangles EFK et KLM identiques
au triangle ABC rectangle en C de telle sorte que les points F, K,M
soient alignés.
a) Montrer que Æ;AKL est un angle droit.
Les triangles EFK et KLM sont respectivement rectangles en F et en
M.
Or, dans un triangle rectangle, les deux angles aigus sont
complémentaires.
Donc Æ;FEK + Æ;FKE= 90° et Æ;MKL + Æ;MLK = 90°
Les triangles EFK et KLM sont identiques au triangle ABC. Donc
Æ;FEK = Æ;MKL et Æ;FKE = Æ;MLK
On en déduit que Æ;FEK + Æ;MLK = 90°
Comme les points F,K et M sont alignés, Æ;FKM = 180°
Or Æ;FKM = Æ;FKE + Æ;EKL + Æ;MKL
Soit 180 = 90 + Æ;EKL c’est-à-dire Æ;EKL = 90°
b) Ecrire en fonction de a, b et c les aires des triangles EFK, KLM
et EKL.
Ces trois triangles sont rectangles, donc leur aire est le demi-
produit des longueurs des côtés adjacents à l’angle droit.
AEFK =
Error!
=
Error!
AKLM =
Error!
=
Error!
AEKL =
Error!
=
Error!
=
Error!

c)Démontrer que le quadrilatère EFML est un trapèze
Le triangle EFK est rectangle en F : (EF) ┴ (FK)
Le triangle KLM est rectangle en M : (KM) ┴ (ML)
Les points F,K,M sont alignés : (FK) = (KM)
Si deux droites sont perpendiculaires à une même troisième, alors
elles sont parallèles entre elles.
Donc (EF) // (ML).
Le quadrilatère EFML a deux côtés opposés parallèles, donc c’est un
trapèze.
d) Calculer l’aire de EFML de deux façons
1ère façon : formule de l’aire du trapèze :
Error!
soit ici :
Error!
=
Error!
=
Error!
2ème façon : somme des aires des trois triangles :
AEFK + AKLM + AEKL =
Error!
+
Error!
+
Error!
=
Error!
+
Error!
e) Conclure
On a calculé l’aire du trapèze de deux façons, on peut égaliser les
deux expressions ainsi obtenues :
Error!
=
Error!
+
Error!
ñ
Error!
=
Error!
+
Error!
ñ a2+2ab+b2=2ab+c2
ñ a2+b2=c2
La relation du théorème de Pythagore est ainsi démontrée.