Nouvelle approche pour obtenir une non-réciprocité

C
Co om mi it té é N Na at ti io on na al l F Fr ra an nç ça ai is s d de e R Ra ad di io oé él le ec ct tr ri ic ci it té é S Sc ci ie en nt ti if fi iq qu ue e
S
Se ec ct ti io on n f fr ra an nç ça ai is se e d de e l l’ ’
U
Un ni io on n R Ra ad di io o S Sc ci ie en nt ti if fi iq qu ue e I In nt te er rn na at ti io on na al le e
Siège social : Académie des Sciences, Quai de Conti – Paris
J
JO OU UR RN NÉ ÉE ES S S SC CI IE EN NT TI IF FI IQ QU UE ES S D DU U C CN NF FR RS S
"
" N NA AN NO OS SC CI IE EN NC CE ES S E ET T R RA AD DI IO OÉ ÉL LE EC CT TR RI IC CI IT TÉ É" "
P
PA AR RI IS S, , L LE ES S 2 20 0 E ET T 2 21 1 M MA AR RS S 2 20 00 07 7
Novel improved design for optical non-reciprocity in 2D magnetophotonic
crystals
Nouvelle approche pour obtenir une non-réciprocité optique améliorée
dans des cristaux magnétophotoniques 2D
Mathias Vanwolleghem, Philippe Gogol, Béatrice Dagens* et Pierre Beauvillain
Institut d’Electronique Fondamentale, UMR 8622, Université Paris-Sud, Bâtiment 220, 91405 Orsay
[e-mail]
* Alcatel-Thales III-V Lab, Alcatel Thales III-V lab Route départementale 128, 91767 Palaiseau
Résumés
En utilisant la méthode d’expansion d’onde plane anisotrope, nous démontrons au sein d’un cristal
magnéto-photonique 2D l’asymétrie de la structure de bande ( (k) ( k)). Cette asymétrie permet
de concevoir des circuits nanophotoniques planairement intégrés et avec une non-réciprocité
fortement exaltée en comparaison aux guides d’ondes magnéto-optiques intégrés et non-
nanostructurés. On propose pour la première fois une approche plus efficace et technologiquement
plus aisée pour remplir les conditions nécessaires permettant de réaliser une telle asymétrie.
Using an anisotropic plane-wave expansion method first theoretical evidence of spectral band
structure asymmetry ( (k) ( k)) is obtained for 2-dimensional magnetophotonic crystals. This
band asymmetry allows the design of nanophotonic integrated circuits with improved optical non-
reciprocal functionalities as compared to traditional ridge-type magneto-optic waveguides. We
describe for the first time a novel and technologically simpler approach to fulfil the necessary
conditions to obtain such asymmetry.
Mots clés : photonic crystals, magneto-optics, non-reciprocity, band structure asymmetry, magnetic
group theory; cristaux photoniques, magnéto-optique, non-réciprocité, asymétrie de structure de
bandes, théorie de groupes magnétiques
Introduction
Les effets de résonance au sein d’un cristal photonique ont permis une forte augmentation des effets magnéto-optiques.
Inoue et al. ainsi que Fedyanin et al. [1,2] ont prédit et observé des augmentations géantes de la rotation Faraday
magnéto-optique quand un matériau ferromagnétique est inclus comme défaut au sein d’un cristal photonique 1D type
miroir de Bragg. Toutefois, peu d’études ont été effectuées sur les spécificités de la structure de bandes d’un cristal
photonique composé de matériau magnéto-optique, en particulier dans le cas de cristaux magnéto-photoniques de
dimensionnalité supérieure à l’unité. Jusque maintenant qu’un seul groupe a étudié pour la première fois des circuits
type cristaux magnétophotoniques 2D et leur structure de bandes [3] avec pour but d’obtenir une différence de vitesse
de groupe dans deux sens opposés de propagation, en autre mots obtenir la version cristal photonique de l’effet
magnéto-optique de Kerr. Ainsi ils ont prouvé que la magnitude de cet effet Kerr est exalté au moins d’un ordre de
grandeur dans un circuit type cristal photonique, par contre nécessitant un aménagement particulier de la distribution de

l’aimantation dans la cellule d’unité du cristal. Notre apport à ces résultats est de démontrer théoriquement qu’une non-
réciprocité d’au moins la même magnitude, voire plus forte, peut être obtenue même avec une aimantation uniforme en
introduisant de manière périodique une déformation contrôlée de la cellule d’unité du cristal. Cette nouvelle approche
est parfaitement compatible avec les possibilités actuelles des technologies de nanofabrication.
Réseau hexagonal et profil de
l’aimantation
Operations de symétries présentes
Groupe magnétique
Zone de Brillouin + partie
irréductible
x
x’x’’ y
y’
y’’
1 , 2z , +3z , -3z , +6z , -6z ,
R °
x ,
R °
x’ ,
R °
x’’ ,
R °
y ,
R °
y’ ,
R °
y’’
C6v(C6) = C6 + R ° (C6v - C6)
kx
ky
K
M
x
y
1 ,
x ,
R °
y ,
R ° 2z
C2v(CS) = CS + R ° (C2v – CS)
kx
ky
K
M
x
y
1 , R ° 2z
C2(C1) = C1 + R ° (C2 – C1)
kx
ky
K
M
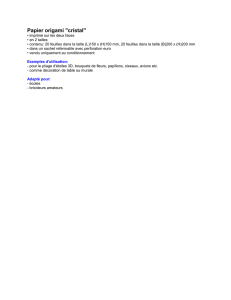
Fig. 1 : Illustration de l’évolution des opérations de symétries dans des réseaux hexagonaux magnétiques sous l’influence de rupture
de symétrie magnétique ou spatiale. Le symbole R indique l’opération de renversement de temps (qui renverse la direction du
vecteur axial de l’aimantation). Note que ce caractère axial implique aussi que l’aimantation se renverse sous une opération de
miroir parallel à ce vecteur. La troisième colonne illustre avec combien d’autres points un point k quelconque dans le BZ est
équivalent (c’est-à-dire possède la même valeur propre pour la fréquence). Ceci détermine la partie irréductible du zone de Brillouin
(IBZ). Cette partie est indiquée en gris. Une non-réciprocité dans toutes les directions ne peut donc être obtenue que si l’IBZ égale
BZ (comme dans le dernier cas).
1. Asymétrie de structure de bandes : conditions nécessaires
Figotin a été le premier à établir les conditions nécessaires pour l’observation d’une structure de bandes asymétrique
[4]. Cette condition est l’absence de toute opération de symétrie présente dans le groupe de symétrie du cristal magnéto-
photonique qui puisse transformer le vecteur d’onde kB de la fonction de Bloch en son opposé -kB. Dès que cette
possibilité existe dans le cristal magnétophotonique, la structure de bandes est nécessairement symétrique dans cette
direction particulière.
Afin d’introduire l’effet de décalage de phase Kerr non-réciproque dans un guide d’onde avec cristal magnéto-
photonique 2D, il faut appliquer l’aimantation perpendiculaire au plan du réseau. Ainsi, on évite un couplage non-
réciproque de type Faraday entre les mode Bloch de polarisation TE et TM. Dans une telle configuration magnétique la
vitesse de groupe et le phase des modes Bloch de polarisation TM (champ magnétique perpendiculaire au plan du
réseau) peuvent être différents dans les deux sens opposés de propagation, tandis que les modes TE ne seront jamais
affectées par l’aimantation. Cependant la zone de Brillouin irréductible (IBZ) d’un cristal magnéto-photonique 2D à
base d’un réseau hexagonale de trous d’air gravé dans un grenat de fer (à titre d’exemple) et soumis à une aimantation
perpendiculaire uniforme n’est pas différent de celle du cristal isotrope équivalent. Ceci est dû au fait que le champ
magnétique est un vecteur axial (et donc ne change pas de sens sous une inversion spatiale). En autre mots, sans brisure
de la symétrie magnétique et/ou du réseau spatial, un cristal magnétophotonique 2D à effet de Kerr sera toujours
réciproque (voir la Figure 1).

2. Décalage de phase Kerr non-réciproque dans un cristal magnéto-photonique.
La figure 1 illustre comment il est possible d’augmenter l’ IBZ d’un cristal magnétophotonique hexagonal, et ainsi
d’éliminer les symétries de type kB kB.
2.1. Antisymétrie de l’aimantation dans la cellule
La première approche consiste en appliquant une distribution d’aimantation antisymétrique dans la cellule d’unité.
Parce que le champ magnétique est un vecteur axial, il change de sens sous une opération de miroir dans un plan
parallel au champ. Par conséquence les seuls symétries qui restent présentes dans ce type de cristal, sont l’identité et
l’opération de miroir dans le plan x. Le cristal établira donc l’effet Kerr non-réciproque pour les modes Bloch TM dans
toutes les directions (sauf dans la direction y). Mathématiquement dans le vocabulaire de la théorie des groupes
magnétiques un tel cristal possède la symétrie du groupe de Shubnikov C2v(CS) [5].
Cette approche a été étudié par Kono et al. [3] pour un réseau hexagonal de trous d’air gravés dans un grenat de fer
substitué de Bi (n = 2.3 et gMO = 0.005 autour de  = 1300nm), aimanté perpendiculairement et avec une paroi de
domaine magnétique selon la direction . Le taux de remplissage était de 23%. Ainsi ils ont calculé une différence de
phase non-réciproque de type Kerr (donné par kB = kB,fw  kB,bw) d’environ 3/2 rad/mm, ou une exaltation d’un ordre
de grandeur par rapport aux guides magnéto-optiques classiques [6]. Cependant, ce résultat est très susceptible au
positionnement symétrique du paroi magnétique. Une déviation de quelques pour cent résulterait dans une forte
diminuation de l’effet. Avec un pas de réseau de l’ordre de 400nm, ceci implique un contrôle du positionnement de la
paroi à l’échelle nanométrique sur plusieurs millimètres. Ceci constitue évidemment un grand verrou technologique
pour la réalisation expérimentale de tels circuits nanophotoniques non-réciproques.
2.2. Rupture de symétrie spatiale du réseau de trous
+ ++ + ++
+ ++
+ ++ + ++
+ ++
M’
K
IBZ
M
M’
K
IBZ
M
-0.003
-0.002
-0.001
0
0.001
0.002
0 0.002 0.004 0.006 0.008 0.01
k*
band 3 band 4
+ ++ + ++
+ ++ + ++
+ ++ + ++
+ ++ + ++
M
X
IBZ
M’ M
X
IBZ
M’
-0.002
-0.001
0
0.001
0.002
0.003
0.004
0 0.002 0.004 0.006 0.008 0.01
k
band 3 band 4 band 5
Fig. 2 : Calcul du décalage non-réciproque de phase de type Kerr dans un réseau déformé (hexagonal et carré). La déformation
(selon la diagonale) est de 20%. Le décalage est calculé selon la direction indiquée (M’ pour le réseau hexagonal et X pour le
réseau carré). signifie la déviation en fréquence normalisée du bord de bande (M’ ou X). k* est normalisé sur 2 /a (avec a le
pas de réseau).
Notre nouvelle approche aide à résoudre ce verrou technologique puisqu’il permet de remplir les conditions nécessaires
pour une structure de bandes asymétrique même avec un profil uniform de l’aimantation. En effet, en déplacant
périodiquement la position d’un trou central dans un réseau hexagonal aimanté perpendiculairement et de manière
uniforme, la symétrie est fortement réduite (menant à un IBZ égalant la moitié du BZ), voire même entièrement enlevée
(c’est-à-dire un IBZ égal au BZ). Mathématiquement, on crée ainsi des groupes de Shubnikov de type C2(S)(C1).
On a étudié la structure de bandes et le décalage de phase non-réciproque de type Kerr dans des réseaux ainsi déformés.
Les paramètres optiques étaient les mêmes que ceux utilisés par Kono. Le réseau était déformé selon une direction de

symétrie en déplaçant un trou central de 20% par rapport à sa position idéale. Avec un taux de remplissage de 23% cela
signifie un réseau dont la caractéristique la plus fine mesure environ 200nm, ce qui est parfaitement compatible avec les
possibilités de la nanolithographie moderne.
La méthode de calcul est basé sur un algorithme vectoriel anisotrope d’expansion en ondes planes [7]. Nos premiers
résultats démontrent que la non-réciprocité ainsi obtenue est au moins aussi large que celle calculée dans les structures
de Kono (voir Figure 2). Le décalage plotté est exprimé en unités normalisées. En effet, l’actuel décalage se calcule
donc comme suit, k = k*  2/a = k*/*  2/ , avec * la fréquence normalisée de la bande considérée. Les *
obtenues étaient autour de 0.7 pour la plupart des bandes, ce qui mène a un moyen k = 2/mm pour  = 1.3 m. Pour
certaines bandes photoniques on observe même une augmentation de 50%. En plus, on a aussi étudié l’effet de
déformation dans des réseaus avec une symétrie carrée. Nos simulations montrent que l’effet relatif de déformation est
2 fois plus important dans des cristaux avec symétrie d’ordre 6 par rapport aux cristaux de symétrie d’ordre 4. Ceci est
bien évidemment dû à la plus grande brisure de symétrie en évoluant d’un groupe d’ordre symétrique 6 à un groupe
sans symétrie.
Finalement, on remarque que les réseaux deformés sont en fait des cristaux avec une cellule d’unité contenant deux,
voire trois, « atomes » par maille élémentaire (voir les mailles élémentaires dans la Figure 2). En autre mots leur groupe
de symétrie n’est pas symmorphique. Cette dernière observation nous a récemment permis d’établir une classification
générale des effets de non-réciprocité de type Kerr pour toutes les configurations spatiales imaginables d’un cristal
magnétophotonique 2D. Ceci a été fait en utilisant la classification des réseaux planairs 2D dans les 17 types possibles,
qui est connue dans la littérature de la théorie des groupes sous le nom de « wallpaper groups » [8].
Conclusion
On a proposé pour la première fois une nouvelle méthode pour obtenir de la non-réciprocité de type Kerr dans un cristal
magnétophotonique 2D. Elle se distingue de et améliore sur la méthode existante de Kono en permettant l’utilisation
d’un profil d’aimantation uniforme. L’idée fondamentale est basée sur une rupture de symétrie en déformant de manière
périodique la configuration spatiale du réseau 2D. Un tel réseau est parfaitement réalisable avec les technologies
modernes de nanofabrication, et évite la nécessité de contrôler la position d’une paroi magnétique à l’échelle
nanométrique sur plusieurs millimètres.
Références bibliographiques
[1] M. Inoue, K. Arai, T. Fujii and M. Abe, J. Appl. Phys. 83, 6768 (1998).
[2] A. Fedyanin, O. Aktsipetrov, D. Kobayashi, K. Nishimura, H. Uchida and M. Inoue, J. Magn. Magn. Mater., 282,
256 (2004).
[3] N. Kono and M. Koshiba, Opt. Express. 13 (23), 9155 (2005).
[4] A. Figotin and I. Vitebskiy, Phys. Rev. B, 67 (16), 165210 (2003).
[5] A. Cracknell, Prog. Theor. Phys. 35 (2), 196 (1966).
[6] N. Bahlmann, M. Lohmeyer, H. Dötch, and P. Hertel, J. Quantum Electron. 35, 250 (1999).
[7] S. Johnson and J. Joannopoulos, Opt. Express., 8(3),173 (2001).
[8] M. Hamermesh, Group Theory, Addison-Wesley, 1962