math-chapitre-angles-inscrits-et

Mathematiques 3ème
Collection l'Essentiel
3
Angles inscrits. Polygones réguliers
Chapitre 3 :
Objectifs :
A la fin de cette leçon, l’élève doit être capable de :
- Utiliser les propriétés des angles inscrits pour :
 Justifier une égalité angulaire
 Déterminer la mesure d’un angle
- Construire un polygone régulier inscrit dans un cercle.
- Reconnaître un angle inscrit dans un cercle
A- Essentiel du Cours
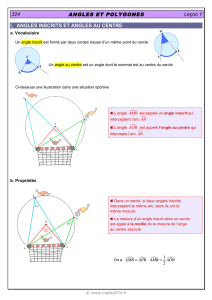
I ANGLES INSCRITS ET ANGLE AU CENTRE
1.1. Présentation
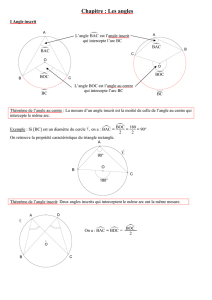
* Soit le cercle (C) A, B et M trois points de (C) l’angle
BAM
est appelé angle inscrit
dans le cercle (C)
exemples.
Dans (1) et (2) l’angle
BAM
est obtus et intercepte ce grand arc de cercle
BA
.
* Soit (C) un cercle de centre O. On appelle angle au centre tout angle dont le sommet
est le point O.
* A tout angle inscrit
BAM
, on associe un angle au centre correspondant
BAO
. Les
deux angles interceptant le même arc de cercle.
A
AN NG GL LE ES S I IN NS SC CR RI IT TS S
P
PO OL LY YG GO ON NE ES S R RE EG GU UL LI IE ER RS S
(2)
M
A
B
(1)
A
B
M
O
O
(3)
O
M
A
B
(2)
M
A
B
O
(1)
A
B
M
O
(3)
O
M
A

Mathematiques 3ème
Collection l'Essentiel
3
Angles inscrits. Polygones réguliers
1.2. mesure d’un angle inscrit
BAM
et
BAN
sont des angles inscrits dans le cercle C.
BAO
est l’angle au centre associé à
BAM
et
BAN
.
mes
BAM
=
2
1
mes
BAO
(
BAM
est un angle aigu)
mes
ANB
= 180° -
2
1
mes
BAO
(
BAN
est un angle obtu).
On constate mes
AMB
+ mes
ANB
=
2
1
mes
BAO
+ 180° -
2
1
mes
BAO
= 180°
Ainsi les angles
BAM
et
BAN
sont supplémentaires
1.3. Angles inscrits interceptant le même arc.
Propriétés :
P1 : Dans un cercle, deux angles inscrits qui
interceptent le même arc ont la même mesure.
P2 : Dans un cercle, deux angles inscrits qui
interceptent deux arcs de même longueur
ont la même mesure.
AB CD
et
mesAMB mesCMD
II- ANGLES INSCRITS ET CONFIGURATIONS DU PLAN
2.1 Propriété
Si un quadrilatère est inscriptible dans un cercle, alors ses angles opposés sont
supplémentaires.
mes
CAB 
+ mes
ACD
= 180°
mes
BDA 
+ mes
BDC 
= 180°
O
(C)
A
B
M
N
M
A
B
N
O
(2)
O
N
D
C
M
A
B
A
D
B
C
O

Mathematiques 3ème
Collection l'Essentiel
3
Angles inscrits. Polygones réguliers
2.2. Polygone réguliers
Définition : un polygone régulier est un polygone dont les côté ont même longueur et
les angles isométriques.
Polygone régulier inscrit dans un cercle.
* Construction d’un triangle équilatéral et d’un hexagone régulier :
- Marque un point A sur le cercle (C) de centre O
- Le cercle de centre A qui passe par O coupe le
cercle (C) en deux points B et F
- Les cercles de centre B et F qui passent par O
coupent le cercle (C) en deux points C et E
- Le cercle de centre E qui passe par
O coupe le cercle (C) en D.
A, C et E sont les sommets d’un
triangle équilatéral.
A, B, C, D, E et F sont les sommets
d’un hexagone régulier.
* Construction d’un carré et d’un octogone régulier.
- Marque un point A sur un cercle (C) de centre O
- Construis le diamètre [AC] et le
diamètre [BD] qui ont des supports perpendiculaires.
A, B, C et D sont les sommets d’un carré
- Construis les bissectrices des angles
BAO
et
CBO 
. On obtient les points E, F, G
et H sur le cercle (C).
A, E, B, F, C, G, D et H sont les sommets d
’un octogone régulier convexe.
Notons que :
* Tout polygone régulier est inscrit
dans un cercle et circonscrit à un
autre ; les deux cercles ayant le même centre.
B. EXERCICES
3.1. A, B, C et D sont quatre points dans cet ordre d’un cercle de centre O on donne
mes
DBO 
= 130°
1- Calculer mes
DBA 
= 130°
2- Montre que
DBA 
et
DBC 
sont supplémentaires
O
D
C
B
O
A
E
F
B
E
A
H
D
G
C
F
O

Mathematiques 3ème
Collection l'Essentiel
3
Angles inscrits. Polygones réguliers
3.2. A, B, C et D sont placées dans cet ordre sur un cercle de centre O. On donne mes
CBO 
= 140°
1. Calcule mes
CBA 
2. Montre que mes
BAC
= mes
BDC
.
3.3. Donne le programme de construction d’un pentagone régulier et construis le
3.5. Soit ABC un triangle. Un cercle de centre O passe par B et par C et recoupe
[AB] en D et [AC] en E.
Fais une figure puis démontre que
BDC
=
CEB
et
EBA
=
DCA
.
3.6. (C) est un cercle de centre O.
A, B, C, D, et E sont des points de ce cercle.
1) Cite les angles inscrits de sommet A.
2) Cite les angles inscrits ayant pour sommet
un point autre que A et qui interceptent le
même arc qu’un angle inscrit de sommet A.
3.7. ABC est un triangle isocèle en A inscrit dans un cercle (C) de centre O tel que
l’angle
CBA 
soit aigu D est le point diamétralement opposé à B.
1) Démontre que mes
BAD
= mes
CAB 
2) Démontre que les angles
ADC 
et
BAD
sont complémentaires.
3.8. Les polygones suivants sont des polygones réguliers inscrits dans un cercle.
Complète le tableau ci-dessous.
Polygone
Angle au centre en O
Angle au sommet associé en
degré
Pentagone
Hexagone
Octogone
Ennéagone
3.4. A, B, C et D sont placés dans cet ordre sur un cercle de centre O. Démontre
que les angles
BAD
et
BCD
sont des angles supplémentaires.
E
A
B
C
D
o

Mathematiques 3ème
Collection l'Essentiel
3
Angles inscrits. Polygones réguliers
Décagone
Dodécagone
3.9. Dans la figure codée ci-contre, démontre que les angles
EAF
et
EBF
sont
supplémentaires.
3.10. Calcule le périmètre et l’aire d’un octogone régulier inscrits dans un cercle de
5cm de rayon.
3.11. Construis un triangle ABC tel que BC = 7cm,
CAB 
= 70° et
BAC
= 55°. Construis
son cercle circonscrit. Soit O le centre de ce cercle. Calcule la mesure de l’angle
CBO 
.
3.12. ABCDEFG est un heptagone composé de deux carrés et de trois triangles
équilatéraux.
ABCDEFG est-il un polygone régulier ? Justifie ta réponse.
3.13. I est le centre du cercle circonscrit au triangle EFG. Calcule
EGF
. En
déduire
EIF
.
A
F
B
E
B
C
A
G
F
E
D
O
(C)
G
E
F
I
750
370
I