Amérique du Nord - Descartes et les Mathématiques

Bac S 2004
Amérique du Nord
Page 1/7
Descartes et les Mathématiques
Bac S Amérique du Nord 2004
Barycentre – Plan complexe – Probabilité – Fonction et calcul de e.
Annales bac S non corrigées : http://debart.pagesperso-orange.fr/ts/terminale.html
Document Word : http://www.debart.fr/doc/bac_2004/bac_s_amerique_2004.doc
BACCALAUREAT GENERAL Session 2004
Épreuve : MATHEMATIQUES
Série : S Durée : 4 heures Coef. : 7 ou 9
OBLIGATOIRE et SPÉCIALITÉ
L'utilisation d'une calculatrice est autorisée.
Le sujet est composé de 3 exercices indépendants.
Le candidat doit traiter tous les exercices.
La qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante
dans l'appréciation des copies.

Bac S 2004
Amérique du Nord
Page 2/7
Descartes et les Mathématiques
EXERCICE 1 (3 points)
Commun à tous les candidats
Dans le plan affine, on considère ABC un triangle rectangle en A, I le milieu du segment [AB] et J
le centre de gravité de ABC.
Pour tout réel m, différent de −
3
1
, on note Gm le barycentre du système de points pondérés
Sm = {(A, 1), (B, m), (C, 2m)}.
Pour tout point M du plan on note
M
V
= 3
MA
-
MB
-2
MC
.
Pour chacune des six affirmations suivantes, dite si elle est vraie (V) ou fausse (F). Chaque bonne réponse
donne 0,5 point, chaque réponse fausse ou illisible enlève 0,25 point, l’absence de réponse ne rapporte ni
n’enlève aucun point. Un éventuel total négatif serait ramené à 0.
Répondre aux affirmations sur la page annexe.
Affirmation
V ou F
G1 est le milieu du segment [CI].
~ G1 est barycentre de {(J, 2), (C,
3
2
)}
Pour tout point M,
M
V
=
AB
+2
AC
.
Pour tout m, distinct de −
3
1
,
m
AG
est colinéaire à
1
AG
2
1
IBG
est un triangle rectangle.
2
Pour tout point P de (AG−1), il existe un réel m tel
que P = Gm.

Bac S 2004
Amérique du Nord
Page 3/7
Descartes et les Mathématiques
EXERCICE 2 (5 points)
Candidats n’ayant pas suivi l’enseignement de spécialité
Le plan complexe est muni d’un repère orthonormal direct (O,
u
,
v
).
1. On veut résoudre dans C l’équation
(E) : z3 +4z2 +2z −28 = 0.
a. Déterminer deux réels a et b tels que l’équation (E) s’écrive :
(z − 2)(z2 + az + b) = 0.
b. Résoudre (E)
2. On note (H) l’ensemble des points M du plan complexe d’affixe z vérifiant:
z2 −4 = 4−
z
2.
a. On note x et y les parties réelle et imaginaire de l’affixe z d’un point M.
Montrer que: M appartient à (H) si et seulement si
x2 − y2 = 4.
b. Soient A, B et C les points d’affixes respectives 2, −3 − i
5
et −3 + i
5
.
Vérifier que A, B et C appartiennent à (H).
3. Soit r la rotation de centre O et d’angle −
4
.
a. Déterminer les affixes de A’, B’ et C’, images respectives de A, B et C par la rotation r (on
donnera ces affixes sous la forme algébrique).
b. On note M’ l’image par r du point M d’affixe z. On note z’ l’affixe de M’.
Les parties réelle et imaginaire de z sont notées x et y, celles de z’ sont notées x’ et y’.
On note (H’) l’ensemble des points du plan dont l’antécédent par r est un point de (H).
– Exprimer x et y en fonction de x’ et y’.
– En utilisant la question 2. a. prouver que : M’ appartient à (H’) si et seulement si
x’y’ = − 2.
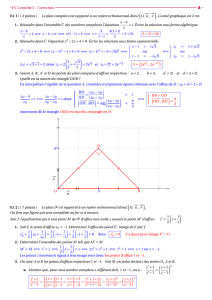
4. Faire une figure sur laquelle on placera les points A, B, C, A’, B’, C’, la courbe (H’), puis la
courbe (H).

Bac S 2004
Amérique du Nord
Page 4/7
Descartes et les Mathématiques
EXERCICE 2 (5 points)
Candidats ayant suivi l’enseignement de spécialité
Le plan complexe est muni d’un repère orthonormal (O,
u
,
v
).
Soient les points A, A’, B et B’ d’affixes respectives :
zA = 1− 2i, zA’ = − 2+ 4i, zB = 3− i, zB’ = 5i.
1. a. Placer les points A, A’, B et B’ dans le plan complexe. Monter que ABB’A’ est un
rectangle.
b. Soit s la réflexion telle que s(A)=A’ et s(B)=B’. On note (A) son axe.
Donner une équation de la droite (A) et la tracer dans le plan complexe.
c. On note z’ l’affixe du point M’ image par s du point M d’affixe z. Montrer que
z’ = (
5
3
+
5
4
i)
z
+ 2i − 1.
2. Soit g l’application du plan dans lui-même qui à tout point M d’affixe z associe le point P
d’affixe z’ définie par :
z’ = (−
5
6
−
5
8
i)
z
+ 5 − i.
a. On note C et D les images respectives de A et B par g ; déterminer les affixes de C et D et placer
ces points dans le plan complexe.
b. Soit Ω le point d’affixe 1+i et soit h l’homothétie de centre Ω et de rapport −2.
Montrer que C et D sont les images respectives de A’ et B’ par h.
c. Soit M1 d’affixe z1 l’image par h de M, d’affixe z. Donner les éléments caractéristiques de
h−1 et exprimer z en fonction de z1.
3. On pose f = h−1 ◦ g.
a. Déterminer l’expression complexe de f .
b. Reconnaître f . En déduire une construction du point P, image par g d’un point M
quelconque donné du plan.

Bac S 2004
Amérique du Nord
Page 5/7
Descartes et les Mathématiques
EXERCICE 3 (4 points)
Commun à tous les candidats
Un jeu de hasard est formé d’un dispositif lançant de façon aléatoire une fléchette dans une cible
ayant la forme suivante:
B
B
B
B
B
B
B
B
B
J
J
J
V
V
R
R
V
V
J
J
J
B
B
B
B
B
B
B
B
B
La fléchette atteint toujours une case et une seule.
Les trente cases, blanches (B), jaunes (J), vertes (V) ou rouges (R), ont toutes la même
probabilité d’être atteintes.
– Si la fléchette atteint une case rouge, le joueur gagne 8 euros.
– Si la fléchette atteint une case verte, le joueur gagne 5 euros.
– Si la fléchette atteint une case jaune, le joueur ne gagne rien et ne perd rien.
– Si la fléchette atteint une case blanche, le joueur perd a euros, la lettre a désigne un nombre
réel positif.
1. On note X la variable aléatoire représentant le gain algébrique du joueur (compté
négativement quand il perd).
a. Donner la loi de probabilité de X.
b. Calculer a pour que le jeu soit équitable, c’est-à-dire pour que l’espérance E(X) soit
nulle.
2. Un joueur est considéré comme gagnant s’il a obtenu un gain strictement positif.
a. Quelle est la probabilité p qu’un joueur gagne ?
b. Un joueur joue 5 parties consécutives indépendantes.
Quelle est la probabilité qu’il gagne exactement 2 fois ? exactement 5 fois ?
c. Quel est le nombre moyen de parties gagnantes dans la situation décrite en 2 b ?