tp-05

Circuit RLC en régime oscillatoire…………………………………………………………………………
YRM
1
But de la manipulation :
Détermination de la valeur de la résonance du circuit RLC, et calcul de son coefficient de qualité Qo.
I – Etude du courant I en fonction de la capacité C :
Matériels utilisés :
- Un générateur de tension alternative basse fréquence GBF V = 0.5 volt , f = 2000 Hz
- Une bobine de résistance R et d’inductance L. R = 25 , L = 9 mH
- Un condensateur C variable .
- Un ampèremètre A et un voltmètre V.
1) Etude théorique :
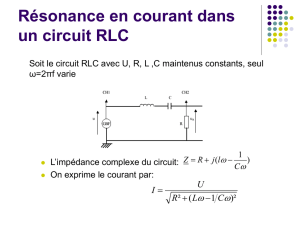
Question 1 : Montrer que V/I = R. En cas de résonance.
On sait qu’on as de résonance on a :
L0 = 1/C0 (1)
Et
V = R² - ( L0 - 1/C0 )² .I (2)
Résultat : V = R² .I
Donc : R =V/I.
Question 2 : Montrer que LC0 = 1
D’après la relation (1) - L0 = 1/C0
(1)  LC0² = 1.
2) Etude expérimentale :
*) calcule d’incertitude et erreurs commises sur les valeur :
 Tension
V = 0.001/2 = 0.0005 volt.
 Capacité :
C = Clecture = 0.001/2 = 0.0005 F
 Intensité :
I = I lecture + I appareil
I lecture :
pour le calibre 1 : I lecture = 0.02 / 4 = 0.005 F I appareil = (2.5 * 1)/100 = 0.025 F
I = 0.005 + 0.025 = 0.03 F
pour le calibre 3 : I lecture = 0.01 / 4 = 0.0025 F I appareil = (2.5 * 3)/100 = 0.075 F
I = 0.0025 + 0.075 = 0.0775 F
pour le calibre 10 : I lecture = 0.2 / 4 = 0.05 F I appareil = (2.5 * 10)/100 = 0.25 F
I = 0.05 + 0.25 = 0.3 F
pour le calibre 30 : I lecture = 0.1 / 4 = 0.025 F I appareil = (2.5 * 30)/100 = 0.75 F
I = 0.025 + 0.75 = 0.775 F
 Résistance :

Circuit RLC en régime oscillatoire…………………………………………………………………………
YRM
2
R = V/I (*)
(*)  log R = logV – log I
 d log R = d log V – d log I
 dR/R = dV/V –dI/I
 R/R = V/V + I/I
 R = R (V/V + I/I)
 Inductance :
L = (C/C)L
On fixe la fréquence f à 2 kHz et la tension à 0.5 volt.
On fait varier la valeur du condensateur C de 0 à 1.5 F par pas de 0.1 F,et on veille à chaque fois avant de lire
le courant I correspondant à C réglé de ramener la tension à 0.5 volt.
1) On établie le tableau des valeur prises :
C (F)
0
0.1
0.2
0.3
0.4
0.
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
I (mA)
0
0.72
1.9
3.2
5.8
9.8
17
19.5
19
18.5
18
16
13.5
12
11
10
I(mA)
0.03
0.03
0.0775
0.3
0.3
0.3
0.775
0.775
0.775
0.775
0.775
0.775
0.775
0.775
0.775
0.775
calibre
1
1
3
10
10
10
30
30
30
30
30
30
30
30
30
30
2) On trace la courbe I = f(C) à 2 kHz (voir la feuille millimétrée)
3) Déduire les valeur de I et de C correspondantes à l’état de résonance :
*)calcule de Iomoy
Iomoy = [(0.03*2)+(0.0775*1)+(0.3*3)+(0.775*10)]/16 = 0.549 mA
A l’état de résonance l’intensité prend la valeur de Io qui est n’est autre que le point culminant du graphe.
Io = (19.5  0.549) mA.
C = (0.7  0.0005) F .
4) On calcule R et L :
A l’état de résonance
*) R = V / I . donc
R = 0.5 / (19.5*10-3)
R = 25.64 
R = R( V/V+I/I )
R = 25.64(0.0005/0.5+0.549/19.5)= 0.747 
donc
R = (25.640.747) 
**) LC²o = 1. donc
L = 1 / C²o.
L = 1/ (0.7*10-6).4000.
L = 9.055 . 10-3
- Cacule de L :
L = L(C/C)
L = 9.055. (0.0005/0.7) = 6.46*10-3 mHenrie
donc
L = (9.0556.46*10-3 )mH

Circuit RLC en régime oscillatoire…………………………………………………………………………
YRM
3
5) Comparaison :
R inscrite = R expérimentale - c.a.d que les résistances sont les mêmes (inscrite sur la bobine et trouvée par
l’expérimentation) .
L inscrite = L expérimentale - c.a.d que les inductances sont les mêmes (inscrite sur la bobine et trouvée par
l’expérimentation) .
Conclusion:
On conclut que à l’état de résonance R ,L ,et C sont constants.
c.a.d
R inscrite = R expérimentale
L inscrite = L expérimentale
C inscrite = C expérimentale
II) – Etude du courant I en fonction de la fréquence f:
Etude théorique :
D’après la première partie , on a trouvé que :
1/Co = Lo,
en divisant sur R on aura
1/CRo = Lo/R = Qo qui est n’est autre que le coefficient de qualité.
Etude expérimentale :
Matériels a utilisé :
- Un générateur de tension alternative basse fréquence GBF V= 0.5 volt
- Une bobine de résistance R et d’inductance L. R = 25, L=9 mH
- Un condensateur C variable . C = 0.7 F
- Un ampèremètre A et un voltmètre V.
-
1) calcule d’incertitude et erreurs commises sur les valeur :
 Tension
V = 0.001/2 = 0.0005 volt.
 Capacité :
C = Clecture = 0.001/2 = 0.0005 F
 Intensité :
I = I lecture + I appareil
I lecture :
pour le calibre 1 : I lecture = 0.02 / 4 = 0.005 F I appareil = (2.5 * 1)/100 = 0.025 F
I = 0.005 + 0.025 = 0.03 F
pour le calibre 3 : I lecture = 0.01 / 4 = 0.0025 F I appareil = (2.5 * 3)/100 = 0.075 F
I = 0.0025 + 0.075 = 0.0775 F
pour le calibre 10 : I lecture = 0.2 / 4 = 0.05 F I appareil = (2.5 * 10)/100 = 0.25 F
I = 0.05 + 0.25 = 0.3 F
pour le calibre 30 : I lecture = 0.1 / 4 = 0.025 F I appareil = (2.5 * 30)/100 = 0.75 F
I = 0.025 + 0.75 = 0.775 F
 Résistance :
R = V/I (*)
(*)  log R = logV – log I

Circuit RLC en régime oscillatoire…………………………………………………………………………
YRM
4
 d log R = d log V – d log I
 dR/R = dV/V –dI/I
 R/R = V/V + I/I
 R = R (V/V + I/I)
 Inductance :
L = (C/C)/L
 Fréquence :
f = 100/4 = 25 Hz.
Avec le même montage de circuit , on fixe la capacité du condensateur à 0.7 F et on fait varier la fréquence de
1000 à 3000 Hz par pas de 200 Hz , en veillant à chaque fois avant de lire le courant I correspondant à f réglé de
ramener la tension à 0.5 volt .
1) On établie le tableau des valeur prises :*
f(Hz)
1000
1200
1400
1600
1800
2000
2200
40
2600
2800
3000
I (mA)
3
4
5.5
9
16
19.5
19
16.5
10.5
8.4
6.7
I(mA)
0.775
0.775
0.775
0.775
0.775
0.775
0.775
0.775
0.775
0.3
0.3
calibre
30
30
30
30
30
30
30
30
30
10
10
2) On trace la courbe I = f(C) à 2 kHz (voir la feuille millimétrée)
3) Déduire les valeur de Io et de fo correspondantes à l’état de résonance :
- calcule de Iomoy :
Iomoy = [(0.775*9) + (0.3*2)]/11 = 0.688 mA.
A l’état de résonance l’intensité prend la valeur de Io qui est n’est autre que le point culminant du graphe.
Io = (19.5  0.688) mA.
fo = (2000  25) Hz.
4) On calcule graphiquement le rapport fo/f1 – f2, ou f1 et f2 représentent les fréquences
correspondantes à la valeur du courant I = Io/2 :
Io = (19.5  0.688) mA.
Alors I = Io/2 = (13.780.688) mA.
f1 et f2 correspondantes à la valeur du courant I sont :
f1 = (1740  25) Hz
f2 = (2486.66  25) Hz
le rapport fo/f1 – f2est :
fo/f1 – f2= 19.5/1740 –2486.66= 2.67
On calcule Qo :
A l’état de résonance Qo = 1/RCo = Lo/R .
Qo = (9 * 10-3 * 4000)/25
Qo = 5.52
Avec
Qo =Qo.(L/L+R/R)
Qo = 5.52*7.17*10-4*7.14*10-4 = 14.31*10-4
alors

Circuit RLC en régime oscillatoire…………………………………………………………………………
YRM
5
Qo = 5.5214.31*10-4
5) On compare la valeur de Qo calculée et le rapport fo/f1 – f2 :
On trouve Qo = 2. fo/f1 – f2
Conclusion :
A l’état de résonance on trouve Qo (qui est le coefficient de qualité) , et sa valeur est de 2. fo/f1 – f2.
Question : Faut-il augmenter ou diminuer Qo pour avoir une bonne résonance ? (un pic de résonance étroit).
Réponse :
Il faut augmenter Qo pour avoir une bonne résonance.
Justification :
Pour avoir une bonne résonance (un pic de résonance étroit) , il faut que Qo soit grand , c.a.d il faut que le
rapport fo/f1 – f2soit grand , f petit fait en sorte que le pic de résonance soit étroit.