Géométrie plane : atelier de géométrie

2 BEP date
Ph. Georges Maths 1/3
GÉOMÉTRIE : FIGURES PLANES
ATELIER DE GÉOMÉTRIE
Découverte du logiciel "Atelier de géométrie 96"
Fonctions utilisées Carré Mesure Point Nommer les points
Segment (droite) Milieu (Médiatrice) Parallèle
Historique Animation
Supprimer Gomme Couleurs Épaisseurs de trait
Construction du tangram
 Enregistrer la feuille dans votre répertoire (users).
 Adopter comme nom de fichier « tangram »
I- Programme de construction
1. Tracer un carré ABCD de 10 cm de côté.
Nommer les sommets.
2. Tracer la diagonale BD.
3. Placer le point E, milieu de [BC].
Placer le point F, milieu de [CD].
Joindre les points E et Fpar un segment de droite.
4. Placer le point G, milieu de [EF].
Relier les points A et G par un segment de droite.
Placer le point d'intersection H des segments [AG] et [BD].
5. Placer le point I tel que la figure DFGI forme un parallélogramme.
6. Placer le point J, milieu de [BH].
Joindre les points E et J par un segment de droite.
II- Déplacer les points de la construction
S'assurer que la figure reste liée.
S'assurer que la figure conserve ses propriétés.
III- Imprimer l'historique de la construction si les points précédents sont vérifiés
IV- Imprimer la figure

2 BEP date
Ph. Georges Maths 2/3
GÉOMÉTRIE : FIGURES PLANES
ATELIER DE GÉOMÉTRIE
Utilisation du logiciel "Atelier de géométrie"
 Adopter comme nom de fichier le nom de la figure enregistré dans votre répertoire (users).
 Fonctions nouvelles utilisées : cercle ; zoom arrière ; longueur d'un segment ; perpendiculaire.
Programme De Construction D'un Décagone
1. Tracer un cercle de centre O et de rayon quelconque.
2. Tracer un rayon [OA].
3. Tracer le diamètre [BC] perpendiculaire à (OA).
4. Placer I le milieu du rayon [OB].
5. Tracer le cercle de centre I et de rayon IA.
6. Placer le point J, intersection du cercle de centre I et du segment [BC].
7. Placer sur le cercle de centre O des points consécutifs distants de OJ.
8. Joindre ces points par des segments de droite.
Du carré à l'octogone régulier
1. Tracer un carré MNPQ de côté 12 cm.
2. Tracer à l'intérieur du carré, les quatre quarts de cercle ayant pour centre les sommets du carré et
passant par le centre du carré.
3. Joindre les points d'intersection de ces arcs avec les côtés du carré.
 Calculer le rayon des quarts de cercle construits ; en déduire la longueur d'un côté de l'octogone.
 Montrer que le polygone est un octogone régulier (même longueur des côtés et même valeurs des
angles au sommet).
Pentagone régulier
1. Tracer un cercle © de centre O et de rayon 16 cm.
2. Tracer deux rayons perpendiculaires [OA] et [OB].
3. Placer le milieu I du segment [OA].
4. Tracer le cercle de centre i et de rayon IB.
5. Nommer J le point d'intersection du cercle © et de la demi-droite [AO).
6. La longueur du côté du pentagone est la longueur BJ.
7. Finir la construction du pentagone
 Préciser les axes de symétrie de ce pentagone régulier;
 Déterminer la mesure des angles au centre et des angles au sommet de ce pentagone.
 Déterminer l'image de ce pentagone par la rotation de centre O et d'angle de mesure 72°.
A
B
C
O
I

2 BEP date
Ph. Georges Maths 3/3
Programme de construction d'un heptagone
Le programme de construction d'un heptagone comporte 5 instructions.
Proposer l'ordre d'utilisation de ces instructions pour construire l'heptagone. Le construire.
I1 : Tracer sur le cercle C sept cordes successives de 5 cm.
I2 : Nommer O le point de concours des médiatrices du triangle.
I3 : Tracer la médiatrice de chacun des côtés du triangle équilatéral ABC.
I4 : Tracer un triangle équilatéral ABC de 10 cm de coté.
I5 : Tracer le cercle C circonscrit au triangle ABC.
 Les instructions permettent-elles de construire n'importe quel heptagone ?
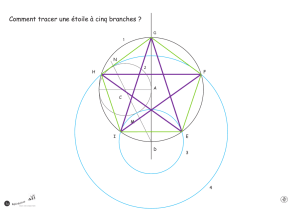
Programme de construction d'une étoile à cinq branches
La construction revient à partager le cercle en cinq secteurs égaux.
1. Tracer un segment de droite [AB].
2. Tracer le cercle C de centre O dont un diamètre est le segment [AB].
3. Tracer un diamètre [PQ] perpendiculaire au segment [AB].
4. Placer le point D milieu de [OP].
5. Tracer le cercle C1 de centre D et de diamètre OP.
6. Placer les points M et N, intersection du cercle C1 et de la droite (BD).
7. Placer les points E et F, intersection de l'arc de cercle de centre B et de rayon BM et du
cercle C.
8. Placer les points G et H, intersection de l'arc de cercle de centre B et de rayon BN et du cercle C.
9. Vérifier que les points A, G, E, F et H sont régulièrement disposés sur le cercle C.
10. Joigner ces points de manière à construire une étoile à cinq branches.
 Mesurer les longueurs AE et AG.
 Comparer le rapport
Error!
au nombre d'or soit
251
.
Programme de construction d'un ove
1. Tracer le cercle de diamètre AB.
2. Tracer la médiatrice de [AB].
3. Placer les points M et N, intersection de la médiatrice et du cercle.
4. Tracer l'arc de cercle de centre A et de rayon AB.
5. Placer le point P, intersection de l'arc et de la demi-droite [AM).
6. Placer le point Q, intersection de l'arc et de la demi-droite [BM).
7. Joigner les points P et Q par un arc de cercle de centre M.
 Préciser la nature du triangle ABM ; en déduire la mesure de l'angle ;ABM.
 Calculer les longueurs BM et MP. Calculer l'aire de l'ove.