Chapitre 8

MPSI Chapitre 8
L'ATOME D'HYDROGÈNE
8-1 Les niveaux d'énergie électronique de l'atome d'hydrogène
8-1-1 Le spectre atomique de
H
1
1
On obtient le spectre d'émission de l'atome d'hydrogène léger
H
1
1
avec un tube de Geissler contenant
de la vapeur d'eau sous très faible pression (de l'ordre de 100 Pa) et non du dihydrogène dont peu de
molécules se dissocieraient sous l'action des décharges électriques.
Ce spectre est formé de 4 raies lumineuses formant la série de Balmer. Cette série se prolonge dans
l'ultraviolet proche.
Les longueurs d'onde dans le vide de ces 4 raies sont :
 / 1nm 410,2 434,0 486,1 656,3
(violet) (indigo) (bleu) (rouge)
Les nombres d'onde dans le vide (inverses des longueurs d'onde), de la série de Balmer vérifient la
relation de Balmer
2 et m Nmavec
m
1
2
1
R
1*
22
H
RH est la constante de Rydberg de
l'hydrogène léger RH = 1,09677.107 m–1.
La longueur d'onde de la raie limite de la série de Balmer est :
nm7,364
R
2
H
2
, elle se situe dans
l'ultraviolet proche.
D'autres séries de raies ont été découvertes plus tard dans l'ultraviolet et dans l'infrarouge. Elles
vérifient toutes la formule de Balmer généralisée (1908) :
p et mNpetmavec
m
1
p
1
R
1*
22
Hp,m 
séries Lyman Balmer Paschen Brackett Pfund Humphreys
p 1 2 3 4 5 6
domaines ultra-violet visible infra-rouge
8-1-2 Spectres des autres atomes
Les spectres des atomes et ions hydrogénoïdes, c'est-à-dire qui n'ont qu'un seul électron comme
H
2
1
(hydrogène lourd ou deutérium),
H
3
1
(tritium),
He
3
2
,
He
4
2
,
26
3Li
..., sont simples et suivent la même loi
que celui de
H
1
1
:
p et mNpetmavec
m
1
p
1
RZ
1*
22
X
2
p,m 
He : Z = 2 et Li : Z = 3. RX est la constante de Rydberg correspondante et RX RH.
Pour des atomes à plusieurs électrons, les spectres sont nettement plus complexes, mais il s'agit
toujours de spectres de raies.
Pour les alcalins,
)bp( 1 )am( 1
RZ
122
X
2
a et b varient d'une série de raies à une autre.
8-1-3 L'énergie électronique, sa quantification
L'énergie d'un photon correspondant à une radiation de fréquence  est donnée par la formule
d'Einstein
 hc
c
hhE
dans laquelle h est la constante de Planck : h = 6,6262.10–34 J.s.
Lorsqu'un photon est émis par un atome dans les domaines visible, infrarouge ou ultraviolet, c'est que
l'atome perd de l'énergie électronique. Alors que les photons X, correspondant à des énergies plus élevées,
peuvent correspondre à une perte d'énergie électronique ou nucléaire et les photons , d'énergie encore plus
élevée correspondent toujours à une perte d'énergie nucléaire.

L'énergie électronique de l'atome est la somme des énergies cinétiques des électrons et de l'énergie
potentielle électrique des électrons dans le champ du noyau.
Dans son état stable l'atome est dans son état d'énergie électronique le plus bas, nommé encore
"état fondamental".
Sous l'effet des décharges électriques dans un tube de Geissler, des atomes isolés gagnent de l'énergie
électronique; ils passent dans des états excités.
L'atome peut être excité, c'est-à-dire passer à des niveaux d'énergie électronique plus élevés, dans
lesquels il reste pendant des temps très courts (de l'ordre de quelques ns). I1 revient à son état
fondamental, directement ou en cascade, en expulsant son énergie d'excitation sous la forme d'un ou de
plusieurs photons.
Le passage d'un niveau d'énergie électronique à un autre est une transition électronique.
Le fait que les spectres atomiques soient des spectres de raies et non des spectres continus montre que
les niveaux d'énergie électronique d'un atome sont "quantifiés", ce qui signifie que l'énergie électronique
ne peut prendre que certaines valeurs.
8-1-4 Interprétation du spectre d'émission de
H
1
1
Soit E1 l'énergie électronique de l'atome
H
1
1
dans son état fondamental et E2, E3..., En,... E les
énergies électronique de cet atome dans ses états excités. n est le nombre quantique principal.
Lors de la transition électronique qui fait passer l'atome
H
1
1
de Ep à Em (avec p > m), celui-ci émet un
photon d'énergie Ep – Em = h c m,p =
22
Hp
1
m
1
hcR
. On en déduit que
te
2H
nC
n
hcR
E
.
La présence de Cte dans cette expression est due à ce que l'énergie potentielle électrique est définie à
une constante près. Quand n croît, En croît et on peut démontrer que cette croissance de En correspond à une
distance moyenne de l'électron au noyau croissante. En choisissant E = 0 (absence d'énergie électronique de
l'atome ayant perdu son électron, c'est à dire de
H
1
1
), on obtient Cte = 0.
L'énergie électronique de l'atome d'hydrogène pour la valeur n de son nombre quantique principal est
donc :
2
1
2H
nn
E
n
hcR
E
L'énergie électronique dans l'état fondamental est E1 = – h c RH = 2,17872.10–18 J = – 13,5984 eV.
On ne retiendra que l'approximation suivante :
eV6,13E1 
,
2
nneV6,13
E
.
Le spectre d'émission de l'atome contient les raies correspondant à toutes les transitions
électroniques (mais il n'y en a que 4 dans le domaine visible) car l'atome peut passer par absorption d'énergie
dans n'importe quel état excité et revient à son état fondamental directement ou à la suite de plusieurs
transition (désexcitation en cascade).
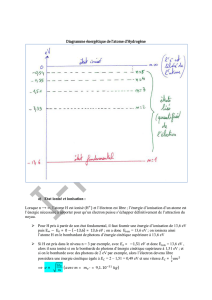
8-1-5 Spectre d'absorption, énergie d'ionisation de
H
1
1
Le spectre d'absorption d'un atome est obtenu en irradiant la vapeur monoatomique avec l'ensemble
des radiations correspondant au domaine étudié, donc en lumière blanche pour obtenir le spectre d'absorption
dans le domaine visible. Il est constitué par des raies noires sur le fond coloré.
Le spectre d'absorption de
H
1
1
ne contient pratiquement que les raies correspondant aux
transitions de l'état fondamental vers des états excités. Ceci est dû à ce que la durée de vie d'un état excité
est très faible; un atome absorbant un photon est donc pratiquement toujours un atome dans son état
fondamental.
Les raies du spectre d'absorption de
H
1
1
suivent donc la formule de Balmer généralisée, mais avec
m = 1; ce sont les raies de la série de Lyman (toutes dans l'ultraviolet).
Lorsqu'un atome
H
1
1
absorbe un photon d'énergie 13,5984 eV (0 = 91,2 nm), il passe dans l'état
n = , son électron est donc arraché, il est ionisé.
L'énergie d'ionisation de
H
1
1
est donc
eV6,13EI 1
.

L'énergie molaire d'ionisation de
H
1
1
est donc N I = 1,31.103 kJ.mol–1.
L'atome
H
1
1
dans son état fondamental n'absorbe un photon que si celui-ci a exactement l'énergie
nécessaire pour le faire passer dans un état excité ou s'il a une énergie supérieure à l'énergie d'ionisation.
L'énergie excédentaire du photon se retrouve alors sous forme d'énergie cinétique de l'électron arraché (celle-
ci n'étant pas quantifiée). Il en résulte que le spectre d'absorption de
H
1
1
se prolonge par un spectre continu en
dessous de 0 = 91,2 nm.
8-1-6 Cas des autres atomes
Pour les atomes et ions hydrogénoïdes, le même raisonnement conduit à
2
2
nn
hcR
ZE 
. L'énergie
électronique ne dépend donc encore que du nombre quantique principal n correspondant à l'état électronique
de l'électron unique de l'atome.
Pour les autres atomes ou ions simples, l'énergie électronique dépend de la valeur de n pour chaque
électron et au moins, pour chaque électron, d'un deuxième nombre quantique l : le nombre quantique
secondaire (ou azimutal).
8-2 L'atome
H
1
1
en mécanique quantique
8-2-1 Description de l'électron dans un atome hydrogénoïde
L'approximation de la mécanique classique ou celle de la mécanique relativiste ne conviennent pas
pour un électron dans un atome, alors qu'un électron arraché peut être décrit correctement par la mécanique
classique, ou par la mécanique relativiste si sa vitesse est très grande. Il faut tenir compte de sa double
nature, corpusculaire et ondulatoire, c'est-à-dire utiliser la physique quantique. On ne peut pas préciser sa
trajectoire mais seulement sa probabilité de présence dans un volume donné.
L'électron est décrit, comme toute particule par une fonction d'onde qui est une fonction complexe de
ses coordonnées de position et de la date :
)t,z,y,x(
. La fonction d'onde est solution de l'équation de
Schrödinger qui joue en mécanique quantique un rôle analogue celui de la deuxième loi de Newton en
mécanique classique.
La signification physique de la fonction d'onde est la suivante :
La probabilité de présence de la particule dans le volume élémentaire d autour du point de
coordonnées x,y,z à la date t est donnée par : dP(x,y,z,t) =  * d
Pour une particule placée dans un champ stationnaire, la fonction d'onde peut s'écrire sous la forme
)tiexp()z,y,x()t,z,y,x( 
donc * =  exp(it) et la probabilité de présence dans d est bien
indépendante du temps : dP(x,y,z) =  * d =  * d. C'est le cas pour l'électron d'un atome
hydrogénoïde sauf pendant une transition électronique, il est en effet soumis au champ électrostatique créé
par le noyau d'expression
r4Ze
V
0
, r étant sa distance au noyau.
(x,y,z) est appelé fonction d'onde stationnaire (en fait on utilise les coordonnées sphériques, plus
pratiques) et la probabilité élémentaire de présence de l'électron dans le volume d est donc donnée par
d*dP
, avec (condition de normation)
E1d*
, E représentant tout l'espace.
Chacune des fonctions d'onde stationnaires  solution de l'équation de Schrödinger représente donc
une certaine répartition de la probabilité de présence de l'électron, donc une certaine forme du volume dans
lequel la probabilité de présence est, par exemple, de 90 % . On appelle orbitale la description géométrique
de la probabilité de présence de l'électron. Les orbitales les plus simples sont à symétrie sphérique, centrées
sur le noyau.
À chaque fonction d'onde stationnaire correspond donc une orbitale et une certaine énergie
électronique.
Plusieurs orbitales différentes (donc  différentes) peuvent correspondre à une même énergie
électronique, on dit alors qu'il y a dégénérescence des niveaux d'énergie.

8-2-2 Les nombres quantiques de l'électron dans l'atome
H
1
1
Les fonctions d'onde stationnaires de l'électron d'un atome
H
1
1
font intervenir trois nombres
quantiques notés n, l et ml.
- Le nombre quantique principal n :
Nn *
C'est le seul qui intervienne dans l'expression de l'énergie électronique de
H
1
1
:
2
1
2H
nn
E
n
hcR
E
.
On retiendra aussi que plus n est grand, plus l'orbitale s'étend loin du noyau (la distance la plus
probable du noyau à l'électron croît).
- Le nombre quantique azimutal (ou secondaire) l :
Il peut prendre toutes les valeurs entières de 0 à n – 1, soit n valeurs possibles pour n donné.
Il intervient dans la quantification de la norme du moment cinétique orbital de l'électron. Avec O,
position du noyau, m, masse de l'électron, M, sa position et
v
, sa vitesse, on a :
 vmOML0
,
 2
h
)1l(lL0
.
Les fonctions d'onde correspondant à l = 0 1 2 3 4 5 ...
sont nommées respectivement par les lettres : s p d f g h ...
Par exemple, n =2 et l = 1, l'électron est dans l'orbitale notée 2p.
- Le nombre quantique magnétique ml :
Il peut prendre toutes les valeurs entières de – l à + l, soit 2l + 1 valeurs possibles pour l donné.
Il intervient dans la quantification de la projection du moment cinétique orbital sur une direction (z'z)
(par exemple, celle du champ magnétique) :
2
h
mL lz0
.
Il n'intervient dans l'expression de l'énergie qu'en présence d'un champ magnétique extérieur, ce qui
permet d'expliquer le dédoublement que subissent alors certaines raies (effet Zeeman).
Les dénominations des 3 orbitales p sont px, py et pz, celles des 5 orbitales f sont dxy, dyz, dzx,
2
z
d
et
22 yx
d
... mais il n'existe qu'un seul type d'orbitale s.
Le nombre d'orbitales correspondant à une valeur de n est
2
1n
0n)1l2( 
.
- Le spin de l'électron s :
La norme du moment cinétique propre d'une particule (calculé au point où se trouve la particule) est
quantifiée par son nombre de spin s, qui est toujours un multiple positif ou nul de
2
1
.
 2
h
)1s(sLp
.
Pour l'électron
2
1
s
et
4
h
3Lp
.
- le nombre quantique magnétique de spin ms :
Il peut prendre les valeurs
2
1
et
2
1
.
Il intervient dans la quantification de la projection du moment magnétique propre sur une direction
(z'z) (celle du champ magnétique par exemple) :
2
h
mL spz
.
La valeur de ms influe très légèrement sur l'énergie électronique, il en résulte un dédoublement de
certaines raies, mais les deux raies sont alors très voisines (par exemple la raie  de
H
1
1
est en fait formée de
deux raies dont les longueurs d'onde ne diffèrent que de 0,01 nm); c'est la structure fine du spectre. Il existe
aussi une structure hyperfine du spectre due à ce que le noyau de
H
1
1
crée aussi un champ magnétique qui
interagit avec l'électron.

8-2-3 Conclusion
Pour une valeur donnée de n, donc (en première approximation) pour une énergie électronique
donnée de l'atome
H
1
1
, il y a donc n2 orbitales différentes, c'est à dire n2 répartitions possibles de la
probabilité de présence de l'électron dans l'espace autour du noyau; mais il y a 2 n2 états différents possibles
de l'électron, en tenant compte du spin : il y a 2 n2 "spin-orbitales".
Il en est de même pour tous les atomes et ions hydrogénoïdes : mais, avec l'approximation RX RH,
les niveaux d'énergie sont tous multipliés par Z2 par rapport à ceux de
H
1
1
.
Niveaux d'énergie, orbitales et transitions électroniques pour
H
1
1
-13,6
-3,4
-1,5
-0,85
-0,54
1s
2s 2px 2py 2pz
3s 3px 3py 3pz 3dxy 3dyz 3dzx 3dz23dx2-y2
4s 4px 4py 4pz 4dxy 4dyz 4dzx 4dz24dx2-y24f
E / eV
Lyman (UV)
Balmer (vis,UV)
Paschen(IR)
Brackett(IR)
etc..
-13,6
-3,4
-1,5
-0,85
-0,54
1s
2s 2px 2py 2pz
3s 3px 3py 3pz 3dxy 3dyz 3dzx 3dz23dx2-y2
4s 4px 4py 4pz 4dxy 4dyz 4dzx 4dz24dx2-y24f
E / eV
-13,6
-3,4
-1,5
-0,85
-0,54
1s
2s 2px 2py 2pz
3s 3px 3py 3pz 3dxy 3dyz 3dzx 3dz23dx2-y2
4s 4px 4py 4pz 4dxy 4dyz 4dzx 4dz24dx2-y24f
E / eV
Lyman (UV)
Balmer (vis,UV)
Paschen(IR)
Brackett(IR)
etc..