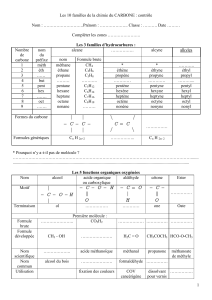
BIOT au début du 19ème siècle avait constaté une étrange propriété

BIOT au début du 19ème siècle avait constaté une étrange propriété de l'acide tartrique naturel, qu'il ne
put interpréter, le pouvoir rotatoire. Cette molécule en solution dans l'eau, certains cristaux comme le
spath d'Islande, ne sont pas transparent comme le verre ou les liquides.
La lumière naturelle est une onde électromagnétique qui se propage linéairement, mais elle n'est que
rarement simple. Comme toute onde elle est définie par sa fréquence ou sa longueur d'onde, son
amplitude, sa phase, son plan de vibration. La lumière naturelle est un mélange d'ondes de
caractéristiques différentes. Par contre si la longueur d'onde (et la fréquence qui lui est reliée) est
unique, la lumière est monochromatique, d'une seule couleur. Si toutes les ondes sont en phase elle est
cohérente. Si le plan de vibration est unique et constant elle est polarisée. Ceci peut être obtenu par
une réflexion selon un angle particulier, ou par la transmission à travers un cristal particulier
(polariseur).
Une molécule douée de pouvoir rotatoire modifie le plan de vibration de l'onde lumineuse, sans en
changer la direction de propagation.
Le montage est le suivant:
1erpolariseur
et sens de
propagation
plan de
polarisation
solution
de
composé
actif
plan
dévié
polariseur
mobile
rotatif
plan dévie
de
degrés
pour
observateur
situé à
droite
Biot en tira les conclusions quantitatives suivantes dites Loi de Biot.
Lorsqu'un faisceau de lumière polarisée, selon un plan longitudinal, traverse un milieu contenant
un isomère optique le plan de polarisation de la lumière est dévié d'un angle . qui est
proportionnel à l'épaisseur de substance traversée (d), et à la concentration de la solution du corps (c).
Dans le cas général d'un composé en solution dans un solvant optiquement inactif on a:
= [ ].l.c Loi de BIOT
avec [ ]: pouvoir rotatoire spécifique mesuré en degrés.
l: largeur de la cuve (trajet optique) en dm. c: concentration de substance active en g/mL
Une substance faisant tourner le plan de polarisation de la lumière est dite "douée d'un POUVOIR
ROTATOIRE", ou encore OPTIQUEMENT ACTIVE.
L'angle est compté positivement vers la droite (cas de la figure, observateur face au rayon sortant).
> 0 vers la droite , le composé est dit DEXTROGYRE et noté (+)(préferable) ou (d)(déconseillé par
UICPA).

> 0 vers la gauche le composé est dit LÉVOGYRE et noté (-) ou (l).
Ex: acide (d) lactique ou acide (+) lactique.
Deux isomères optiques possèdent les mêmes propriétés chimiques et beaucoup de propriétés
physiques (point d'ébullition, de fusion, indice de réfraction, conductivité électrique etc.) identiques.
Ces propriétés sont dites scalaires parce qu'elles sont représentées en un point de l'espace par un
nombre. Par contre, les propriétés physiques de nature vectorielles (polarisation rotatoire de la lumière,
piézo-électricité) seront différentes pour les deux énantiomères.
Deux antipodes optiques ou deux énantiomères purs ont des pouvoirs rotatoires spécifiques égaux en
valeur absolue et de signes opposés (optiquement purs).
Lorsqu'on a autant de molécules dextrogyres que de molécules lévogyres le mélange est optiquement
inactif, il est appelé MÉLANGE RACÉMIQUE. ([A(+)]= [A(-)]).
Il est noté (d, l) ou (±).
Ex : Acide (d, l) tartrique.
PASTEUR, vers 1848, en travaillant sur les fermentations du vins eut à analyser un sel de l'acide
tartrique inactif sur la lumière polarisée, le tartrate double d'ammonium et de sodium. (l'acide tartrique
est un diacide). Pour le purifier il en fit une solution saturante à 27° qu'il fit recristalliser lentement. Il
constata que le solide précipité présentait deux formes cristallines symétriques l'une de l'autre par
rapport à un plan. Il sépara aux pinces brucelles les deux types de cristaux. Il refit une solution aqueuse
de chacun et constata que chaque solution présentait un pouvoir rotatoire, les deux angles de rotation
étant opposés.
Il en tira l'hypothèse suivante: comme le deux types de cristaux sont symétriques et que les propriétés
des deux sels sont identiques, c'est que l'arrangement spatial des atomes dans le cristal est la cause de la
dissymétrie de chacun des deux types de cristaux. Cette caractéristique doit se retrouver dans la
molécule et elle est la cause des pouvoirs rotatoires opposés des deux formes de l'acide tartrique.
Plus généralement, les propriétés des molécules ne sont pas uniquement dues à la nature des atomes
les composant, ni à leurs proportions respectives. La disposition spatiale des atomes dans la
molécule est une des cause de leurs différentes propriétés.
Cette hypothèse implique et renforce la théorie atomique qui ne s'imposera que un demi siècle plus
tard. Il faut bien comprendre que cette hypothèse est exprimée 25 ans avant que Le Bel et van t'Hoff ne
formulent l'idée que le carbone donne des liaisons tétraèdriques.
C'est en acceptant cette hypothèse en tant que représentation performante de la matière que nous
continuons le cours.
POINT DE VUE GEOMETRIQUE, GENERALITES.
Si on doit faire un modèle spatial des molécules, cela entraîne des conséquences géométriques liés à la
nature de l'espace tridimensionnel.
Tout objet dans lequel on pourra identifier trois directions indépendantes, existe sous deux formes
différentes car non superposables.
Ex trièdre trirectangle direct, trièdre inverse.

Dans un trièdre direct plaçons un tétraèdre, puis inversons une direction.
fig I fig II
Les deux figures obtenues sont symétriques par rapport à un plan, on dit images l'une de l'autre dans un
miroir, ou encore images spéculaires. Elles sont inverses dans l'espace à trois dimensions, et ne sont
pas superposables par une opération de déplacement dans cet espace.
Pour faire se superposer les points 1 et 2 , il faut faire tourner autour d'un axe vertical de 90° la
figure II, et déplacer l'ensemble vers la gauche. Si 1 et 2 se superposent bien, par contre le point 3 de
la figure II ira se placer sur le point 4 de la figure I et e point 4 de la figure II ira se placer sur le point 3
de la figure I .
Cette propriété est entre autre celle de la main qui peut être droite ou gauche, on appelle chiralité cette
caractéristique et les objets qui la possède, objet chiraux. En fait c'est une propriété de l'espace,
absolument générale, qui n'est que quelques fois cachée par une ou des symétries de l'objet.
Exemple, main, pied, oreille, coquille d'escargot, etc.
objets symétriques: boules, cubes, objets plans, ensemble du corps humain etc.
La majorité des molécules possédant un nombre de carbones élevé, sera le plus souvent chirales et
donnera deux isomères topologiquement identiques.
Remarque. Ceci sera observable que si on peut différencier les points les uns des autres, le fait que
le point 3 et le point 4 soient permuté n'a de conséquenses physiques que si les objets qui occupent ces
coordonnées sont physiquement différents. On dit discernables. S'ils sont identiques on ne peut pas
constater de permutation. Or si c'est le cas, par exemple 3 et 4 sont identiques, l'objet représenté par les
4 points 1,2,3,4 possède une propriété de symétrie. Ici une symétrie par rapport à un plan vertical
passant par les points 1 et 2 et dont les points 3 et 4 sont situés à égale distance sur la même
perpendiculaire.
D'autres symétries, mais pas toutes, rendent indiscernable un objet de son image spéculaire.
D'où la conclusion toute figure à trois dimensions est chirale, sauf si elle possède une symétrie qui la
rend superposable à son image dans un miroir.

FORME de L'ATOME de CARBONE
Si des molécules carbonées simples, avec 3ou 4 atomes de carbone peuvent présenter un pouvoir
rotatoire, cela implique une structure tridimensionnelle de l'atome de carbone. Le Bel et Vant'Hoff,
indépendamment ont donc proposé une forme tétraédrique. Celle ci fut par la suite remplacée par une
structure ou le carbone est situé au centre d'un tétraèdre régulier, tandis que les substituants occupaient
les sommets.
On comprendra plus aisément à partir d'exemple.
Si le carbone a une structure symétrique, il n'existe qu'un seul isomère monosubstitué du méthane. Ce
que confirme l'expérience.
Deux cas sont alors possibles, une forme carré plan, une forme tétraédrique.
Si c'est un carré plan il doit exister deux isomères bisubstitués du méthane
Si c'est un tétraèdre il ne doit exister qu'un isomère bisubstitué du méthane
L'expérience n'a jamais mis en évidence qu'un seul isomère bisubstitué du méthane.
ATOME de CARBONE ASYMETRIQUE, CENTRE D'ASYMETRIE.
Un atome de carbone tétraédrique sp3 portant quatre substituants différents a, b, c, d donnera lieu
généralement à une isomérie optique.
En effet ces deux composés ne peuvent se superposer, que si deux au moins des substituants sont
identiques.
Un atome de carbone portant 4 substituants différents est appelé Carbone asymétrique sa présence dans
une molécule peut entraîner une isomérie optique.
Attention: Il existe des molécules ayant des carbones asymétriques et qui ne présentent pas d'isomérie
optique.
Le carbone asymétrique est noté C* il est appelé Centre Asymétrique.
1°) Si une molécule et son image dans un miroir ne sont pas superposables, on dira qu'une telle
molécule présente une ISOMÉRIE OPTIQUE.

On démontre mathématiquement que tout objet qui a un plan, un centre ou un axe inverse de symétrie
est superposable à son image dans un miroir.
(L'axe inverse de symétrie d'ordre n correspond à une rotation de 360°/n autour d'un axe, suivie d'une
réflexion par rapport à un plan perpendiculaire à cet axe).
2°)Si une molécule n'a ni plan, ni centre, ni axe inverse de symétrie elle présente donc une
isomérie optique.
Attention: un axe simple de symétrie ne possède pas cette propriété.
Dans ce cas la molécule asymétrique pourra exister sous deux formes différentes non superposables
appelées configurations, énantiomères, ou antipodes optiques.
Attention: Ne pas confondre configuration et conformation, cette dernière s'applique à deux ou
plusieurs formes géométriques d'une même molécule, on passe de l'une à une autre sans rupture de
liaison, mais par simple rotation des substituants autour des liaisons AUTRES ATOMES. L'azote
est décrit par une structure pyramidale, qui devrait conduire à un isomérie géométrique analogue au
carbone. Mais il existe un équilibre rapide à température ambiante entre deux formes qui rend cette
isomérie inobservable. Si par contre une liaison, ou d'autres causes, rend cet équilibre impossible,
l'azote est alors centre d'asymétrie. Ceci ne concerne pas le phosphore l'équilibre d'inversion des
phosphines étant plus lent que celui des amines. Voir aussi O et S tricoordinés.