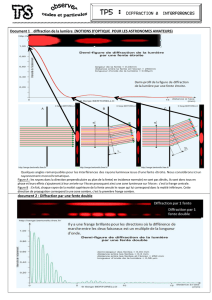
I – Observations du phénomène de diffraction

Université de Provence 2002/2003 page 1/8
MP09 : Diffraction des ondes lumineuses
Bibliographie :
SEXTANT, Optique Instrumentale, Hermann (1997)
DUFFAIT, Expériences d’optique à l’agrégation, Bréal (1994)
SURREL, Optique instrumentale - Optique de Fourier, Ellipses (1996)
PEREZ, Optique - Fondements et applications, Dunod (2000)
BREBEC, Optique ondulatoire,H prépa, Hachette supérieur (2000)
Lorsqu’un faisceau lumineux éclaire un écran opaque percé d’une petite ouverture, on
obtient pour image une tâche lumineuse dont les dimensions ne correspondent pas à l’ombre
portée. Si un faisceau tombe sur une fente, l’ouverture angulaire du faisceau émergent
augmente lorsque la largeur de la fente diminue. Ce phénomène, inexplicable par les lois de
l’optique géométrique, est appelé diffraction. Il intervient lorsque la lumière rencontre une
ouverture ou un obstacle dont les dimensions sont de l’ordre de grandeur de la longueur
d’onde.
I – Observations du phénomène de diffraction. De Fresnel à Fraunhofer.
1. Diffraction de bord d’écran
2. Approximation de Fraunhofer
II – Etude de la diffraction dans l’approximation de Fraunhofer
1. Diffraction par une ouverture rectangulaire
2. Diffraction par une structure périodique
3. Diffraction par une ouverture circulaire
a. Généralités
b. Application à la détermination de la taille des spores de lycopodes
(réseau aléatoire – Théorème de Babinet)
III – Filtrage des fréquences spatiales
1. Filtre passe-bas : Expérience d’ABBE
2. Filtre passe-haut (Strioscopie)
IV – Pouvoir séparateur d’un instrument d’optique en éclairage incohérent
Critère de Rayleigh

Université de Provence 2002/2003 page 2/8
I – Observations du phénomène de diffraction. De Fresnel à Fraunhofer
1. Diffraction de bord d’écran
On observe sur l’écran la figure suivante
qui est différente de la figure géométrique
attendue. Il y a passage progressif de l’ombre
à la lumière et éparpillement de la lumière.
2. De Fresnel à Fraunhofer
Chaque point de la surface est assimilable à une source secondaire ponctuelle et on obtient sur
l’écran la somme des ondes sphériques de chaque source.
dxdyrn
r
e
yxE
i
zyxEKirchoffdeIntégrale rki ),cos(),(
1
)',','(: 
dxdyeeyxE
z
e
i
zyxEFresneldeionApproximat z
yyik
z
xxik
ikz  
'2
)'(
'2
)'(
'22
),(
'
1
)',','(:
dxdyeyxEe
z
e
i
zyxEFraunhoferdeionApproximat z
yyxxik
z
yxik
ikz  
'2
)''(
'2
²)²(
'),(
'
1
)',','(:
Dans l’approximation de Fraunhofer, on va négliger les termes quadratiques.
Dans la pratique avec le montage du I.1., on évaluera le rapport
D
a ²
et si
D
a ²
<< 1 alors on se
trouvera bien dans l’approximation de Fraunhofer (diffraction à l’infini).
Manipulation : on ferme progressivement la fente 2 et lorsque on est certain d’avoir un sinc
on mesure alors a par projection avec une lentille.
+
M
x
y
z
x’
y’
r

Université de Provence 2002/2003 page 3/8
A.N. : D = 1 m = 550 nm a =………. d’où
D
a ²
= …………
II – Etude de la diffraction dans l’approximation de Fraunhofer
1. Diffraction par une ouverture rectangulaire
L’étude théorique nous donne :
spatialesfréquences
o
et
o
avecbcacIoI  )²(sin)²(sin
 cosinus directeurs de l’onde diffractée
 cosinus directeurs de l’onde incidente
On observe alors une croix de Mills (cf ANNEXES).
Si l’on désire calculer a, on regarde suivant x.
A l’oscilloscope : X=…… est la largeur du
capteur CCD et correspond à T=……..ms. On
compte alors k minima qui correspondent à
a
D
kx
mais à t à l’oscillo. On a alors
TtX
x
= mm. D’où
x
D
ka
=……mm
Incertitude :
T
T
tt D
D
avec
xx D
D
a
a )(
A.N. :
2. Diffraction par une structure périodique
On considère le même montage qu’en II.1., en projection sur un écran. Le réseau est obtenu
par des translations d’une fente source unique ce qui en terme de transformée de Fourier se
traduit par une modulation d’amplitude. Pour une fente on a une intensité proportionnelle à
sinc² avec une largeur du pic central
aD
L
2
. Pour deux fentes, on a une convolution
fente
txox1 *)( 
. L’intensité est alors proportionnelle à un cos² modulé par la diffraction
d’une fente.
Pour un réseau, on observe une série de pics de dirac modulés en amplitude par la figure de
diffraction d’une fente. On peut vérifier alors que la largeur du pic central est 2 X celles des
pics secondaires.

Université de Provence 2002/2003 page 4/8
3. Diffraction par une ouverture circulaire (cf ANNEXES)
a. Généralités
L’étude de l’ouverture circulaire est importante car tout objectif de caméra ou d’appareil
photo et plus généralement tous les instruments d’optique ont une symétrie cylindrique,
l’objet diffractant étant la pupille de sortie de l’instrument.
La figure de diffraction d’un trou de rayon R est une tâche d’Airy, dont le rayon angulaire 1
du premier anneau sombre est donné par le premier zéro de la fonction de Bessel (Cf
ANNEXES)
R2
22.1
1
b. Application à la détermination de la taille des spores de lycopodes.
Dans le cas des spores , le facteur de forme est l’intensité diffractée par un seul des objets
élémentaires(ie : une sphère). En pratique, on obtient la figure de diffraction par un disque
opaque qui en vertu du théorème de Babinet (Cf ANNEXES) donne le même résultat – une
figure d’Airy – qu’un petit trou circulaire.
De plus, pour N objets réparties aléatoirement, on obtient la même figure de diffraction que
pour un seul objet de rayon d, mais N fois plus intense, sauf au centre (N² fois plus intense).
D’où
RD
d
22.1
A.N. :

Université de Provence 2002/2003 page 5/8
)('
:'
doùD
R
R
D
D
d
d
eincertitudldeCalcul
III – Filtrages des fréquences spatiales
L’une des propriétés remarquables de la transformée de Fourier est : TF(TF(f(x,y))=f(-x,-y).
Par conséquent, si l’amplitude de la figure de diffraction est la transformée de Fourier de la
fonction pupillaire de l’objet alors la transformée de Fourier de la figure de diffraction est la
fonction pupillaire de l’objet. On va donc pouvoir faire des modifications de la figure de
diffraction dans le plan de Fourier et en observer les conséquences.
1. Expérience d’Abbe : Filtre passe-bas.
Manipulation :
 Prendre f1 ~ 20-25 cm et f2 = f1/2.
 Sans L1, faire l’image de l’objet par L2 sur l’écran (image peu
lumineuse)
 Mettre L1 et chercher l’image de S au travers de L1 et L2. En S’, on
a le plan de Fourier et l’on s’arrange pour que S’ ne soit pas trop
près de L2.
 L’objet diffractant est une grille pour bec Bunsen (Réseau 2D) qui a
pour figure de diffraction dans le plan de Fourier une croix de Mills.
mettre une fente diaphragme à cet endroit.
Dans le dernier cas, on a un pas dans le plan de Fourier multiplié par
2
, donc dans le plan
image, on aura un pas divisé par
2
par rapport aux traits horizontaux ou verticaux.