word - Physique

Nom : Prénom : Classe :
Contrôle de sciences physiques n°2
Calculatrice autorisée. Les exercices peuvent être traités dans le désordre.
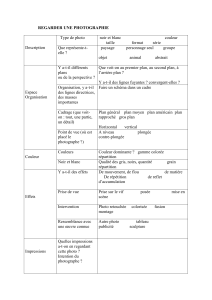
I - Extraction des colorants du paprika [ / 6 ]
On souhaite extraire les pigments responsable de la coloration du paprika. Pour cela, on place deux spatules de poudre de paprika dans 10 cm3
d'éthanoate d'éthyle. On fait chauffer le mélange en utilisant un montage de chauffage au reflux pendant 30 min. On filtre ensuite le mélange à
l'aide d'un montage de filtration simple. Enfin on réalise une chromatographie sur couche mince.
1. Définir ce qu'on entend par l'expression "faire une extraction des pigments du paprika". (/0,5)
Faire l'extraction des pigments du paprika signifie faire passer les espèces chimiques colorées du paprika dans un solvant dans lequel
ces pigments sont solubles.
2. Convertir 10 cm3 en cL. (/1,5)
10 cm3 = 10 (10-1 dm) 3 = 10. 10-3 dm3 = 10. 10-3 L = 10. 10-3. 102 L
10 cm3 = 10. 10-1 cL
3. a- Faire le schéma légendé de la filtration (/1,5)
b- Indiquer à quoi sert une filtration. (/0,5)
Une filtration sert à séparer une phase solide et une phase liquide.
4. Après élution, le chromatogramme obtenu est représenté ci-contre. La tache la plus proche du front de l'éluant a une
coloration jaune, celle du milieu est rouge et la troisième est orange. Que peut-on déduire de ce chromatogramme ?
(/0,5)
Le chromatogramme comporte 3 taches colorées séparées spatialement. On peut donc en déduire que le filtrat
contient au moins 3 espèces chimiques colorées différentes.
5. Indiquer comment il aurait fallu procéder pour vérifier que la tache jaune correspond à du β-carotène et préciser ce qu'on aurait
observé. (/1)
Pour vérifier que la tache jaune correspond à du β-carotène, il aurait fallu faire un dépôt d'une solution de β-carotène sur la ligne de
dépôt. Si les hauteurs atteintes respectivement par la tache de β-carotène et par la tache jaune étaient identiques, on aurait pu
conclure que la tache jaune était effectivement du β-carotène.
6. La formule topologique du β-carotène est donnée ci-dessous. Expliquer pourquoi le β-carotène est considéré comme une molécule
organique. (/0,5)
Cette molécule est constituée essentiellement par des atomes de carbone et d'hydrogène (chaîne carbonée). C'est donc une molécule
organique.
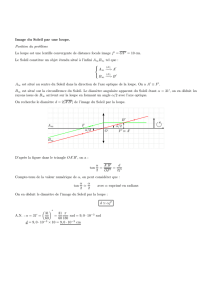
I- Optique géométrique - Loupe [ / 8 ]
Un photographe utilise une loupe pour observer un détail sur une photo. La taille du détail dont il veut faire l'image vaut
mm5,0AB 
. La loupe
est une lentille convergente de vergence C = 12,5 δ.
1. Calculer la distance focale de cette loupe. (/1)
C = 1 / f
D'où f = 1/C
AN : f = 1/12,5
f = 8,00 .10-2 m = 8,00 cm

2. Le centre optique O de la loupe est située à 6,0 cm de la photo. Calculer
OA'
où A' est l'image du point A sur le détail au travers de la
loupe. (/1,5)
f
1
OA
1
OA'
1
D'où
fOA
OA f
OA'
1
D'où
OA f
fOA
OA'
AN :
.10 2,0
.10 8,006,0.10-
OA' 2-
-22
cm24m24.10OA' 2 
3. Retrouver la valeur de
OA'
par une construction graphique. Prendre une échelle 1/2 pour l'axe horizontal et une échelle 1 pour l'axe
vertical. (/2)
4. Calculer le grandissement, noté γ. (/1)
OA
OA'
AB
B'A'
γ
En particulier
OA
OA'
γ
AN :
2
-2
6,0.10
24.10-
γ
4γ
5. Indiquer si valeur du grandissement obtenue est cohérente avec le tracé réalisé à la question 3. Justifier la réponse (/1)
Le grandissement est positif : cela est cohérent avec le tracé car sur le tracé, l'image est dans le même sens que l'objet.
Le grandissement est plus grand que 1 : cela est cohérent avec le tracé car l'image est plus grande que l'objet.
6. Indiquer s'il est possible de former l'image
B'A'
de l'objet
AB
sur un écran. Justifier la réponse et si oui, indiquer comment procéder.
(/0,5)
L'image est virtuelle : il n'est pas possible de faire directement l'image de
AB
sur un écran car les rayons ne se croisent pas après la
lentille. Tout se passe comme si ils étaient émis par une image qui serait située derrière la lentille.
Le photographe pose sa loupe et à présent regarde un oiseau.
Le schéma de l'œil du photographe est donné ci-contre. La distance entre le centre optique du cristallin et la rétine vaut 17 mm.
L'oiseau est à 150 m devant le photographe et on peut donc considérer que l'oiseau est "à l'infini" devant l'œil du photographe.
7. Déterminer quelle est la distance focale du cristallin lorsque le photographe voit l'oiseau net. Justifier la réponse. (/1)
Comme l'oiseau est à 150 m, la distance OA est très grande devant la taille de l'œil et donc devant la distance OA'.
On peut donc faire l'approximation :
0
OA
1
Par conséquent,
f
1
OA'
1
La distance rétine-cristallin doit donc être égale à la distance focale.
La distance focale du cristallin sera donc de 17 mm lorsque le photographe voit l'oiseau net.

III - Aluminothermie [ / 6 ]
Une technique de soudure de rails de chemin de fer consiste à produire du fer en utilisant une transformation chimique. Cette technique est
appelée aluminothermie.
La réaction chimique qui a lieu lors de cette transformation fait intervenir côté réactifs un oxyde de fer Fe2O3 (s) et de l’aluminium Al (s). Les
produits de la réaction sont un oxyde d’aluminium Al2O3 (s) et le métal fer Fe (s).
1. Écrire l’équation de la réaction et l’équilibrer. (/1)
Fe2O3 (s) + 2 Al (s) → Al2O3 (s) + 2 Fe (s)
2. On dispose d’une quantité de matière d’oxyde de fer n0(Fe2O3) = 0,250 mol. Déterminer n0(Al) la quantité de matière d’aluminium
nécessaire pour que la réaction ait lieu dans les proportions stœchiométriques. Justifier la réponse. (/1)
Un mélange stœchiométrique est un mélange où les deux réactifs sont limitants car ils sont introduits dans les proportions où ils sont
consommés.
Ici, à chaque fois qu'on consomme un oxyde de fer, on consomme deux atomes d'aluminium. Par conséquent pour que le mélange soit
stœchiométrique, il faut que n0(Al) = 2 n0(Fe2O3)
AN : n0(Al) = 0,500 mol
3. Remplir le tableau d'avancement ci-dessous. (/2)
Avancement
(en mol )
Fe2O3 (s) + 2 Al (s) → Al2O3 (s) + 2 Fe (s)
État initial
0
0,250
0,500
0
0
État
intermédiaire
x
0,250 - x
0,500 - 2x
x
2x
État final
numérique
0,250
0
0
0,250
0,500
4. Calculer la masse de Fe qu'on s'attend à produire. (/1)
On s'attend à produire 0,500 mol de Fer.
m = n.M
AN : m = 0,500 × 55,85
m = 27,9 g
La masse de fer qu'on s'attend à obtenir est de 27,9 g.
5. On réalise l'expérience en laboratoire. Indiquer la démarche à suivre pour calculer le rendement de la réaction. (/1)
Par définition de rendement r est le rapport entre la masse de fer expérimentalement produite mexp et la masse de fer attendue
théoriquement qu'on vient de calculer, m.
Pour calculer le rendement, il faudrait donc isoler le fer produit, le peser puis calculer le rapport : r = mexp/m.
Données : M(Al) = 27,0 g.mol-1 ; M(Fe2O3) = 159,2 g.mol-1 ; M(Fe) = 55,85 g.mol-1 ; M(Al2O3) = 102 g.mol-1