Activité de modélisation : de l`usage des mathématiques en électricité

Activité de modélisation : de l’usage des mathématiques en électricité.
Objectif : utiliser des outils mathématiques pour résoudre des problèmes physiques
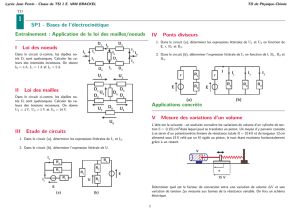
Problème n°1 : adaptation de résistance.
On considère un générateur de f.é.m E et de résistance interne r.
On va chercher à déterminer pour quelle valeur de la résistance R la puissance
transmise par le générateur sera maximale.
Questions
Critères de réussite
J’ai su
faire
Je n’ai
pas su
faire
1. Représenter le modèle équivalent du circuit.
Le générateur sera remplacé par son modèle
équivalent dans le circuit.
2. Déterminer l’intensité du courant dans le
circuit en fonction de E, r et R.
Le circuit sera simplifié avec la résistance
équivalente et on utilisera une égalité entre les
tensions.
3. Exprimer la puissance fournie par le
générateur en fonction de R, r et E.
Le bilan de puissance du circuit sera
correctement utilisé.
4. Quelle valeur de R en fonction de r rend
cette puissance maximale ?
La dérivée de la fonction P(R) par rapport à R
sera utilisée.
Problème n°2 : un tramway sur son chemin.
On représente un circuit de Tramway de la façon suivante, où
chaque résistance modélise la résistance électrique des lignes
d’alimentation du tramway.
Le générateur est supposé idéal avec une f.é.m E = 750 V. Le
moteur du tramway reçoit une puissance Pél =10 kW.
La résistance des lignes d’alimentation vaut 0,020 par km.
On cherche à prévoir la valeur de l’intensité dans le circuit
lorsque le tramway a parcouru 10 km, puis en fonction de la
distance d parcourue.
Questions
Critères de réussite
J’ai su
faire
Je n’ai
pas su
faire
1. Ecrire le bilan de puissance du circuit.
L’expression littérale prendra la forme d’une
égalité entre la puissance fournie et les
puissances reçues.
2. En déduire l’équation vérifiée par l’intensité
du courant lorsque le tramway est à 10 km du
générateur.
L’équation littérale sera écrite sous la forme
d’une équation du second degré.
3. Calculer la valeur de l’intensité.
L’équation sera résolue numériquement et une
seule valeur de l’intensité sera retenue en
argumentant.
4. Exprimer l’intensité en fonction de la
distance d parcourue par le tramway.
Une expression littérale sera donnée après une
discussion sur le discriminant de l’équation.
5. Comment varie cette intensité en fonction
de d ?
La fonction I(d) sera étudiée.
MG
R
R
+
-