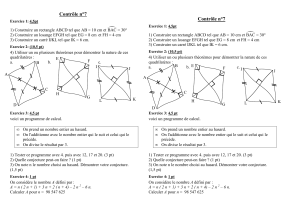
Chapitre 8 Le paralellogramme

Le parallelogramme
Pa1 Consigne :
A l'aide des outils proposés, construis le
quadrilatère ABCD
Explique ta construction
Le quadrilatère que tu as construit s'appelle un
Définition :
Un parallélogramme est un quadrilatère dont les
côtés sont
Pa2 Consigne La figure ci contre représente un
parallelogramme.
Mesure les différents segments, puis les angles du
quadrilatère ABCD. Fais bouger les points A,B …,
puis code la figure en fonction de tes observations.
Règles :
Dans un parallélogramme
 les côtés opposés ont
 les angles opposés ont
 les diagonales se
 le centre d'intersection des diagonales est
Pa3 Consigne : Construis le parallélogramme
ABCD.
Que représente le point O pour le quadrilatère
ABCD ?
Pourquoi ABCD est-il un parallélogramme ?
A et ….sont symétriques par rapport à …
… et …. sont aussi symétriques par rapport à O
Donc les segments [AB]. et . . . sont . . . . . . . . .
. . . . . .
Or deux segments symétriques par rapport à un
point sont p. . . . . . . . . .. . entre eux.
On en déquit que //
De même et pour les mêmes raisons, on obtient
[BC] //
ABCD a ses côtés opposés
donc ABCD est un
Règle :
Un quadrilatère non qui a ses diagonales
est un parallélogramme

Pa4 consigne : Construis le parallélogramme
ABCD.
Explique ta construction, puis code la figure.
En déplaçant les points A,B ou C, vérifie que ABCD
est bien un parallélogramme.
Dans quels cas ABCD n'est-il pas un
parallélogramme
Règle :
Un quadrilatère non croisé qui a
est un parallélogramme
Pa5 Consigne : Construis le parallélogramme
ABCD. Pourquoi esc-ce bien un parallélogramme
Règle :
Un quadrilatère non croisé qui a ses diagonales
est un parallélogramme
Pa6 Consigne
A l'aide des instruments de mesure proposés, que
peut-on dire des droites (AB) et (CD), puis des
segments [AB] et [CD]
Règle :
Un quadrilatère non croisé qui a deux côtés
est un parallélogramme
Pa7 Consigne
Construis les parallélogrammes RIEN, RIME et RAIE
si possible en utilisant trois méthodes différentes.

Le losange
L1 Consigne
A l'aide de l'outil compas, construire les points C et
D, pour que ABCD soit un parallélogramme. Le
point C doit être sur la demi droite.
Ensuite, dessine le parallélogramme obtenu.
La figure que tu as obtenue s'appellle un
Définition :
Un est un
qui a ses
Remarque :
Un losange est un
L2 La figure ci contre représente un losange.
En utilisant chacun des deux outils de construction
et de mesure proposés, cherche les propriétés des
diagonales puis, code la figure.
Règles :
Dans un losange
 les diagonales
 les diagonales sont
Démonstration du premier point:
B est equidistant de … et de … Donc B appartient à la
médiatrice du segment [ ]
De même, appartient aussi à la
du segment [ ]
Donc la droite ( ) est la de [AC]
La médiatrice d'un segment est à ce
segment. Donc
L3 Consigne
Construire le losange ABCD en utilisant tous les
outils proposés. La droite (d) est un axe de
symétrie.
Pour construire D j'utilise la symétrie par
rapport à
Pour construire C j'utilise la symétrie par
rapport à

L4 Consigne
ABCD est un parallélogramme. Que faut-il faire
pour le transformer en losange ?
Pourquoi est-ce un losange ?
Règle :
Un parallélogramme qui a
est un losange
L5 Consigne
ABCD est un parallélogramme. Que faut-il faire
pour le transformer en losange ?
Pourquoi est-ce un losange ?
Règle :
Un parallélogramme qui a
est un losange
L6 Consigne
Construire le losange ABCD. Le point B est sur la
droite (d)
Quelles propriétés du losange as-tu utilisé ?
L7 Défi 1
ABCD est un rectangle. Construire le losange AECF
de même périmètre que ABCD. Le point E est du
même côté que le point D par rapport à la droite
(AC)
L8 Défi 2
Construire le losange ABCD de centre O. Le point O
est sur la droite rouge, le point C est sur la droite
bleue et le côté [BC] est parallèle à la droite rouge

Le rectangle
R1 Consigne
A l'aide des outils disponibles, construire les points
C et D, pour que ABCD soit un parallélogramme. Le
point C doit être sur la droite.
La figure que tu as obtenue s'appelle un
Définition :
Un est un
qui a
Remarque :
Un rectangle est un
R2 La figure ci contre représente un rectangle.
En utilisant les outils de construction et de mesure
proposés, cherche les axes de symétrie de la
figure, et une propriétés des diagonales
Règles :
Dans un rectangle
 les diagonales ont
 les axes de symétrie sont
R3 – Consigne
ABCD est un parallélogramme. Que faut-il faire
pour le transformer en rectangle ?
Pourquoi est-ce un rectangle?
Règle :
Un parallélogramme qui a
est un rectangle
R4 Consigne
ABCD est un parallélogramme. Que faut-ik faire
pour le transformer en rectangle ?
Pourquoi est-ce un rectangle?
Règle :
Un parallélogramme qui a
est un rectangle