EXERCICE II Un service au tennis (5,5 points)

Mise en situation : un service au tennis
Objectif : identifier les raisonnements à savoir mettre en oeuvre concernant la chute libre d’un projectile.
Un terrain de tennis est un rectangle de
longueur 23,8 m et de largeur 8,23 m. Il
est séparé en deux dans le sens de la
largeur par un filet dont la hauteur est
0,920 m.
Lorsqu’un joueur effectue un service, il
doit envoyer la balle dans une zone
comprise entre le filet et une ligne située à
6,40 m du filet.
On étudie un service du joueur placé au
point O.
1. Lancer vertical de la balle.
Le joueur lance verticalement la balle d’un point A situé à une hauteur h = 1,80 m à un instant pris
comme origine des dates avec une vitesse initiale
v0
verticale orientée vers le haut. Avant de
redescendre, la balle atteint un point D situé à la hauteur H = 2,20 m par rapport à l’origine des
altitudes prise au niveau du sol.
La masse de la balle est de 53,0 g et son rayon vaut r = 3,0 cm.
On rappelle que la masse volumique de l’air vaut 1,3 g.dm-3 à 20°C.
2. Mouvement de la balle après la frappe.
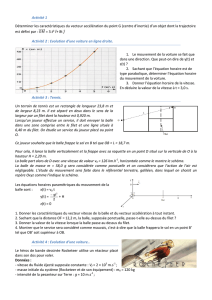
Ce joueur souhaite que la balle frappe le sol en B tel que OB = L = 18,7 m.
Pour cela, il lance la balle verticalement et la frappe avec sa raquette en un point D situé sur la verticale de O à
la hauteur H = 2,20 m.
Dans cette nouvelle phase du mouvement, la balle part alors de D à un instant pris comme nouvelle origine des
dates avec une nouvelle vitesse initiale de valeur v0 = 126 km.h-1, horizontale comme le montre le schéma ci-
dessous.
La balle de masse m = 58,0 g sera considérée comme ponctuelle et on considérera que l’action de l’air est
négligeable.
L’étude du mouvement
sera faite dans le
référentiel terrestre,
galiléen, dans lequel on
choisit un repère Oxyz
comme l’indique le
schéma ci-contre :
1.1. Faire le bilan des forces susceptibles d’être appliquées à la balle pendant
son mouvement vertical.
En indiquer les caractéristiques (direction, sens, grandeur) et l’expression.
Les forces seront représentées de façon
cohérente sur un schéma.
1.2. Montrer que la poussée d’Archimède de l’air sur la balle est négligeable.
Vous montrerez que la poussée
d’Archimède est au moins 100 fois
inférieure au poids.
1.3. On néglige les frottements de l’air dans cette phase du mouvement de la
balle. Établir l’expression du vecteur accélération de la balle au cours de son
mouvement.
La 2e loi de Newton sera correctement
appliquée.
1.4. Ecrire littéralement l’équation horaire du mouvement vertical de la balle.
L’axe des altitudes sera pris orienté vers le haut.
Les conditions initiales seront bien
prises en compte.
1.5. En déduire la valeur de la vitesse de la balle nécessaire pour atteindre cette
hauteur.
La vitesse initiale sera calculée à partir
de l’équation horaire prise à l’instant où
la vitesse s’annule.
B
O
L
Filet
0
v
i
k
j
O
z
y
D
F
Filet
B
x
y
O
A
v0
uru
A
D

2. Équations horaires paramétriques et trajectoire.
2.1. Établir l’expression du vecteur accélération de la balle au cours de son
mouvement en négligeant l’action de l’air sur la balle.
Une expression vectorielle sera
écrite à partir de la 2e loi de
Newton.
2.2. Montrer que les équations horaires paramétriques du mouvement de la
balle sont :
x(t) = v0 t y(t) =
2 gt
2
+ H z(t) = 0
Les coordonnées de l’accélération
puis du vecteur vitesse et du
vecteur position seront déduites
successivement.
2.3. Montrer que le mouvement de la balle a lieu dans un plan.
L’une des équations horaires sera
correctement exploitée.
2.4. Déduire de la réponse à la question 2.3. l’équation littérale de la
trajectoire de la balle dans le plan xOy.
L’instant t sera exprimé en
fonction de x.
3. Qualité du service.
On prendra g = 9,81 m.s-2.
3.1. Sachant que la distance OF = 12,2 m, la balle, supposée ponctuelle,
passe-t-elle au-dessus du filet ?
L’équation de la trajectoire sera
utilisée à la bonne position
horizontale.
3.2. Montrer que le service sera considéré comme mauvais, c’est-à-dire que
la balle frappera le sol en un point B’ tel que OB’ soit supérieur à OB.
L’équation de la trajectoire sera
utilisée à la bonne position
verticale.
3.3. En réalité, la balle tombe en B. Quel est le paramètre, non pris en compte
dans ce problème, qui peut expliquer cette différence ?
Une des hypothèses de l’énoncé
sera discutée.