La mesure du temps dans l`histoire de la Terre et de la vie

RR - 16/04/17 - 769783889 - 1/8
La mesure du temps
dans l’histoire de la Terre et
de la vie
► TP 1. La datation relative
I. La datation relative repose sur quatre principes
A. Le principe de superposition s'applique aux successions de couches ordonnées
B. Le principe de recoupement s'applique aux situations d'intersection
C. Le principe de continuité s'applique aux couches dispersées
D. Le principe d'identité paléontologique permet d'étendre le marqueur temporel quand le principe de
continuité n'est pas applicable
II. La datation absolue repose essentiellement sur la radiochronologie
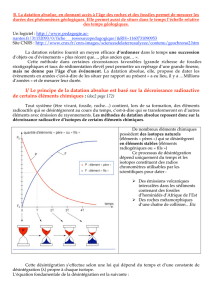
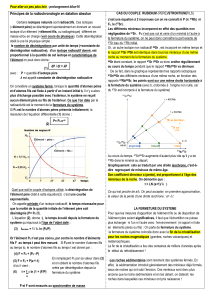
A. La radiochronologie est fondée sur la décroissance radioactive de certains éléments chimiques
B. Les radiochronomètres sont choisis en fonction de la nature et de l'âge présumé de l’échantillon
►TP 2. La datation absolue
OBJECTIF
► FIGURE 1. Les grands traits de l'histoire de la terre dans Nathan p. 154.
► QUESTION. Comment a-t-on obtenu ces dates ?
 Pour mesurer des temps courts (de la fraction de seconde à quelques
années) on dispose d'appareils (ex. : horloges, chronomètres). Les
calendriers permettent de nous situer dans les temps historiques
(5 000 ans environ).
 Le géologue, qui raisonne sur des durées allant jusqu'au milliard
d'années, utilise d'autres outils : la datation relative et la datation
absolue.
 On cherche à préciser les fondements et le mode d'utilisation de ces
deux méthodes.
 Actualisme (Lyell, 1830) . "Les lois régissant les phénomènes géologiques actuels
étaient également valables dans le passé".
Ce chapitre peut être indépendant ou être intégré à d'autres chapitres. Il est
suggéré d'illustrer les méthodes de chronologie relative et absolue à partir
d'exemples choisis dans les chapitres "convergence (subduction, collision)",
"parenté entre êtres vivants actuels et fossiles-phylogenèse-évolution".
Ce chapitre est ici placé en dernier chapitre de géologie (comme une conclusion
au regard de l'introduction sur le temps). Cela permet d'intégrer toutes les
connaissances de l'année (en SVT, Maths et PC).
► TP 1. La datation relative
Termle S
Chapitre
5.1
2 semaines

RR - 16/04/17 - 769783889 - 2/8
I. La datation relative repose sur quatre principes
 La datation relative (= chronologie relative) permet d'ordonner les uns par
rapport aux autres les objets et les événements géologiques et biologiques (sans
référence à des nombres d'années).
Quelques objets et événements géologiques que l’on peut dater par datation relative
(liste non exhaustive).
- Strate (= couche, banc, lit, niveau) : ensemble sédimentaire ou volcanique compris
entre deux surfaces approximativement parallèles correspondant à une discontinuité
avec les terrains voisins.
- Pli : déformation résultant de la flexion ou de la torsion de roches.
- Faille : cassure de terrain avec déplacement relatif des parties séparées (normale,
inverse, décrochement).
- Discordance : interruption stratigraphique résultant généralement d'une phase
d'érosion comprise entre une phase de sédimentation et les dépôts et remaniements
antérieurs. Il y a interruption de la continuité de dépôt.
- Sédimentation : ensemble des processus permettant, en milieu aquatique, le dépôt de
particules plus ou moins grosses ou de matières précipitées.
- Intrusion : roche qui pénètre dans des formations déjà constituées et qui les recoupe.
- Orogenèse : processus conduisant à la formation d'une chaîne de montagnes.
► FIGURE 2. Le principe de superposition dans Nathan p. 156 (même
document dans Bordas p. 242 où il est resitué dans les Alpes).
A. Le principe de superposition s'applique aux successions de couches
ordonnées
 Quand deux couches (sédimentaires ou volcaniques) sont superposées, celle du
dessous est le plus ancienne que celle du dessus.
C'est une conséquence de leur mise en place en couches successives.
 Ce principe ne s'applique pas :
- aux couches qui ont subi des déformations intenses pouvant conduire à une inversion
de l'ordre de mise en place ;
- aux roches métamorphiques ou aux filons magmatiques car leur mode de mise en
place ne correspond pas à un dépôt.
B. Le principe de recoupement s'applique aux situations d'intersection
 Lorsque deux objets géologiques se recoupent, celui qui recoupe l'autre est le
plus récent.
► FIGURE 3a. Pli et faille dans Nathan p. 216.
 Cela est vrai à l'échelle du paysage :
- une faille, un pli ou une intrusion magmatique sont plus récents que la
formation qu'ils affectent ;
► FIGURE 3b. Une discordance dans Nathan p. 157. Voir définition ci-dessus.
- une discordance a un âge encadré entre celui de la dernière couche située au
dessous et celui de la première couche située au dessus.
► FIGURE 3c. Détail de la granodiorite d’Athis dans Nathan p. 161.
 Cela est vrai à l'échelle de l'échantillon : des galets inclus dans une roche
détritique sont antérieurs à cette roche.
► FIGURE 3d. Métagabbro à glaucophane d’après Bordas p. 222 et 223. La
glaucophane se forme à l’interface plagioclase pyroxène.
 Cela est vrai à l'échelle des minéraux :
- quand un minéral est inclus dans un autre, il lui est antérieur ;

RR - 16/04/17 - 769783889 - 3/8
- un minéral qui recoupe un autre a cristallisé en dernier ;
- l'apparition d'un minéral caractéristique d'une réaction métamorphique le situe par
rapport aux minéraux préexistants.
 Une roche métamorphique peut renfermer des minéraux qui ne sont pas
complètement transformés. Les réactions se produisant de l'extérieur vers l'intérieur du
minéral, le minéral présent au départ sera alors inclus au sein d'une couronne du nouveau
minéral.
► FIGURE 4. Le principe de continuité : extension des calcaires urgoniens dans
Nathan p. 158.
C. Le principe de continuité s'applique aux couches dispersées
 Une même couche est de même âge en tous points, même si elle est dispersée.
La dispersion est généralement liée à des accidents de terrain ultérieurs au dépôt de la
couche.
 Des couches séparées dans l'espace, mais limitées par les mêmes couches à la
base et au sommet, sont de même âge. Cela est vrai même si ces couches ne sont
pas de même nature, car les conditions de sédimentation varient d'un endroit à
l'autre. Ce principe ne s'applique pas à une couche transgressive (avancée de la mer sur un
continent) où les dépôts sont de plus en plus jeunes au fur et à mesure de la progression
du phénomène.
► FIGURE 5. Le principe d'identité paléontologique dans Nathan p. 159.
VOIR. Bordas p. 167 à 169.
D. Le principe d'identité paléontologique permet d'étendre le marqueur
temporel quand le principe de continuité n'est pas applicable
 Deux strates contenant la même association de fossiles (fossiles stratigraphiques)
ont le même âge.
 On appelle fossile stratigraphique une espèce abondante, ayant une grande
extension géographique et une existence courte à l'échelle géologique (ex. / beaucoup de
Foraminifères, les Ammonites…). On l'oppose à un fossile de faciès qui est lié à un
milieu de sédimentation particulier (ex. : Oursins).
 Cette méthode (la biostratigraphie) n'est applicable qu'aux roches sédimentaires
contenant des fossiles (donc d'âge inférieur à 540 Ma).
II. La datation absolue repose essentiellement sur la
radiochronologie
 La datation absolue (= chronologie absolue), permet de donner un âge en années
aux roches et aux fossiles. On peut ainsi mesurer la durée des phénomènes
géologiques.

RR - 16/04/17 - 769783889 - 4/8
A. La radiochronologie est fondée sur la décroissance radioactive de
certains éléments chimiques
Accompagnement. Le développement mathématique et physique permettant
d'aboutir à la détermination de l'âge d'une roche ne peut pas faire l'objet d'une
question au baccalauréat dans l'épreuve de SVT. Il est ici fourni à titre
d’information.
L'élève doit savoir exploiter un document ou des données numériques sur les
rapports isotopiques en relation avec le calcul de l'âge absolu des roches ; dans le
cas où des formules mathématiques sont nécessaires, celles-ci sont fournies.
►FIGURE 6a. Décroissance radioactive dans Bordas p. 172.
►FIGURE 6b. Principes de radiochronologie
►FIGURE 6c = POLYCOPIE. Principes de radiochronologie voir aussi Nathan
p. 164 fig. 1, Didier p. 214, Caron p. 209.
 Un isotope "père" P (= radiogène = radioactif), se désintègre spontanément en
un isotope "fils" F (= radiogénique), selon une fonction exponentielle du temps
(cf. cours de physique et de mathématiques) :
P = P0 e-
t donc
P
P
ln
1
t0
λ
[1]
avec
P = quantité d'isotope père actuelle
P0 = quantité d'isotope père initiale
F = quantité d'isotope fils actuelle
F0 = quantité d'isotope fils initiale
= constante de désintégration (= probabilité de désintégration par unité de temps, valeur propre
à chaque isotope radioactif)
t = durée de désintégration
Démonstration
La quantité d'atomes radioactif dP disparaissant par désintégration pendant un intervalle de temps
dt est telle que dP/dt = - P0
Si on intègre cette expression on obtient : P = P0 e-
t
De cette équation on tire P0 / P = 1 / e-
t = e t d'où
t = ln P0 / P (ln = logarithme népérien).
Donc t = 1/ . ln P0 / P
 La désintégration nucléaire s'accompagne de l'émission de particules (noyaux
d'He), (électrons) ou d'énergie (rayonnement ).
 La désintégration nucléaire n'est pas l'aboutissement d'un processus de vieillissement
du noyau. Un noyau se désintègre sans avoir "vieilli".
 On appelle période T (= demi-vie) le temps nécessaire pour diminuer de moitié
une quantité quelconque d'élément père.
T et sont liés par la relation T = 0,693 /
Démonstration
D'après [1] PT = P0 / 2 = P0 e-
T on a donc 1/2 = e-T et 2 = eT
Ainsi T = ln 2 = 0,693 et T= ln 2/ donc T = 0,693 /
 En général P0 est inconnu mais F est mesurable. On a alors
F = F0 + P. t donc
λ P FF
t0
[2]
Démonstration
La quantité F d'isotope fils actuelle est égale à la quantité initiale F0 plus la quantité formée par
désintégration Fd, soit : F = F0 +Fd. Or Fd est égal à la quantité d'isotope père désintégré (un
atome de P donne un atome de Fd), on a donc Fd = P0 - P d'où : F = F0 + (P0 - P)
Puisque d'après [1] P0 = P e
t on peut écrire F = F0 + ( P e t - P) soit F = F0 + P (e t - 1)
- Or e
t -1
t cette approximation est très pratique et on peut à tout moment revenir à
l'expression initiale.
On a donc F = F0 + P. t et t = F - F0 / P
- On peut aussi choisir de "traîner" e
t -1.
Puisque F = Fo + P (e
t - 1) on a F - F0 = Pe t - P donc F-F0 / P = e t - 1 et F - F0 + 1 = e t d'où on
tire t = 1/ ln (F - F0 / P + 1).

RR - 16/04/17 - 769783889 - 5/8
 La radiochronologie mesure la variation du rapport isotopique entre le moment
de la fermeture de l'échantillon daté et le présent (t). On appelle "fermeture" du
système le moment où plus aucun constituant n'a pu ni entrer ni sortir de
l'échantillon. Les éléments chimiques évoluent alors spontanément et les
quantités d'éléments pères diminuent selon leur demi-vie.
 Les roches sédimentaires ne sont jamais des systèmes fermés, la
radiochronologie ne permet pas de les dater, sauf avec le 14C. Pour les roches
magmatiques et métamorphiques la fermeture du système correspond à la
cristallisation complète c'est à dire à la fin du refroidissement.
Pour les roches grenues (métamorphiques et plutoniques) cette cristallisation ne
s'achève que plusieurs centaines de milliers d'années, parfois même plusieurs millions
d'années, après la mise en place. La cristallisation est beaucoup plus rapide pour les
roches volcaniques (elle est "immédiate" à l'échelle géologique).
► FIGURE 7. Des géochronomètres adaptés à leur utilisation dans Nathan p.
169.
B. Les radiochronomètres sont choisis en fonction de la nature et de
l'âge présumé de l’échantillon
 La datation radiochronologique n'est valide que si l'on mesure des durées allant
du centième à dix fois la période T de l'isotope choisi (au delà les mesures des
quantités d'isotopes ne sont pas fiables).
► FIGURE 8. Le géochronomètre 14C dans Nathan p. 176
1. Le carbone 14 pour les derniers millénaires
 Le C est très abondant dans les matières organiques, les roches carbonatées et les
roches carbonées. Il possède deux isotopes stables 12C (le plus courant) et 13C
plus un isotope radioactif naturel 14C qui se désintègre en 14N.
T du 14C = 5 730 ans et = 1,209. 10-4. an-1
La datation est fiable jusqu'à 50 000 ans (30 000 à 40 000 ans de préférence).
 Le 14C est produit régulièrement dans la haute atmosphère (en quantité égale à
la désintégration). Il s'oxyde ensuite en 14CO2 et participe au cycle du carbone
(cf. cours de 2e chapitre 1.3-II) avant de se désintégrer.
14N est transformé en 14C sous l'effet neutrons cosmiques, on a : 14N + n  14C + p.
Quand 14C se désintègre il redonne 14N.
Le 14C est donc en proportion constante dans tous les réservoirs :
14C / 12C = 1,2 . 10-12 = constante
 La fermeture du système au carbone est opérée quand un organisme meurt,
qu'un carbonate est précipité et isolé ou qu’une masse d'eau est isolée. Ils
cessent alors d'incorporer du carbone. Dans l'échantillon la quantité de 14C
diminue en fonction du temps et la mesure de la quantité de 14C résiduelle permet
de calculer la date de fermeture.
 Puisque P0 est connu, l'expression [1] peut être directement utilisée
14C = 14C0 e- t donc
C
C
ln
1
t14
0
14
λ
Puisque la quantité de 12C est constante (ni radioactif ni radiogénique), on peut aussi écrire :
14C / 12C = (14C / 12C) 0 . e- t d’où on tire t = 1 /
. ln 14C0/ 12C
 Le rapport 14C/12C a en fait varié dans le temps. Par exemple l'âge
radiochronologique d'arbres fossiles est inférieur à leur "âge vrai" mesuré par