109-Spectre de H

Encadrement - Le spectre de l'hydrogène atomique
1
Le spectre de l’hydrogène atomique
Objectif général :
Observer le spectre d’émission de l’hydrogène atomique et déterminer des grandeurs
physiques reliées au modèle atomique de Bohr.
Objectifs spécifiques :
Effectuer des mesures sur un spectroscope.
Effectuer des calculs à l’aide de l’équation de Bohr.
Établir des liens entre le spectre de l’hydrogène et la théorie atomique de Bohr.
Identifier les couches électroniques responsables des raies observées.
Calculer l'énergie des couches électroniques identifiées.
la théorie
On sait depuis le début du siècle qu'un électron dans un atome possède une énergie
potentielle dont la valeur dépend de la couche électronique sur laquelle il se trouve. L'électron
ne peut donc posséder que certaines valeurs d'énergie potentielle, à savoir celles qui sont
caractéristiques de ces couches, mais jamais de valeur intermédiaire. Ces couches sont aussi
appelées, pour cette raison, niveaux d'énergie. Cette caractéristique des électrons de ne
pouvoir posséder que certaines valeurs permises d'énergie signifie que l'énergie de l'électron
est quantifiée. Ce postulat a donné naissance, dans les années 20, à la théorie quantique.
Cette théorie prévoit entre autres l'existence de paramètres appelés nombres
quantiques. Dans un atome hydrogénoïde, c'est-à-dire ne comportant qu'un seul électron
(comme l'atome d'hydrogène), l'énergie potentielle ne dépend que d'un seul nombre quantique,
le nombre quantique principal n. La figure 1 illustre les niveaux d'énergie dans un tel atome.
Cette figure montre que le nombre quantique principal n est toujours un nombre entier
et qu'il varie de 1 à l'infini. Il montre aussi que le niveau n = 1 correspond à la plus basse

Expérience 7 - Le spectre de l'hydrogène atomique
2
énergie potentielle que peut posséder un électron dans un atome. Enfin, remarquons que plus
n augmente, plus la différence d'énergie entre deux niveaux voisins est réduite.
n = ∞
n = 4
n = 3
n = 2
n = 1
Figure 1 : Énergie potentielle selon le nombre quantique principal n
dans un atome hydrogénoïde
Il est possible pour un électron de passer d'un niveau d'énergie à un autre dans un
atome donné. Comme chaque niveau possède sa propre valeur d'énergie potentielle, ce
passage d'un niveau à un autre est toujours accompagné d'une variation d'énergie. Ainsi,
lorsqu'un électron quitte son niveau pour aller à un niveau plus bas (i.e. où n est plus petit),
son énergie potentielle diminue ; l'énergie perdue est alors émise sous forme de radiation
électromagnétique, c'est-à-dire qu'un photon est émis. Inversement, il faut fournir de l'énergie
à un électron pour qu'il puisse passer de son niveau d'énergie à un niveau supérieur (où n est
plus élevé).
À l'état fondamental, l'ensemble des électrons possède la plus basse énergie
potentielle possible. En fournissant de l'énergie à un atome, on peut faire passer des électrons
à des niveaux plus élevés ; l'atome est alors dans un état qu'on appelle excité. Cet état n'est pas
stable : les électrons reviennent rapidement à leur niveau initial, en émettant des radiations
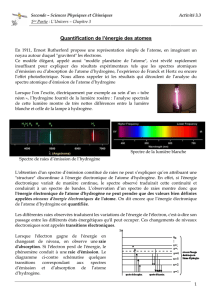
électromagnétiques. Lorsqu’on décompose à l’aide d’un prisme la lumière émise par un
élément excité, on obtient ce qu’on appelle un spectre de raies (cf. figure 2). Celui-ci est
caractéristique de chaque élément puisque chaque raie correspond à la différence d’énergie
entre deux couches électroniques. Il est essentiel de comprendre ce dernier point : une raie ne
correspond pas à un niveau d'énergie, mais à la différence d'énergie entre deux niveaux.

Encadrement - Le spectre de l'hydrogène atomique
3
Couleur de la raie : rouge turquoise bleue violette
Figure 2 : Spectre de raies de l'hydrogène
Les niveaux d’énergie d’un élément donné lui sont particuliers puisque l’énergie d’un
niveau dépend de la charge du noyau, du nombre d’électrons, de la distance entre les
électrons, etc. Chaque élément possède donc ses propres niveaux d’énergie, d’où ses propres
transitions électroniques, d’où son propre spectre de raies. Celui-ci constitue donc «
l’empreinte digitale » d’un élément. On a pu, par exemple, détecter la présence d’hélium sur
le soleil (en 1868) avant qu’il ne soit découvert sur Terre (en 1895). (Le mot hélium vient du
grec helios, qui signifie soleil.)
Un spectre de raies nous renseigne aussi sur l’énergie des niveaux. Comme chaque raie
correspond à une certaine longueur d’onde (d'où sa couleur caractéristique), on peut calculer
la variation d’énergie qui lui est associée par la relation :
∆E =
Error!
(1)
où : ∆E : variation d’énergie (J)
h : constante de Planck (6,626 x 10-34 J·s)
c : vitesse de la lumière (2,9979 x 108 m/s)
 : longueur d’onde (m)
La variation d’énergie ainsi calculée est la différence d’énergie entre deux niveaux. On

Expérience 7 - Le spectre de l'hydrogène atomique
4
trouve l’énergie d’un niveau en déterminant à quelles transitions correspondent les raies
observées et en posant que le niveau n = ∞ possède une énergie potentielle de 0.
Pour un atome monoélectronique tel que l’atome d'hydrogène, on peut se servir de
l’équation obtenue par Bohr à partir de son modèle atomique :
E = -2,178 x 10-18 (
Error!
) J
(2)
où : E : énergie d’un niveau (J)
Z : numéro atomique (1 pour l’hydrogène)
n : niveau d’énergie (i.e. nombre quantique principal)
On a donc pour l’hydrogène :
E = - 2
178 x 10-18;n2 J (3)
Pour une transition électronique d’un niveau supérieur ni à un niveau inférieur nf, on
obtient :
∆E = Eni - Enf = -2
178 x 10-18;ni2 - -2 178 x 10-18;nf2
∆E = -2,178 x 10-18 (
Error!
-
Error!
)
∆E = 2,178 x 10-18 (
Error!
-
Error!
)
(4)
(Note : on écrit ni et nf pour représenter, respectivement, n initial et n final.)
L'ensemble des raies visibles du spectre de l’hydrogène constitue ce qu'on appelle la
série de Balmer. Elles sont caractérisées par le fait que, dans chaque transition, le niveau infé-
rieur (nf) est 2 :
∆E = 2,178 x 10-18 (
Error!
-
Error!
)
(5)

Encadrement - Le spectre de l'hydrogène atomique
5
Comme ∆E est relié à la longueur d’onde de la raie observée (cf. équation 1), on peut
écrire :
Error!
= 2,178 x 10-18 (
Error!
-
Error!
)
(6)
Cette dernière équation permettra de déterminer, pour chaque raie observée au labora-
toire, le niveau supérieur (ni) de la transition correspondante, puisque l'expérience réalisée
permettra de déterminer  pour chaque raie et que h et c sont des valeurs connues. Il faut se
rappeler, en utilisant cette équation, que ni est un nombre entier ; il faudra donc arrondir à
l'entier le plus près le résultat du calcul.
La détermination de l’énergie d’un niveau ni est plus difficile puisque, comme on l’a
mentionné plus haut, une raie dans un spectre correspond à une différence d’énergie entre
deux niveaux et non pas à l’énergie d’un niveau. Il faudra donc, dans cette expérience, poser
une valeur d’énergie pour le niveau n = 2 (le niveau inférieur de chaque transition) et calculer
l’énergie du niveau supérieur de chaque transition. En effet, ∆E peut être calculé par
l’équation 1 :
∆E =
Error!
et correspond à :
∆E = Eni - E2 (7)
Si on pose, provisoirement, que l’énergie du niveau 2 est de 0, on aura :
∆E = E*;ni - 0
Error!
= E
Error!
(8)
où E*;ni est l’énergie « provisoire » du niveau supérieur de chaque transition observée.
(Rappelons que la convention est d'assigner une valeur d'énergie de 0 au niveau n = ∞.)
La valeur réelle de l’énergie d’un niveau ni pourra être déterminée à l’aide d’un gra-
phique de E*;ni en fonction de 1/ni2 (voir figure 3). Ce graphique donne une droite puisque,
comme on l’a vu à l’équation 3, l’énergie d’un niveau est inversement proportionnelle au