Chapitre 22

MPSI Chapitre 22
GAZ PARFAITS, PRESSION ET TEMPÉRATURE CINÉTIQUES
22-1 Propriétés thermoélastiques des gaz parfaits
22-1-1 Loi de Boyle et Mariotte
Il s'agit d'une loi approchée, que les gaz suivent d'autant mieux que leur pression est plus faible et leur
température plus élevée.
Loi de Boyle et Mariotte : pour un gaz donné à T et n constants pV = Cte .
22-1-2 Gaz parfait
À chaque gaz réel on peut associer un gaz parfait dont les molécules seraient les mêmes et dont le
produit pV à température constante aurait, pour une quantité de gaz donnée, la même valeur que pour le gaz
réel considéré sous une pression tendant vers zéro.
Pour un gaz parfait donné, avec T et n constants,
réel
0p pVlimpVp
Donc les gaz parfaits suivent exactement 1a loi de Boyle et Mariotte
La température absolue est proportionnelle par définition la limite du produit pV pour p tendant vers
zéro. Un gaz parfait suit donc par définition la loi suivante :
Loi des gaz parfaits : Pour un gaz parfait associé à un gaz réel donné, à n constant
te
C
T
pV 
.
Cette constante dépend à priori de la nature chimique du gaz réel associé au gaz parfait et de la
quantité de matière de ce gaz considérée.
Le produit pV étant une grandeur extensive, de même que la masse et la quantité de matière, il est
donc proportionnel à la masse et à la quantité de matière.
La loi des gaz parfaits peut donc s'écrire pV = nRT, n étant la quantité de matière en molécules du
gaz (soit pVm = RT). R dépendant à priori uniquement de la nature chimique du gaz.
On pourrait tout aussi bien l'écrire pour le moment pV = m K T, m étant la masse du gaz, (soit, avec
, masse volumique, p = KT). K dépendant à priori uniquement de la nature chimique du gaz.
22-1-3 Loi d'Avogadro et Ampère
Le choix de la variable quantité de matière se justifie par la loi d'Avogadro et Ampère qui justement
affirme que R ne dépend pas de la nature chimique du gaz parfait considéré.
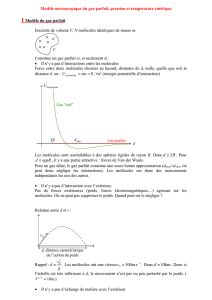
En effet, si on compare les isothermes en coordonnées d'Amagat pour différents gaz et pour une
même température, on constate expérimentalement qu'extrapolées à p = 0 elles passent toutes par le même
point A.
CO2
H2
O2
pVm
/ (J.mol1)
p / bar
1.103
2.103
105
gaz parfaits
Isothermes à 0 °C
A
CO2
H2
O2
pVm
/ (J.mol1)
p / bar
1.103
2.103
105
gaz parfaits
Isothermes à 0 °C
A

On voit d'après ces isothermes que, pour p tendant vers zéro, les produits pVm sont les mêmes, et par
conséquent les volumes sont les mêmes pour des quantités de matière égales de gaz différents, à la même
température.
La loi d'Avogadro et Ampère est une loi approchée pour les gaz réels. Elle s'énonce ainsi :
Loi d'Avogadro et Ampère : À température donnée, sous une pression donnée, des volumes égaux
de gaz différents, contiennent la même quantité de matière en molécules de gaz.
Pour un gaz qui suit la loi d'Avogadro et Ampère, le volume molaire ne dépend donc que de T et p; il
est indépendant de la nature du gaz.
Elle n'est vérifiée pour les gaz réels que pour p tendant vers zéro.
Pour les gaz parfaits, les isothermes pVm = f(p) sont des droites horizontales donc pVm = A(T) pour
toute pression. Un gaz parfait suit exactement la loi d'Avogadro et Ampère.
22-1-4 Équation d'état des gaz parfaits, constante des gaz parfaits
Pour un gaz parfait, pV = nRT (ou pVm = RT) et pour T fixée, pVm ne dépend pas de la nature du
gaz. Donc R est une constante universelle. C'est-à-dire que cette constante ne dépend pas de la nature du gaz
réel auquel est associé le gaz parfait considéré. On la nomme constante des gaz parfaits.
Sa valeur est donnée par extrapolation à pression nulle sur une isotherme d'un gaz réel quelconque en
coordonnées d'Amagat: Constante des gaz parfaits :
réel
m
0p pVlim
T
1
R
.
Son unité SI est Pa.m3.mol–1.K–1 = N.m–2.m3.mol–1.K–1 = J.K–1.mol–1.
Sa valeur est :
11 mol.K.J31441,8R 
.
L'équation d'état d'un gaz parfait est donc
nRTpV 
soit encore
RTpVm
.
On pourra retenir les valeurs suivantes :
Conditions normales de température et de pression : p0 = 101325 Pa , T0 = 273,15 K .
Volume molaire normal des gaz parfaits :
1133
0
0
0m mol.L4,22mol.m10.414,22
p
RT
V 
. (Ces
trois chiffres sont largement suffisants puisque aucun gaz réel n'est parfait dans les conditions normales).
22-1-5 Coefficients thermoélastiques des gaz parfaits
De l'équation d'état pVm = RT, on peut déduire
T
dT
V
dV
p
dp
m
m
en utilisant les différentielles
logarithmiques. Donc:
à p constante
T
1
dT
dV
V
1m
m
soit encore :
T
1
T
V
V
1
p
m
m
,
à T constante
p
1
dp
dV
V
1m
m
soit encore :
p
1
p
V
V
1
T
m
m
T
.
22-1-6 Lois de Gay-Lussac et de Charles
L'équation d'état des gaz parfaits pV = nRT implique que tous les gaz parfaits obéissent aux lois
suivantes :
Si n et T sont constantes, alors
te
CpV 
: loi de Boyle et Mariotte.
Si p et T sont constantes, alors
te
mCV
n
V
: loi d'Avogadro et Ampère.
Si p et n sont constantes, alors
te
C
T
V
: loi de Gay-Lussac.
Si V et n sont constantes, alors
te
C
T
p
: loi de Charles.
On peut démontrer que tout gaz qui obéit à la fois aux lois de Gay-Lussac et de Charles est un gaz
parfait.

21-1-7 Masse volumique et densité d'un gaz parfait
La masse volumique d'un gaz parfait est
RT
Mp
V
M
V
m
m
(M étant la masse molaire,
éventuellement la masse molaire moyenne s'il s'agit d'un mélange de gaz).
La connaissance de la masse volumique dans les conditions normales de température et de pression
permet donc de calculer la masse volumique dans n'importe quelles conditions où le gaz peut être considéré
comme parfait, si l'on peut assimiler le gaz à un gaz parfait dans les conditions normales :
0
0
0RT
Mp
donc
Tp
pT
0
0
0
.
Par exemple pour l'air, dont la composition est pratiquement uniforme, la masse molaire moyenne est
MA = 28,98.10–3 kg.mol–1. Dans les conditions normales, c'est pratiquement un gaz parfait (mélange idéal de
gaz parfaits), sa masse volumique est :
0
0A
0
ARTpM
= 1,293 kg.m–3.
Pour p et T donnés, le rapport de la masse volumique d'un gaz à celle de l'air est la densité du gaz
(sous entendu : par rapport à l'air).
Densité d'un gaz :
A
d
.
Si le gaz et l'air peuvent être considérés comme parfaits à T et p considérés
1
Amol.g29 M
M
M
d
.
22-2 Mélanges de gaz parfaits
22-2-1 Expérience de Berthollet. Notion de mélange idéal
Deux échantillons de gaz identiques à la même pression (équilibre mécanique) et à la même
température (équilibre thermique) se mélangent avec addition de leurs volumes (grandeur extensive) sans
qu'il y ait de variation de leur température ni de leur pression (grandeurs intensives).
Si les gaz sont différents il n'en est pas toujours de même.
L'expérience de Berthollet consiste à mettre en communication deux récipients contenant des gaz
différents à la même température et à la même pression, en ouvrant le robinet qui les séparait. L'ensemble
étant placé dans une enceinte adiabatique et indéformable (pour éviter tout échange avec l'extérieur).
Au bout d'un temps plus ou moins long, les deux gaz sont intimement mélangés grâce au phénomène
de diffusion lié à l'agitation thermique. Des manomètres reliés aux récipients permettent le plus souvent de
ne constater aucune variation de pression notable. C'est le cas par exemple si l'on mélange O2 et CO2 ou H2
et N2... Si la variation de pression est exactement nulle, on dit que le mélange est idéal.
22-2-2 Conditions d'idéalité d'un mélange de gaz parfaits
I1 ne suffit pas que deux gaz soient parfaits pour que leur mélange soit idéal. En effet. si l'on mélange
deux gaz parfaits tels que O2 et NO qui réagissent entre eux suivant 2 NO + O2 = 2 NO2 dans des
conditions de température et de pression telles que ces trois gaz puissent être considérés comme parfaits,
après retour à la température initiale, la pression aura été réduite aux 2/3 de sa valeur initiale comme la
quantité de matière en molécules de gaz.
La non idéalité d'un mélange de gaz est donc liée aux interactions entre les molécules des gaz
mélangés. Même si celles-ci ne vont pas jusqu' à une réaction chimique caractérisée, il suffira que des forces
d'interaction électrostatiques entre les molécules différentes ne soient pas de même intensité que celles entre
molécules identiques pour que le mélange ne soit pas idéal.
Supposons maintenant que l'on réalise l'expérience de Berthollet avec des gaz parfaits ne réagissant
pas entre eux.
Soient Vi, p, T et ni les paramètres pour le ième gaz, V le volume total et n la quantité de matière
totale, on a alors
ii
VV
et
ii
nn
.

Chaque gaz séparé étant parfait on a : pVi = niRT. En sommant sur toutes les valeurs de i : pV = nRT.
Soit p' la pression après qu'on ait mélangé les gaz. p' = p donc p'V = nRT
C'est-à-dire que si le mélange est idéal, il constitue un gaz parfait et réciproquement.
La condition nécessaire et suffisante pour qu'un mélange de gaz parfaits ne réagissant pas entre
eux soit idéal est que ce mélange constitue lui-même un gaz parfait.
Ceci suggère qu'un gaz ne peut être parfait que si les interactions à distance entre ses molécules sont
nulles, donc si les distances entre les molécules sont grandes.
On reverra dans le cours de chimie (chapitre 2) la notion de pression partielle, la loi de Dalton, les
fractions molaires et les activités dans un mélange idéal de gaz parfaits.
22-3 Équilibre de l'atmosphère isotherme
Bien entendu, il existe un gradient de température dans l'atmosphère. Mais pour des altitudes z
comprises entre 11 km et 30 km, on peut considérer qu'elle est très grossièrement isotherme avec une
température de l'ordre de 223 K.
On assimilera d'autre part le champ de pesanteur, localement, à un champ vertical à peu près
uniforme.
On considérera aussi l'air comme étant de composition uniforme.
L'équilibre de l'atmosphère sous la seule action des forces pressantes et des forces de pesanteur se
traduit donc par l'équation locale
  gpgrad
avec
  z
ugg
, on obtient donc :
g
dz
dp 
.
En assimilant l'air atmosphérique à un gaz parfait, sa masse volumique locale est
 d
dn
M
d
dm
avec p d = dn RT donc
RT
Mp
.
On obtient donc l'équation différentielle
p
RT
Mg
dz
dp 
soit
H
dz
p
dp 
d'où
 H
z
exppp 0
km0,8
Mg
RT
H 
est la hauteur d'échelle. p0 est la pression à l'altitude z = 0.
Aux basses altitudes, un modèle mieux adapté ferait intervenir un gradient de température à peu près
uniforme :
dz
dT
de l'ordre de –7.10–3 K.m–1.
22-4 Description statistique d'un corps pur gazeux isotherme dans un champ de pesanteur uniforme,
facteur de Boltzman
Considérons un gaz parfait formé de N (très grand) molécules identiques, chacune de masse µ,
contenu dans un récipient de grande hauteur h, (z
]h;0[ 
), de section uniforme S, plongé dans le champ de
pesanteur uniforme
  z
ugg
et en équilibre thermique à la température T.
p
z
H
p0
p
z
H
p0
z
H
p0

Le raisonnement du 22-3 conduit à
 RT
Mgz
exppp 0
avec
µM N
.
En faisant intervenir la constante de Boltzman
123 K.J10.3807,1
R
k
N
, on obtient donc :
 kT
µgz
exppp 0
.
Le nombre de molécules contenues dans une tranche d'altitude z et d'épaisseur dz est :
dN(z) = N dn(z) = N p(z)
RT
d
= N S p(z)
RT
dz
=
kT
µgz
exp
RT Sp0
N
dz.
En notant
RT Sp
C0
N
=
kT
Sp0
, et
P = µgz : énergie potentielle de pesanteur d'une molécule, on a
donc
dz
kT
expC)z(dN P
.
La probabilité pour une molécule donnée de se trouver entre les altitudes z et z + dz est :
dz
kT
expK
N)z(dN
)z(dP P 
avec K =
N
C
soit
NkT
Sp
K0
.
La constante A peut aussi être retrouvée avec la condition de normation :
La probabilité pour une molécule du gaz de se trouver entre les cotes 0 et h est de 1 :
 h
0dz
kT
µgz
expK1
donc K
kT
µgh
exp1kT
µg
NkT
Sp0
d'où
kT
µgh
exp1S
Nµg
p0
.
Les molécules du fait de leur poids ont tendance à se rassembler en bas du récipient (
P basse) mais
cette tendance est contrecarrée par l'agitation thermique désordonnée qui tend à leur faire occuper tout le
récipient. Il y a donc compétition entre deux facteurs : l'énergie potentielle
P d'une molécule et une énergie
caractéristique de l'agitation thermique kT. Plus kT est grand, plus la probabilité pour une molécule d'avoir
une altitude élevée devient grande. À la limite, si T devient très grande, la pression s'uniformise dans tout le
récipient, la probabilité de trouver une molécule dans une tranche d'épaisseur dz devient indépendante de z.
Si T est très grande ou h petite devant H,
V
nRT
Sh
NkT
p0
, la pression est alors uniformément égale
à
V
nRT
.
Par définition, D(z) =
 kT expK
dz )z(dP P
est la loi de distribution des altitudes des molécules.
kT exp P
est le facteur de Boltzman et K le facteur préexponentiel.
Ce résultat ne constitue qu'un exemple d'application de la loi statistique de Boltzman.
22-5 Distribution des vitesses dans un gaz parfait, température cinétique
22-5-1 Hypothèses de la théorie cinétique des gaz parfaits monoatomiques
On considère un gaz parfait formé d'un grand nombre de molécules identiques, en équilibre
thermique et contenu dans un récipient de faible hauteur. La pression est donc pratiquement uniforme dans
ce gaz (si la température n'est pas trop basse). Ceci signifie que la densité moléculaire
RT
p
d
dn
d
dN
*n NN 
est uniforme dans ce gaz. Bien entendu, ceci devient faux si l'on considère des
"volumes élémentaires" d trop petits...