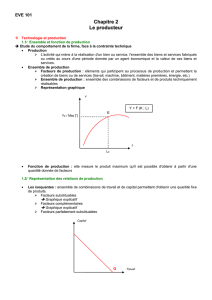
En microéconomie, l`entreprise ou le producteur se définit comme

En microéconomie, l’entreprise ou le producteur se définit comme une unité technique ou se produisent
des biens et des services (outputs) qu’elle offre sur le marché. Donc une entreprise transforme des
facteurs de production en biens et services.
On appelle facteur de production (inputs) tout bien ou service utilisé pour obtenir d’autres biens. Il existe
différents facteurs de production : les matières premières, l’énergie, les biens intermédiaires, le travail
humain, les machines et l’équipement (le capital), la formation…
Pour tous volumes de production donnée, deux questions se posent :
- Quel est le coût de ce volume de production ?
- Quelle est sa recette ?
On arrive à la notion de profit, noté
RT CT  
. Dans une économie de marché, la décision de produire
répond à l’objectif de maximisation du profit.
Or pour tout volume de production donné, le coût dépend en premier lieu de la technologie utilisé. Il
existe une contrainte technologique à laquelle fait face l’entreprise. La technologie conditionne les
quantités nécessaires des facteurs de production et les prix.
La recette de l’entreprise dépend de la demande à laquelle sera confronté l’entreprise. Il faut s’intéresser à
l’aspect technique de la production, c-a-d le choix d’une technique de production et l’aspect financier, c-
a-d les coûts de production.
Section 1 – L’approche technique de la production : Fonction de production et productivité
La quantité produite d’un bien dépend du volume de facteurs de production utilisée et de la technologie
utilisée.
I Facteur de production et fonctions de production
A – Facteur de production et distinction court terme / long terme
Les facteurs de production peuvent être ajuster plus ou moins rapidement par l’entreprise. A court terme,
une entreprise ne peut réagir pleinement à une modification de son environnement. A court terme, on
considère que certaines capacités de production sont constantes. Certains facteurs de production sont
qualifiés de fixe et certains de variables. Généralement, on considère que le facteur fixe est le facteur
capital à court terme alors que la facteur travail est variable.
A long terme, l’entreprise peut s’adapter pleinement, cela signifie que tous les facteurs de production sont
variables et il peut y avoir substitution entre les facteurs de production.
- Une entreprise installé sur un marché : cette entreprise a déjà réalisé les investissements.
- Une entreprise qui peut s’installer sur un marché : les investissements ne sont pas encore réalisé ;
la décision de produire amène à des décisions de long terme.
B – Fonction de production et contrainte technologique
On considère deux facteurs : K (quantités de facteur capital) et L (quantité de facteur travail). On peut
aussi noté x1 (quantités de facteur 1) et x2 (quantités de facteur 2).
On considère des quantités positives ou nulle de facteur de production. Donc
12
, , , 0K L x x 
.
L’expression mathématique de la relation entre quantité de bien produite et quantité de facteur de
production s’appelle la fonction de production. Donc Q = f(K ; L) ou Y = f(x1 ; x2) .
Si on considère des variations infiniment petites de bien et de facteur de production, la fonction de
production est continue et dérivable. La fonction de production dépend de la technologie : une technique
de production est une méthode particulière qui permet de combiner capital et travail pour obtenir le bien.
La technologie regroupe toutes les techniques connues pour avoir le bien. Dans l’analyse, on considère un
état donné de la technologie.
Le progrès technique permet d’introduire de nouvelles techniques de production plus productive.

La fonction de production représente la quantité maximale de bien obtenu à partir de tout volume donné
de facteur de production dans un état donné de la technologie. Elle résume toutes les techniques de
production efficientes.
Une technique de production est efficiente si on respecte le principe de non gaspillage des ressources. Si
on combine les facteurs de productions, cela signifie que pour obtenir le bien, il faut utiliser les deux.
Même s’il participe tous les deux à la fabrication du bien, ils peuvent être plus ou moins substituables.
Par contre, certains facteurs sont parfaitement complémentaires, c-a-d que la production suppose que l’on
utilise les deux facteurs dans des proportions fixes. On parle de technologie à facteur substituable et
technologie à facteur complémentaire.
On se limite au fonction de production à facteur substituable : formellement, on utilise des fonctions
Cobb – Douglas de la forme
12
( ; )Q K L K L Y x x
.
- Que se passe t’il lorsque l’on augmente l’utilisation d’un seul facteur ?
- Que se passe t’il lorsque l’on augmente l’utilisation des deux facteurs ?
II Productivité et rendement factoriel
On considère des quantités variables d’un facteur de production, l’autre supposer fixe. On appelle
productivité totale d’un facteur la quantité d’un bien pouvant être produite grâce à ce facteur.
A volume donnée de travail
kk
, la productivité totale est noté
( ; )
L
PT f k L
.
A volume donnée de capital
LL
, la productivité totale est noté
( ; )
K
PT f K L
La producitivté moyenne mesure la quantité produite par unité de facteur utilisé, l’autre supposer fixe.
Ainsi la productivité moyenne de travail est :
( ; )
LQ f K L
PM LL
Ainsi la productivité moyenne de capital est :
( ; )
KQ f K L
PM KL
Par exemple, on prend
1/2 1/2
1/2 1/2 1/2 1/2
2
22
L
Q K L
KL
PM K L
L
Donc la productivité moyenne mesure la contribution moyenne de chaque facteur à la production globale.
La productivité marginale mesure la variation de la quantité produite de bien consécutive à la variation
d’une unité de la quantité utilisée de ce facteur, l’autre demeurant constant.
Donc
L
Pm
est la dérivée de la fonction de production par rapport à L. Donc
LD
Pm L
.
Donc
K
Pm
est la dérivée de la fonction de production par rapport à K. Donc
KQ
Pm K
Reprenons l’exemple précédent :
1/2 1/2
1/2 1/2
1/2 1/2
1/2 1/2
1
22
1
22
k
L
D
Pm K L
K
KL
Q
Pm L K
L
KL

Dans un premier temps, quand on augmente la quantité d’un facteur, la productivité totale augmente à un
rythme croissant. A volume de capital donnée, augmenter le travail permet de diviser le travail donc
permet de réaliser des gains de réalisations et donc cela permet des gains de productivités. A volume de
travail donné, augmenter le capital (les machines, l’équipement) permet d’augmenter la production en
utilisant de meilleure manière le personnel.
Mais des inconvénients apparaissent et sont liés au fait qu’on utilise qu’un seul facteur de production. A
volume de capital donné, si on continue à augmenter le facteur travail, des problèmes d’organisation, de
contrôle de hiérarchie…A l’inverse, à volume de travail donné, si on continue à augmenter le capital, il
peut y avoir une sous-utilisation des machines. La productivité totale continue de progresser mais à un
rythme décroissant, c-a-d de moins en moins vite.
Si ses problèmes se poursuivent et que l’entreprise continue d’augmenter un seul facteur de production, il
peut y avoir baisse de la productivité totale du facteur considéré.
Dans la première phase (0 à 4) : Cette évolution de la productivité totale traduit la loi des rendements
factoriels décroissants. On voit que la productivité totale augmente à un rythme croissant. Donc la
productivité marginale augmente : cela signifie qu’une unité supplémentaire de facteur de production
rapporte plus que la précédente.
Dans la deuxième phase (4 à 8) : la productivité marginale diminue (une unité de facteur rapporte moins
que la précédente). La productivité totale augmente mais à un rythme décroissant.
Dans la troisième phase : la productivité totale diminue. Donc la productivité marginale devient
négative. Cela signifie que lorsque la productivité marginale est égale à 0, la productivité totale a atteint
son maximum.
Evidemment, il y a un lien entre la productivité marginale et la productivité moyenne d’un facteur. La
productivité marginale est ce que rapporte une unité supplémentaire de facteur. La productivité moyenne
est la productivité par facteur de production.
Si la productivité marginale est supérieure à la productivité moyenne, cela signifie que toute unité
supplémentaire de facteur rapporte plus que les unités précédentes déjà utilisées. Dans ce cas-là, la
productivité moyenne du facteur augmente.
Lorsque la productivité marginale est inférieure à la productivité moyenne, cela signifie qu’une unité
supplémentaire de facteur rapporte moins que les utilités déjà utilisées. Donc la productivité moyenne
diminue.
Savoir s’il est avantageux ou non d’augmenter l’utilisation d’un facteur de production, suppose que
l’entreprise compare la productivité marginale de ce facteur avec le prix de ce facteur sur le marché. Donc
productivité marginale et prix du facteur ont un lien direct avec le profit de l’entreprise puisque les
quantités utilisées de ce facteur et le prix unitaire de ce facteur de production conditionnent le coût.
Point d’inflexion de la productivité totale
Point où la productivité totale est maximum

Donc si la productivité marginale (mesuré en unité de bien produit) du facteur en valeur est supérieur au
prix du facteur de production, alors l’entreprise a intérêt à augmenter l’utilisation de ce facteur. Pour avoir
la productivité marginale en valeur, on fait référence au prix du bien sur le marché.
Si la productivité marginale en valeur est inférieure au prix du facteur de production (coût unitaire),
l’entreprise n’a plus aucun intérêt à augmenter les quantités de ce facteur. On comprend que l’entreprise
réalise des arbitrages entre les différents facteurs de production. La productivité marginale est
décroissante.
III Le choix d’une technique de production
D’une part, il faut choisir une combinaison de facteurs de production en fonction de la contrainte
technologique à laquelle l’entreprise est confrontée. La fonction de production donne les combinaisons de
facteurs qu’exige chaque technique. D’autre part, le choix d’une combinaison productive ce fait en
fonction du prix de ces facteurs de production.
On peut calculer le coût associé à chaque technique et le producteur choisit la méthode la moins coûteuse.
A – Technologie et isoquant
On s’intéresse à l’intensité d’utilisation des facteurs de production qui est relative à chaque technologie. Il
existe des secteurs d’activité à forte capitalistique (ex : secteur automobile) ; et d’autres fortement
travaillistique (ex : secteur textile).
On peut obtenir un bien avec différentes méthodes de production. Cette intensité d’utilisation est mesuré
par le rapport
K
L
(plus il est élevé, plus on utilise intensivement le capital p/r au travail).
Si deux techniques de production, l’une intensive au travail et l’autre intensive au capital permettent
d’obtenir le même volume de production, laquelle de ces deux techniques l’entreprise choisit-elle ?
Il faut déterminer l’ensemble des techniques de production qui permettent d’obtenir le même volume de
production. En microéconomie, on dispose d’un outil : l’isoquant.
Elle représente graphiquement toutes les combinaisons productives qui permettent d’obtenir le même
volume de production. On la représente dans le plan des facteurs :
Prenons deux combinaisons productives : A(KA, LA) et B(KB, LB) qui permettent le même niveau de
production, appelé
Q
. Donc on peut les relier par une courbe, l’isoquant.
L, x2
LA A C
D
LB B
KA KB K, x1
La combinaison productive A contient plus de travail et de capital que la combinaison productive B.
Donc
A
K
L
A forte intensité en travail. Donc B, le capital est relativement plus utilisé que L.
Si l’entreprise dispose d’une quantité plus élevée de facteur, elle produit plus et dans ce cas-là, on aura
une isoquant plus élevé. Donc
1
QQ
.
Par contre, quant on utilise le passage entre la combinaison productive A à la combinaison productive B,
il y a substitution des facteurs. Dans l’exemple, on augmente le capital et on diminue le travail. Comment
se réalise cette substitution entre les facteurs ?

Pour analyser cette substitution Capital / Travail, il faut analyser les déterminants de l’arbitrage entre les
facteurs à savoir :
- La productivité des facteurs
- Le prix unitaire des facteurs
Quand on considère la combinaison productive A, l’entreprise utilise relativement plus le facteur travail et
peu le facteur capital. Donc
K
L
est faible et
L
m
P
est faible mais
K
m
P
est forte. Donc l’entreprise accepte
d’augmenter le capital et de diminuer le travail. Comme la productivité marginale du capital est plus
élevé, augmenter faiblement l’utilisation du facteur capital compense une forte diminution du facteur
travail : donc au point A, l’entreprise accepte de remplacer une importante quantité de facteur travail
contre un peu de capital.
Par contre, la combinaison productive B montre une utilisation plus intensive en facteur capital qu’en
facteur travail. Dans ce cas,
K
L
est élevé,
K
m
P
est plus faible que
L
m
P
.
Dans ce cas, l’entreprise n’accepte de substituer qu’une faible quantité de travail en facteur capital. Donc
diminuer encore le travail suppose d’augmenter fortement le capital pour compenser.
Cette substitution s’analyse à travers un indicateur, le TMST (K ; L). Il mesure la quantité de facteur
travail à laquelle l’entreprise renonce pour augmenter d’une unité le facteur capital, tout en maintenant
constant le niveau de production. Donc
( ; ) 0
L
TMST K L K
. Le TMST est décroissant.
En réalité, pour procéder à cette substitution, l’entreprise compare le rendement associé à chaque facteur.
Donc
( ; ) K
L
m
m
P
TMST K L P
→ TMST A > TMST B.
Il représente ce que vaut une unité de facteur capital en terme de facteur travail. Cette substitution ne
peut avoir lieu que si capital et travail sont substituables. Si les facteurs sont strictement complémentaires,
l’entreprise ne peut arbitrer comme elle le veut entre capital et travail. La forme des isoquant reflète une
technologie à facteur substituable. En effet, nous considérons les courbes décroissante et convexe.
B – Substitution et coût des facteurs
Le coût des facteurs est le coût de l’utilisation des deux facteurs de production. On note PK le prix unitaire
du capital sur le marché et PL le prix unitaire du travail sur le marché.
Donc
KL
C p K p L   
. Donc l’entreprise, pour un niveau de production donné
Q
, recherche le coût
minimum. Pour déterminer la combinaison productive la moins coûteuse, l’entreprise va comparer ce que
lui rapporte les facteurs de production par rapport à ce qui lui coûte.
Si le coût du travail est supérieur à la productivité marginale du travail, il se peut que l’entreprise préfère
ne pas embaucher. Dans ce cas, peut être faut il substituer les facteurs. Mais ce qui compte c’est le prix
relatif c-a-d
K
L
p
p
.
Exemple :
'
'
10 15
20 22
KK
LL
pp
pp
Donc
K
L
p
p
est ce que vaut une unité de facteur capital en terme de facteur travail sur le marché des facteurs
de production. C’est le taux d’échange des facteurs de productions.
Exemple : à prix du capital et du travail donnée, l’entreprise compare ce que coûte les deux facteurs sur le
marché. Si le prix du travail augmente de 5% et le prix du capital augmente de 10%, l’entreprise préfère
embaucher et préfère utilisée des combinaisons productives plus intensives en travail car le prix relatif du
travail a baissé.