Modèle mathématique.

Complexes
EXERCICE 1
Le plan est muni d’un repère (O ;
Error!
,
Error!
). A tout point M d’affixe z non nul on associe
le point M’ d’affixe z’= -
Error!
.
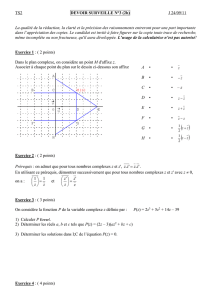
1. Construire les images des points A d’affixe a=1+i et B d’affixe b=2i.
2. On pose z=x+iy et z’=x’+iy’.
a. Exprimer x’ et y’ en fonction de x et y.
b. En déduire que O, M et M’ sont alignés.
3. Montrer que
)1(
1
1'  z
z
z
4. On note C et D les points d’affixes 1 et -1. * le cercle de centre C, passant par O
et privé de O. On suppose que M *.
a. Justifier que
11 z
et montrer que
'1' zz 
. Interpréter géométriquement
cette relation.
b. En déduire une construction de M’ à partir de M.
EXERCICE 2
Dans le plan complexe rapporté au repère orthonormal direct (O ;
Error!
,
Error!
) d’unité
graphique 4 cm, on considère les points A, B et C,
d’affixes a, b et c telles que : a = 1−i , b = 1+i et c = −1+i = −a
On note  le cercle de diamètre [AB].
1. a) Placer sur une figure les points A, B, C et le cercle .
b) Mettre les nombres complexes a, b et c sous forme trigonométrique.
c) Soit r la rotation de centre O telle que r (A) = B.
Déterminer l’angle de r et le point r (B), image de B par r.
d) Déterminer l’image ’ du cercle  par r ; placer ’ sur la figure.
2. On considère un nombre ]0, [ ];2 [ ; on note M le point d’affixe z = 1+ei 
On désigne par M’′ l’image de M par r, et on appelle z′ l’affixe de M’.
a) Montrer que M est un point de  distinct de A et de B.
b) Exprimer z′ en fonction de z.
Calculer en fonction de les affixes u et u′ des vecteurs
Error!
et
Error!
.
c) Etablir la relation :
u= u’ tan(
Error!
-
Error!
)
d) Prouver que les points B, M et M’ sont alignés.
Placer sur la figure un point M et son transformé M’.
EXERCICE 2
Le plan est muni d’un repère orthonormal (O ;
Error!
,
Error!
) . On prendra 2 cm pour unité
graphique.
On considère l’application F du plan dans lui-même qui, à tout point M d’affixe z, associe
le point M’′ d’affixe z′ tel que : z′ = (1+i)z +2
1. Soit A le point d’affixe zA = −2+2i .
Déterminer les affixes des points A′ et B vérifiant respectivement :
A′ = F(A) et F(B) = A.
2. Construction de l’image de M

a) Montrer qu’il existe un unique point invariant (confondu avec son image) dont l’affixe
est 2i ; on notera  ce point et son affixe.
b) Établir que, pour tout nombre complexe z distinct de ,
Error!
= -i .
Soit M un point distinct de . Comparer MM’ et M et déterminer une mesure de
l’angle (
Error!
,
Error!
). En déduire une
méthode de construction de M’ à partir de M.
3. Image d’un ensemble de points
a) Déterminer la nature et les éléments caractéristiques de l’ensemble  des points du
plan dont l’affixe z vérifie |z+2−2i | = 2.
Vérifier que B est un point de .
b) Démontrer que, pour tout nombre complexe z : z’+2= (1+i ) (z +2−2i )
Démontrer, en utilisant cette égalité et la question 3a que l’image par F de tout point de
 appartient au cercle ’ de centre A′ et de rayon 2. Placer  , A, B, A’,  et ’ sur une
même figure.