Document

P a g e | 1
Le Jokari Document : M.Moppert - CPF - Beyrouth
TS
Physique
Le Jokari
Exercice résolu
Enoncé
Par un beau dimanche de printemps, Spirou et Fantasio (deux personnages de bande dessinée), en vacances au
Pays Basque (région de la France et de l’Espagne), décident d’aller jouer au Jokari sur la place du petit village
d’Ustaritz (en France). Le Jokari, ancien jeu de raquettes basque, est constitué d’un support en bois lesté, fixe,
auquel est accroché un élastique. A l’autre extrémité de l’élastique est accrochée une petite balle en mousse. Le
joueur a en main une raquette en bois, appelée pala, avec laquelle il frappe la balle (voir schéma ci-dessous).
Lorsque la balle rebondit au sol, elle repart vers l’arrière et le joueur peut à nouveau la frapper. L’avantage d’un
tel jeu est de pouvoir jouer à la pelote basque sans avoir de fronton (mur) à sa disposition.
Fantasio a filmé Spirou pendant qu’il jouait. Ils ont ensuite tous les deux exploité le film à l’aide d’un logiciel
adapté. Ils ont obtenu la chronophotographie des positions du centre d’inertie G de la balle, donnée en annexe
n°3 (échelle : 5,0 cm sur l’enregistrement représentent 1,0 m dans la réalité). À la date t0 = 0, la balle est
supposée être sur le support en O : elle est frappée à cet instant.
Données :
 Longueur à vide de l’élastique : l0 = 4,0 m
 Constante de raideur de l’élastique : k = 0,80 N.m-1
 Lorsque l’élastique est tendu et que sa longueur est l, il
exerce une force de rappel de valeur : F = k.(l - l0)
 Masse de la balle : m = 50 g
 Valeur du vecteur champ de pesanteur : g = 10 m.s-2
 La caméra numérique enregistre 25 images par seconde, ce qui
correspond à une durée = 40 ms entre deux images
successives.
 Contrairement au dessin ci-contre, lorsque l’élastique est tendu, il est rectiligne.
 Tous les frottements sont négligés
A. Première partie : étude cinématique
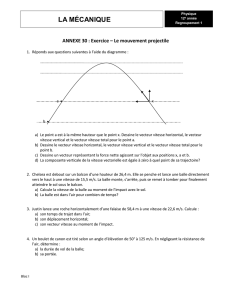
1. Par simple observation de la chronophotographie en annexe, donner des informations sur la nature du
mouvement pendant la phase de montée et pendant la phase de descente de la balle.
2. Montrer qu’à la date t20, l’élastique commence à se tendre.
3. Déterminer les valeurs v25 et v27 des vecteurs vitesse aux dates t25 et t27.
4. Construire les vecteurs vitesse
25
v
et
27
v
aux dates t25 et t27 (échelle : 1,0 cm pour 1,0 m.s-1).
5. Construire, à la date t26, le vecteur
26 27 25
v v v  
6. En déduire la valeur a26 du vecteur accélération à la date t26.
7. Construire le vecteur accélération
26
a
(échelle : 1,0 cm pour 10 m.s-2).

P a g e | 2
Le Jokari Document : M.Moppert - CPF - Beyrouth
B. Deuxième partie : étude dynamique
1. Dans le référentiel terrestre supposé galiléen, faire le bilan des forces extérieures qui s’exercent sur la
balle à la date t26 (tous les frottements sont négligés).
2. Calculer les valeurs de chacune de ces forces, et les représenter sur la chronophotographie en annexe
(échelle : 1,0 cm pour 1,0 x 10-1 N).
3. Déterminer graphiquement le vecteur
R
résultante des forces.
4. La deuxième loi de Newton est-elle vérifiée à la date t26 ?

P a g e | 3
Le Jokari Document : M.Moppert - CPF - Beyrouth
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
20
21
24
25
26
27
28
29
30
31
32
33
34
19
23
22
Annexe

P a g e | 4
Le Jokari Document : M.Moppert - CPF - Beyrouth
Corrigé
A. Première partie : étude cinématique
1. Par simple observation de la chronophotographie en annexe, donner des informations sur la nature du mouvement pendant la phase
de montée et pendant la phase de descente de la balle.
Pendant la phase de montée, la valeur de la vitesse diminue (la distance parcourue entre deux enregistrements
successifs diminue) : le mouvement de G est donc curviligne retardé. Pendant la phase de descente, la valeur de
la vitesse augmente (la distance parcourue entre deux enregistrements successifs augmente) : le mouvement de
G est donc curviligne accéléré.
2. Montrer qu’à la date t20, l’élastique commence à se tendre.
A la date t = t20, la distance OG20 est égale à 20,2 cm soit 4,0 m dans la réalité, ce qui correspond à la longueur
à vide de l’élastique. À une date t < t20, l’élastique n’est pas tendu : OG < l0. À une date t > t20, l’élastique est
tendu : OG > l0.
3. Déterminer les valeurs v25 et v27 des vecteurs vitesse aux dates t25 et t27.
On assimile vecteur vitesse instantanée à la date ti avec vecteur vitesse moyenne entre les dates ti-1 et ti+1
encadrant ti et proches de ti. Dans ces conditions :
i 1 i 1 i 1 i 1
i
i 1 i 1
G G G G
vt t 2
et vi =
i 1 i 1
GG
2
On a alors : v25 =
24 26
GG
2
et v27 =
26 28
GG
2
(on mesure 1,9 cm pour G24G26 et 2,1 cm pour G26G28)
Soit : v25 =
3
1,9 0,20
2 40 10
= 4,8 m.s-1 et v27 =
3
2,1 0,20
2 40 10
= 5,3 m.s-1
4. Construire les vecteurs vitesse
25
v
et
27
v
aux dates t25 et t27 (échelle : 1,0 cm pour 1,0 m.s-1).
Voir schéma en fin de corrigé.
5. Construire, à la date t26, le vecteur
26 27 25
v v v  
Voir schéma en fin de corrigé.
6. En déduire la valeur a26 du vecteur accélération à la date t26.
On assimile vecteur accélération instantanée à la date ti avec vecteur accélération moyenne entre les dates ti-1
et ti+1 encadrant ti et proches de ti.
Dans ces conditions :
1 i 1
i
i 1 i 1
i
vv
att
i
v
2
et ai =
i
v
2
On a alors : a26 =
27 25
vv
2
soit : a26 =
3
1,3
2 40 10
= 16 m.s-2 (on mesure 1,3 cm pour
i
v
)
7. Construire le vecteur accélération
26
a
(échelle : 1,0 cm pour 10 m.s-2).
Voir schéma en fin de corrigé.

P a g e | 5
Le Jokari Document : M.Moppert - CPF - Beyrouth
B. Deuxième partie : étude dynamique
1. Dans le référentiel terrestre supposé galiléen, faire le bilan des forces extérieures qui s’exercent sur la balle à la date t26 (tous
les frottements sont négligés).
-
P
: poids de la balle.
-
T
: force de rappel de l’élastique.
2. Calculer les valeurs de chacune de ces forces, et les représenter sur la chronophotographie en annexe (échelle : 1,0 cm
pour 1,0 x 10-1 N).
P = m.g soit : P = 50 x 10-3 x 10 = 5,0 x 10-1 N
T = k.(OG26 – l0) soit : T = 0,80 x ((22,7 x 0,20) – 4,0) = 4,3 x 10-1 N (on mesure 22,7 cm pour OG26)
Voir schéma en fin de corrigé pour la représentation.
3. Déterminer graphiquement le vecteur
R
résultante des forces.
Voir schéma en fin de corrigé.
On trouve : R = 8,0 x 10-1 N (on mesure 8,0 cm pour
R
)
4. La deuxième loi de Newton est-elle vérifiée à la date t26 ?
Si la deuxième loi de Newton est vérifiée, on doit avoir :
P
+
T
=
R
= m.
26
a
On constate sur le schéma que
R
et
26
a
sont colinéaires et de même sens.
De plus m.a26 = 50 x 10-3 x (1,6 x 10) = 8,0 x 10-1 N
La deuxième loi de Newton est vérifiée à la date t26.