car0401M - Académie de Poitiers

A C A D E M I E D E P O I T I E R S Session 2001
Examen :
Brevet Professionnel Carrosserie Construction Maquettage
Coef :
2
Durée
2 H 00
Epreuve :
M a t h é m a t i q u e s
Feuille 1/6
1/6
ATTENTION
LES ANNEXES 1 ET 2 SONT A REMETTRE AVEC LA COPIE D’EXAMEN
EXERCICE : Distance d’arrêt d’un véhicule.
La distance d’arrêt d’un véhicule d, exprimée en mètres, (distance entre le moment où le conducteur voit un
obstacle et l’arrêt du véhicule) est donnée en fonction de la vitesse v, en km/h par la relation :
d = 0,007 v2 + 0,8 v
1 – Calculer d (arrondie à l’unité) lorsque v = 90 km/h.
2 – a) Calculer les vitesses (arrondies à l’unité) pour lesquelles la distance d’arrêt est 50 m, puis 100 m.
b) La distance d’arrêt d’un véhicule est-elle proportionnelle à la vitesse ? Justifier.
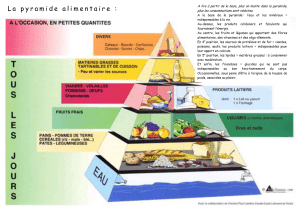
PROBLÈME : Étude d’un réservoir à eau.
La figure 1 (non représentée à l’échelle) est le schéma d’un réservoir à eau. Il est composé d’une pyramide
régulière à base carrée, IJKL, de sommet S surmonté d’un pavé droit.
SB
est la hauteur du réservoir.
SA
est la hauteur de la pyramide.
SI
est l’arrête de la pyramide.
Le réservoir se vide par une vanne située en S.
On donne : SB = 13,0 m
IJ = 6,0 m
SI = 6,5 m
On considère le plan de symétrie
P
contenant N milieu du segment
IL
Première partie.
1 – a) Calculer la mesure du segment
AI
b) Calculer la hauteur de la pyramide
SA
à l’unité près.
2 – Représenter, sur l’annexe 1, la coupe longitudinale suivant le plan
P
en utilisant l’échelle 1/100.

A C A D E M I E D E P O I T I E R S Session 2001
Examen :
Brevet Professionnel Carrosserie Construction Maquettage
Coef :
2
Durée
2 H 00
Epreuve :
M a t h é m a t i q u e s
Feuille 2/6
2/6
Deuxième partie
1 – Calculer le volume V1 de la pyramide au m3 près.
2 – Calculer le volume V2 du pavé droit au m3 près.
3 – En déduire le volume total du réservoir.
Troisième partie
Sachant que le réservoir t plein contient 348 m3 d’eau, et qu’il faut 10 heures pour le vider :
- Quelle est en m3 / h le débit volumique, supposé constatant, au niveau de la vanne ?
- Convertir en L / min.
Dans la quatrième et cinquième partie, on considère :
- SA = 5 m.
- SH = x où H est un point appartenant au segment
SB
.
Quatrième partie : 0  x  5
Pour 0  x  5, le point H se situe entre S et A. On exprime alors le volume V1
x
d’eau contenu dans le
réservoir en fonction de la hauteur x d’eau par la relation :
3
125
12
Vxx 
1 – Calculer : V1
0
; V1
1
; V1
2
; V1
3
; V1
4
; V1
5
puis reproduire et compléter le
tableau suivant
Points
M0
M1
M2
M3
M4
M5
Abscisses x (en m)
0
1
2
3
4
5
Ordonnées V1
x
(en m3)
2 – Placer les points M1, M2 , M3 et M4 dans le repère figurant en annexe 2 et tracer la courbe passant par
ces points.

A C A D E M I E D E P O I T I E R S Session 2001
Examen :
Brevet Professionnel Carrosserie Construction Maquettage
Coef :
2
Durée
2 H 00
Epreuve :
M a t h é m a t i q u e s
Feuille 3/6
3/6
3 – Que représente V1
5
?
4 – On se propose dans cette question de calculer le volume d’eau pour x = 2,5 m à l’aide de trois méthodes.
a) Déterminer graphiquement V1
5,2
.
b) Calculer V1
5,2
.
c) On appelle le point E, le milieu du segment
JK
. Représenter les points E et H sur le schéma en
coupe en annexe 1 puis tracer la parallèle à
AE
passant par H, qui coupe le segment
SE
en C.
A l’aide du théorème de Thalès, retrouver V1
5,2
en calculant le volume de la pyramide
correspondant.
Cinquième partie 5  x  13
Pour 5  x  13 le point H se situe maintenant entre A et B.
Soit V2
x
le volume d’eau en fonction de la hauteur d’eau.
1 – Que représente V2
5
?
2 – Calculer le volume d’eau si la hauteur d’eau x = 10 m.
3 – Déterminer V2
x
, le volume d’eau, en fonction de x, la hauteur d’eau.
4 – Reproduire et compléter le tableau suivant :
Points
M5
M7
M8
M9
M11
M12
Abscisses x (en m)
5
7
8
9
11
12
Ordonnées V2
x
(en m3)
Placer les points M5, M7, M8, M9, M11, M12 dans le repère figurant en annexe 2 et tracer la courbe passant par
ces points.
5 – Lire graphiquement la valeur du volume total du réservoir. Que remarquez-vous ?
Barème : Exercice : 4 points
Problème : 16 points.

ANNEXE 2 À REMETTRE AVEC LA COPIE
4/6

ANNEXE 2 À REMETTRE AVEC LA COPIE
5/6
V
x
(en m3) REPRÉSENTATION GRAPHIQUE
x (en m)
1
2
4
5
6
12
10
9
11
3
7
8
120
140
160
200
220
240
260
280
300
340
0
20
60
40
80
100
180
320
360
380
400