Statistiques (approches théorique et logicielle) Licence STAPS 2è

Statistiques (approches théorique et logicielle)
Licence STAPS 2è année (L2)
UFR STAPS de NICE Année Universitaire 2007 / 2008
1
Imed ben Mahmoud
Chapitre 3
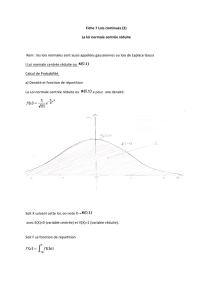
La loi normale
Le modèle normal
La loi normale est fondamentale dans le domaine de la statistique. Une multitude de
phénomènes associés à des variables continues correspondent à cette loi ou du moins peuvent
être approximés convenablement. Le graphique de la distribution normale se présente sous
forme de cloche et la courbe résultante est appelée courbe normale.
L'expression mathématique de cette distribution de probabilités fut d'abord publiée par
Abraham LeMoivre en 1733. D'autres théoriciens sont également associés à cette fameuse loi,
soit le Marquis de Laplace (1667-1754) et Carl Friedrick Gauss (1777-185).
C'est pour cette raison qu’on trouve également dans la littérature les termes distribution
gaussienne ou distribution de Laplace-Gauss ou simplement loi normale. Elle jouit d'une
importance fondamentale puisqu'un grand nombre de méthodes statistiques reposent sur cette
loi. Les applications associées à cette loi sont également très nombreuses.
Distributions normales Distributions normales
ayant le même écart-type ayant la même moyenne
mais de moyennes différentes mais d’écarts-types différents
1 = 2 , m2 > m1 m2 = m1 , 1 = 2
m1 m2
m2 > m1 m1 = m2
Propriétés importantes de la loi normale
- La courbe normale est une distribution statistique théorique et la caractéristique X
qui obéit à cette distribution peut prendre toutes les valeurs entre -  et +  .
- L'aire sous la courbe normale et l'axe horizontal correspond à une fréquence relative
de sorte que l'aire totale correspond à 1 (ou 100%).
- Le graphe de la courbe normale est symétrique par rapport à la droite d'abscisse m
(la moyenne). Par conséquent 50% de l'aire se situe à la gauche de m et 50% à la droite.
- La distribution normale étant unimodale et symétrique, on a
moyenne = médiane = mode
- Pour toute distribution normale de moyenne m et d'écart-type , on peut affirmer que
68,26% des données se situent dans l'intervalle [m - 1, m +1].
95,44% des données se situent dans l'intervalle [m - 2, m + 2].
99.74% des données se situent dans l'intervalle [m - 3, m + 3].

Statistiques (approches théorique et logicielle)
Licence STAPS 2è année (L2)
UFR STAPS de NICE Année Universitaire 2007 / 2008
2
m - 2 m m + 2
m - 3 m - 1 m + 1 m + 3
Courbe normale centrée réduite
Ainsi dans le cas d'une variable aléatoire normale, 95% des valeurs de la variable sont
comprises entre m - 1,96  et m + 1,96 , alors que pratiquement 99% des valeurs sont
comprises entre m - 2,58  et m + 2,58 .
Variable centrée réduite et loi normale
L'aire qu'on peut obtenir sous la courbe normale permet d'évaluer les chances sur 100, ou
encore la probabilité que la valeur éventuelle d'une variable aléatoire normale se situe entre
deux valeurs données, ou encore qu'elle soit supérieure ou inférieure à une valeur particulière.
Pour faciliter ce calcul, on a recours à une table standardisée qui permet d'obtenir l'aire sous
la courbe normale, peu importe les valeurs de m et/ou . Il faut toutefois transformer la
variable X en une variable centrée réduite, variable qui ne comporte aucune unité de mesure.

Statistiques (approches théorique et logicielle)
Licence STAPS 2è année (L2)
UFR STAPS de NICE Année Universitaire 2007 / 2008
3
Variable centrée réduite : soit X, une variable aléatoire continue, distribuée selon une loi
normale de moyenne m et de variance ². La variable Z, obtenue de la transformation :
Z = (X-m)/
m-2 m m+2 -3 -2 -1 0 +1 +2 +3
m-3 m-1 m+1 m+3
Utilisation de la table de la normale centrée réduite
Avant de présenter un contexte d'application de la loi normale, indiquons comment obtenir
l'aire sous la courbe normale centrée réduite à l'aide des valeurs de la table de la loi normale
centrée réduite.
Précisons d'abord que la table de la loi normale centrée réduite ne donne que l'aire
(probabilité) sous la courbe pour des valeurs positives de Z. Toutefois, puisque la courbe est
symétrique par rapport à zéro:
L'aire sous la courbe entre 0 et Z1 est notée P(0 < Z < Z1).
Détermination de l'aire sous la courbe normale centrée réduite
a) Cherchez P(0 < Z < 0,5).
On veut l'aire sous la courbe normale centrée réduire entre Z = 0 et Z = 0,5. Pour facilité le
raisonnement, traçons la courbe en mettant en relief l'aire cherchée.
Pour trouver l'aire cherchée, on fait usage de la table de la loi normale centrée réduite, dont
nous reproduisons ici une partie. Donc pour Z = 0,5, on lit directement de la table, 0, 1915.
Donc, dans le cas d'une variable centrée réduite, on peut dire qu'un peu plus de 19% des
valeurs se situent entre 0 et 0,5.

Statistiques (approches théorique et logicielle)
Licence STAPS 2è année (L2)
UFR STAPS de NICE Année Universitaire 2007 / 2008
4
A cause de la symétrie de la loi normale centrée réduite, ceci donne également (indiquez la
valeur appropriée)
P(-0,5  Z  0) = 0,1915
b) Déterminez P(-2,24 < Z < 1,12). On cherche l'aire sous la courbe normale centrée réduite
entre Z = -2,24 et Z =1,12.
Esquissons d'abord la courbe normale centrée réduite et indiquons l'aire cherchée.
A Z = 1,12 correspond 0,3686 (ce qui donne P(0  Z  1,12)).
A Z = 2,24 correspond 0,4875 (ce qui donne P(0  Z  2,24) = P(-2,24  Z  0)). Par
conséquent, l'aire cherchée correspond à la somme suivante:
Pratiquement 86% des valeurs d'une variable centrée réduite se situent entre -2,24 et 1,12.
c) Détermination de la valeur de la variable centrée réduite pour une aire donnée.
On demande de déterminer le nombre k tel que 42,36% des valeur, de la variable centrée réduite
se situent entre 0 et k soit P(0 < Z < k) = 0,4236.
Il s'agit d'abord de localiser dans la table da la loi normale centrée réduite, l'aire donnée et de
déterminer la valeur Z correspondante.

Statistiques (approches théorique et logicielle)
Licence STAPS 2è année (L2)
UFR STAPS de NICE Année Universitaire 2007 / 2008
5
Ainsi à 0,4236, qui correspond à l'aire entre 0 et k, on trouve directement k =1,43.