1) - Comment modéliser la trajectoire d`un obus

3ème PARTIE : MODELISATION DE
L’ATTRACTION TERRESTRE ET DE LA TRAINEE
AERODYNAMIQUE
1) Définitions :
Dans le cadre de cette modélisation:
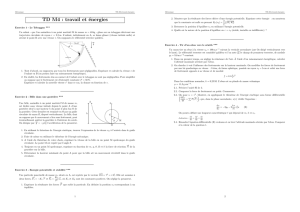
 L’obus est assimilé à un point matériel M, de masse constante m
 Il est soumis à l’attraction terrestre et à la résistance aérodynamique
 Le référentiel est un référentiel terrestre local :
 Son origine se situe à la bouche du canon, c’est-à-dire au point où l’obus
commence sa trajectoire soumise uniquement à l’attraction terrestre
 Son axe
z
O
est défini selon la verticale locale ascendante
 Son axe
x
O
est défini suivant l’horizontale locale ; il est orienté selon le
vecteur vitesse initiale, c’est-à-dire que le plan (Ox, Oz) contient la
direction de tir
 Son axe
y
O
complète le repère pour en faire un repère direct
 Ces axes sont munis d’un repère orthonormé direct (O, i, j, k)
 Ceci revient à considérer que la Terre est plate, ce qui n’est acceptable qu’à
faible échelle (on le verra par la suite).
 Ce référentiel est considéré comme galiléen ; nous en étudierons plus loin
les limites.
Ceci revient à considérer que l’obus est un point matériel de masse constante se
déplaçant dans un référentiel approximativement galiléen sur une Terre plate.
2) Notations
Dans ce repère :
 Les coordonnées du point M sont notées x, y, z : OM = xi + yj + zk
 La vitesse du point M est notée V, et ses composantes sont notées
x
V
,
y
V
,
z
V
:
V =
d(OM)
dt
=
x
V
i +
y
V
j +
z
V
k , avec
x
V
=
dx
dt
,
y
V
=
dy
dt
,
z
V
=
dz
dt
 L’accélération du point M est notée A, et ses composantes sont
x
A
,
y
A
,
z
A
:
A =
d²(OM)
dt²
=
x
A
i +
y
A
j +
z
A
k, avec
x
A
=
d²x
dt²
,
y
A
=
d²y
dt²
,
z
A
=
d²z
dt²
A t=0, l’obus est tiré avec une vitesse initiale Vo et un angle de site  :
 = angle (
x
O
, V)

3) Modélisation
Selon la deuxième loi de Newton :
« Dans un référentiel galiléen, la force qui s’exerce sur un point matériel est égale à la dérivée
par rapport au temps du vecteur quantité de mouvement. »
F=
dp
dt
, avec p=mv=m
dx
dt
Comme la masse en mouvement est constante dès la sortie de la bouche du canon, la dérivée
par rapport au temps du vecteur quantité de mouvement vaut:
dp
dt
=
d(mv)
dt
= m
dv
dt
et comme v =
d(OM)
dt
dp
dt
=
d(mv)
dt
= m
d²(OM)
dt²
soit finalement:
F =
²)²( dt
OMd
m
Enoncé des forces
L’obus est soumis :
 à la gravité, donc F1 = mg , avec g orienté selon la verticale descendante.
 à la résistance de l’air F2, orientée selon V et de sens opposé. Son module vaut :
F2 = ½  S Cx f(V), où :
 est la masse volumique de l’air
S est la surface frontale de l’obus
Cx est le coefficient de traînée
f(V) est une fonction du module de V
V est la vitesse par rapport à la masse d’air
Une expression vectorielle de F2 est :
F2 = - ½  S Cx f(V)
V
/ V
Influence du vent
Par simplification, le vent W est supposé ne varier qu’avec l’altitude z
1
. Il est assimilé à une
vitesse horizontale W = (
x
W
,
y
W
).
L’obus se déplace alors dans un repère aérodynamique (O’x’y’z’) :
 dont les axes sont parallèles aux axes du repère (Oxyz)
 dont l’origine est animé d’une vitesse constante W(z) par rapport à l’origine O.
1
Dans la réalité, le vent peut avoir une composante verticale, parfois marquée localement, et une composante
horizontale qui varie selon le lieu. Ainsi, on peut avoir un vent d’Ouest de 10 m/s à Paris, et un vent du Sud-
Ouest de 20 m/s à Laon.

Selon le principe fondamental de la dynamique du point matériel, , la vitesse de l’obus dans le
trièdre (Oxyz) est égale à la vitesse de l’obus dans le trièdre (O’x’y’z’) augmentée de la
vitesse du trièdre (O’x’y’z’) par rapport au trièdre (Oxyz)
2
:
Vx= Vx’ + Wx
Vy = Vy’ + Wy
Vz = Vz’
De ce fait, la résistance de l’air devient, avec l’égalité vectorielle V’ = V – W :
En projection dans le trièdre Oxyz :
La force F1 se projette uniquement suivant Oz. La force F2 se projette suivant Ox et Oz :
F2x = ½  S Cx f(V’) Vx/ V’
F2 z= ½  S Cx f(V’) Vz/ V’
Alors
Ax = m d²x/dt² = F2x = ½  S Cx f(V’) Vx/ V’ (1)
Ay = m d²y/dt² = 0 (2)
Az = m d²z/dt² = m g + F2z = ½  S Cx f(V’) Vz/ V’ (3)
Vx = Vx’ + Wx
Vy = Vy’ + Wy
Vz = Vz’
Conditions initiales :
Par hypothèse, on a lorsque t=0 : x = 0
y = 0
z = 0
x
V
= Vo cos()
Vy = 0
Vz = Vo sin()
4) La trajectoire est plane :
En l’absence de composante de vent selon Oy, la trajectoire est entièrement contenue dans le
plan (Ox, Oz). En effet, comme Vy = 0 et Ay = 0, y est constant à tout instant. Or, à t = 0, y =
0. Donc :
y = 0 pour tout t
Dorénavant, on ne travaillera que dans le plan (Ox, Oz).
2
Cette vitesse est appelée vitesse d’entraînement du trièdre O’x’y’z’ par rapport au trièdre Oxyz. Elle est
constante dans notre cas.
V' / 'V )f(V'Cx S 1/2 - F2 

5) Les effets de l’atmosphère
a) Le vent W
Le vent peut avoir une influence certaine. Supposons qu’il s’applique sur une toute une
trajectoire qui dure 3 minutes ( = 180 secondes, valeur typique). Alors l’écart à l’arrivée sera
180 * W, soit 1800 m pour une erreur de 10 m/s.
Ceci mérite d’être nuancé, car l’obus du canon de Guillaume traversait les couches basses de
l’atmosphère, puis les couches hautes, puis sortait presque de l’atmosphère. Si dans les
couches basses le vent atteint couramment 20 m/s, il atteint 100 m/s vers 7000 m, et disparaît
vers 30000 m. Il est bien entendu concevable de corriger le vent en fonction du vent mesuré
par sondage (encore que ces techniques ne soient pas encore disponibles en 1918), mais
l’impact de l’erreur de mesure reste néanmoins.
b) La masse volumique  (atmosphère standard) :
On ne peut tenir compte des caractéristiques de l’atmosphère à tout instant et en tout lieu.
Pour la représenter du mieux possible à différentes altitudes, on a définie une atmosphère
standard.
La définition d’une atmosphère standard repose sur les conventions suivantes :
 L’air est un gaz parfait, qui vérifie : PV =  R T, avec R = 287,053 J/kgK
 La distribution verticale de la pression obéit à la loi d’équilibre hydrostatique :
dP = -  g dz
L’atmosphère standard est divisée en 7 couches s’étendant du niveau de la mer jusqu’à 86 km
d’altitude. La détermination d’une loi de tempétaure en fonction de l’altitude te celle d’une
pression au niveau de la mer déterminent alors la loi altitude-pression. Par définition, la loi de
température est : T = Tb + λ (z – zb).
Zb (km)
Z (km)
Tb (K)
λ (°K/km)
0
11
288.15
-6.5
11
20
216.65
0
20
32
216.65
1
32
47
228.65
2.8
47
51
270.65
0
51
71
270.65
-2.8
71
86
214.946
-2
Par intégration, on obtient : P = Pb ( 1 + λ (z – zb) / Tb) – g / λ R
D’où l’on déduit : ρ = P / R T = Pb ( 1 + λ (z – zb) / Tb) – g / λ R / R T, avec ρo = 1.225 kg/m2
On constate que la formulation mathématique n’est pas simple.
6) Modélisation de la traînée :
a) Le coefficient de traînée Cx :

Ce coefficient dépend de la forme de l’obus. Il est déterminé par analyse des éléments
contributifs (pointe, culot, etc) chacun ayant une contribution fournie dans des tables. Une
simulation numérique est aussi possible. Enfin, on prend en compte les résultats des
expériences.
b) La fonction f(V) :
Cette fonction est, comme Cx, déterminée expérimentalement. Elle peut être approchée sous
différentes formes :
 tables de valeurs numériques
 f(V) = k Vn . Des tables donnent k et n. Cette forme se prête bien à des résolutions
analytiques.
 f(V) = [0.222 V - 48.05 + ((0.1648 V – 47.95)² + 9.6)½ + 0.0442 V ( V –300) / (371 +
(V / 200) 10 )] 10-2 . Cette formule, établie par Siacci
3
, est largement utilisée. Son
domaine de validité s’étend de 0 à 1200 m/s. Faute d’avoir trouvé une formule ayant
un meilleur domaine de validité, nous l’utiliserons.
7) Intégration numérique :
a) Formulation :
Equations différentielles :
m d²x/dt² = ½  S Cx f(V)
x
V
/ V (1)
m d²z/dt² = m g + ½  S Cx f(V) Vz/ V (3)
Conditions initiales : à t = 0 :
x
V
= Vo cos()
Vz = Vo sin()
x = 0
z = 0
b) Résolution analytique :
Il n’y a pas de résolution analytique possible.
c) Résolution numérique :
Bien que la forme des équations soit sensiblement plus complexe que dans le modèle à
gravité seule, on peut appliquer exactement les mêmes méthodes. Toutefois, la
complexité du tableau Excel explose, puisqu’il faut à chaque pas intermédiaire
3
Officier et mathématicien italien, 1839-1907.